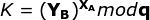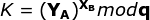Diffie-Hellman密钥交换

原 作者 朱新全 | 发表于 | 分类于 2014级

上篇说到了RSA公钥加密算法，这里看一下D-H密钥交换。

首先我们看一下数学上的概念：

本原根：我们定义素数p的本原根为其乘方能够产生从1到p - 1的所有整数的数

比如：若a是素数p的本原根，那么下列数字：

a mod p， a^2 mod p ，…… ，a^(p - 1) mod p

是互不相同的数字， 并且以某种排列包含了从1～p - 1的所有整数。也就是说，对于任何小于 p 的整数 b 和 素数 p 的本原根来说，都有唯一一个指数i满足：

b = a^i mod p   其中0 <= i <= (p - 1)

好了，更加深入的数学自行学习，我们和学习RSA一样，先来开一下D-H密钥交换中使用的几个值：

  1. XA ：用户A选择的一个小于q随机整数（用户A私有）
  2. XB ：用户B选择的一个小于q随机整数（用户B私有）
  3. YA ：用户A计算出来的供对方使用的公有值
  4. YB ：用户B计算出来的供对方使用的公有值

在这个方案中，素数q和q的本原根整数α 是两个众所周知的数字，密钥的生成过程如下：

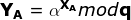
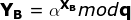
假设有两个用户A和B，首先A选择一个随机的并且小于q的整数 XA 并且计算这里写图片描述 。B用户也随机选择一个小于q的整 XB 并且计算这里写图片描述。这样就得到了 YA 和 YB ，也就是A和B的公有值， XA 和 XB 对应 A和B的私有值。

这样有了公有值 YA ， YB ，然后双方交换 YA ， YB 给对方，然后用户A和用户B根据传过来的值计算他们要使用的密钥值，计算的公式如下：

===========================

！！！很重要！！！

这里写图片描述

这里写图片描述

这里写图片描述

这里写图片描述

===========================

根据上述四个公式可以在数学上严密的知道A用户和B用户计算出来的K值是相同的（数学公式自行推导），与此同时，在网络传输的过程中并没有K值的泄露，在网络上进行传输的只有素数q和q的本原根整数α以及相互交换的 YA 和 YB ，根据这四个值是无法推测出K的值的，所以D-H密钥交换也是比较安全的。