level_5.1
关卡链接:level_5.1
本小关的目的是让大家了解规则。
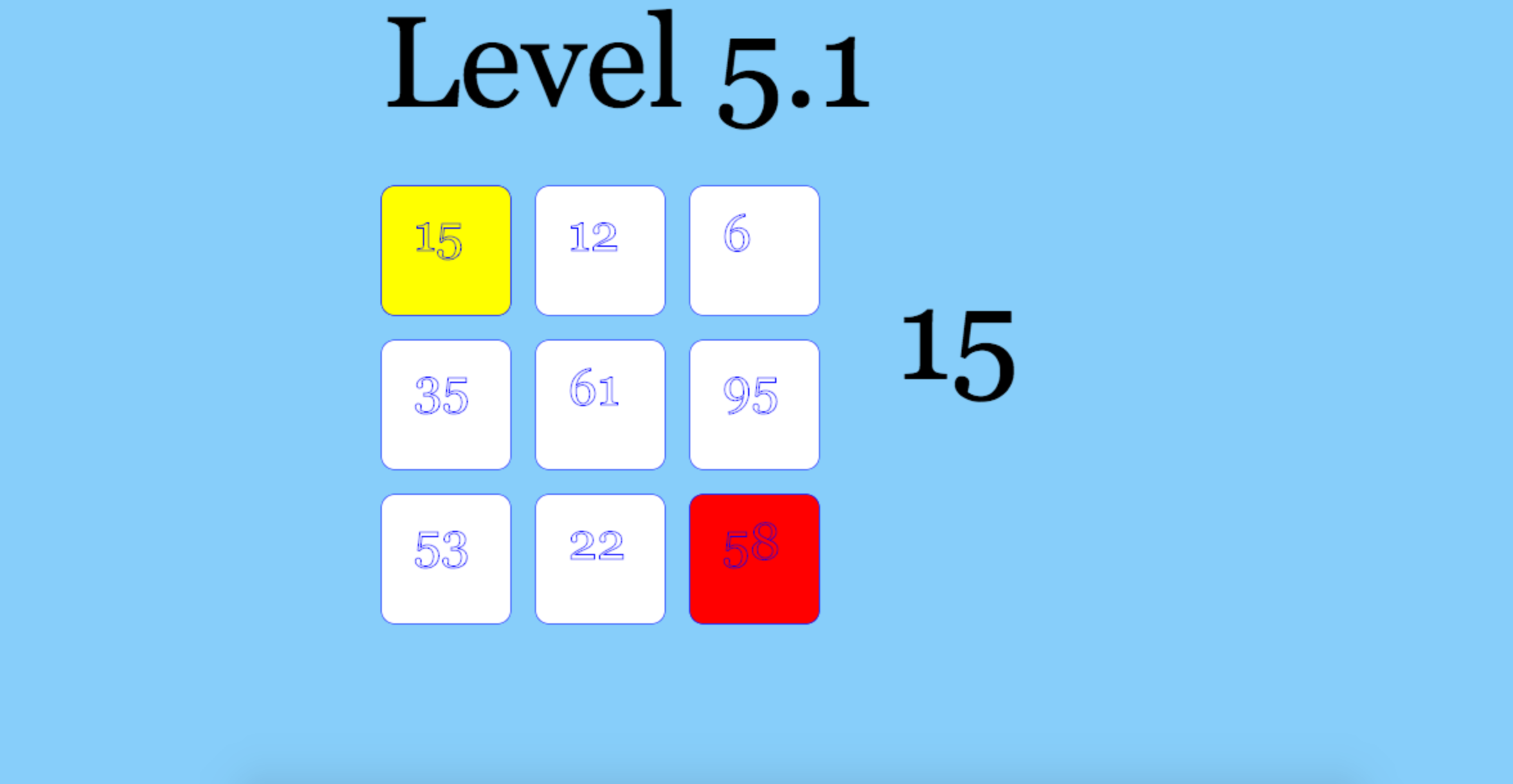
本小关方格规模为3*3,左上角黄色格子为起点,右下角红色格子为重点,页面右侧有一数字,表示当前所累加的数字之和。通过几次尝试之后,可以发现,从左上角开始,我们可以按下方向键或者右方向键来移动方格,直到到达右下角终点格子,路径所累加的数字和若最大,则视为成功过关,否则失败重新来过。
level_5.2
关卡链接:level_5.2
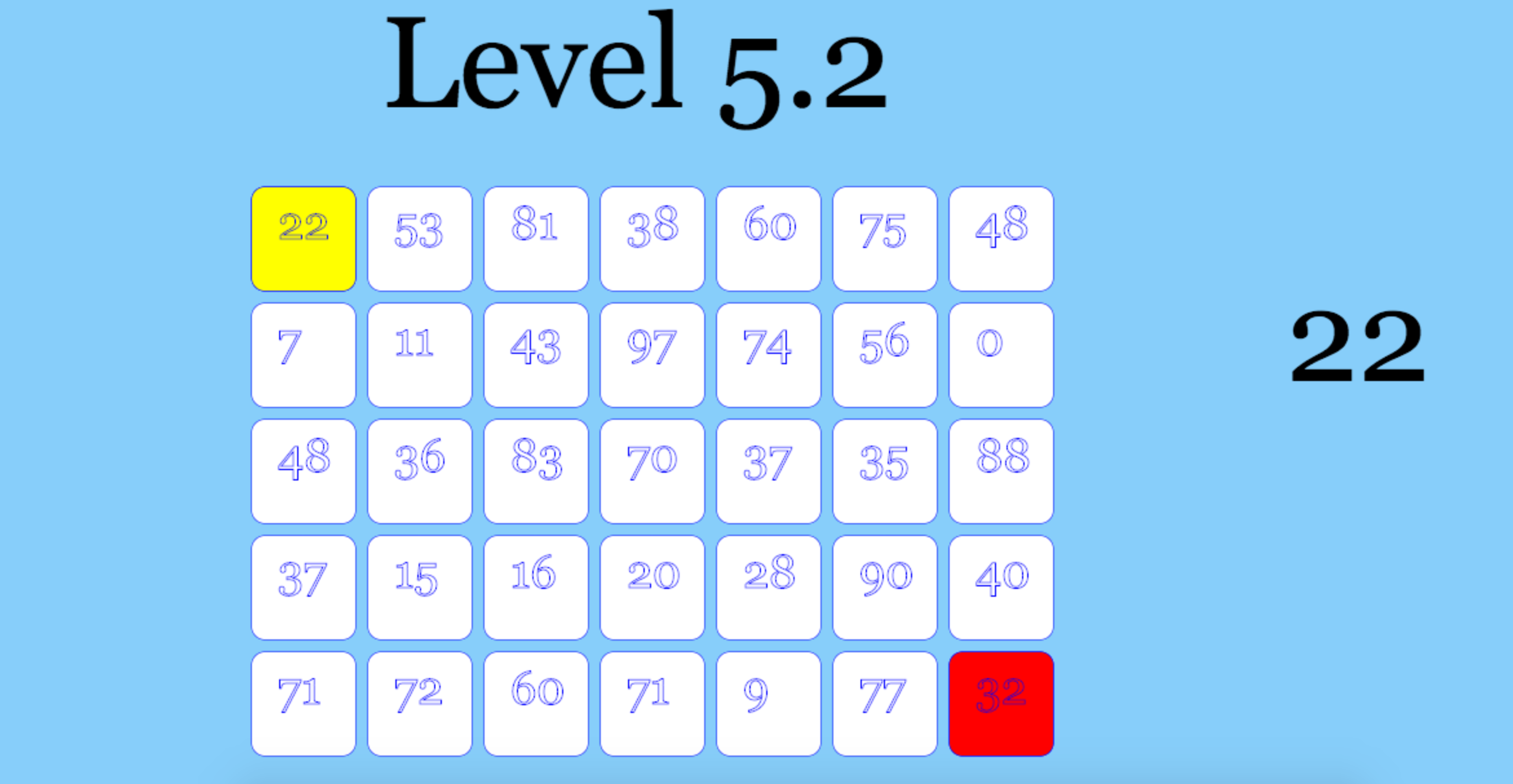
上一小关是3*3,总共只有 C(2, 4)=6 种可能(因为需要向下移动2步,向右移动2步,一共4步,所以是C(2, 4)),我们很容易可以心算出正确的路径,但本关的规模是5*7,可能的路径数有C(4, 10)=210种,没有上一关那么容易了。
我们发现我们尝试的过程中,总会以当前位置附近的格子作为我们决定向右或者向下移动的选择依据,这实际上是一种贪心的思想。但是,贪心有它的局部最优性,即,对于我们所参照的目标(当前位置附近的格子),我们的选择是最优的,但对于从起点到终点即全部方格而言,它并不一定是最优的。
举个简单的例子,你可能会因为当前位置右边是30,下边是100,而选择向下移动,但如果30的右侧有很多100呢,你会因为之前的一次贪心,而错失了后面更好的选择。
因为本小关规模也依旧不大,直接贪心思想尝试,成功的概率也是很大的,但有想法的同学应该可以意识到这种方法的错误的地方,从而进行思考,想到正确的解法。
这就是设立本小关的目的。
level_5.3
关卡链接:level_5.3
本小关才是真正的重头戏了,我们将规模设置为了12*20,可能的方案数为C(11, 30)=54627300,它也依旧不算大(其实还想更大的,只是因为屏幕有限),所以我们将每个数字的范围由之前的0~100改为了280~320,这样,大家心算直接贪心成功的几率就变得很小很小了。
仔细想想,不难发现,对于每个格子而言,能到达它只有两种可能,就是上面和左边。
还是举个例子吧。
就拿3*3,来说,再大规模也是同理的。
15 12 6
35 61 95
53 22 58
我们要求从15到58的最大和路径。
那么对于58而言,它的上一步要么是22,要么是95,那么最大的路径肯定是15到22与95两者较大的那条。
那么如果我们得到下面两个图的结果,就可以得出我们想要的答案。
15 12 15 12 6
35 61 35 61 95
53 22
同理,他们两者依旧可以分解,直至1*1。
这样我们能够提取出一个公式,令a[i][j]表示第i行第j列方格的数值,令dp[i][j]表示从起点到第i行第j列位置所能获得的最大数值和。
则 dp[i][j] = max(dp[i-1][j], dp[i][j-1]) + a[i][j];
递推式已得出,代码就很好写了。
#include <cstring>
#include <cstdio>
#include <iostream>
using namespace std;
const int N = 25;
int dp[N][N];
int a[N][N];
char str[10000];
int main()
{
printf("%s", str);
int len = strlen(str);
int row, col;
row = col = 0;
int num = 0;
//将方格数据转化为矩阵
for(int i=0; i<len; i++)
{
if(str[i] >= '0' && str[i] <= '9')
{
num = num * 10 + str[i] - '0';
}
else if(i > 0 && str[i-1] >= '0' && str[i-1] <= '9')
{
if(str[i] == ']')
{
a[row][col] = num;
num = 0;
if(str[i+1] != ']')
{
col++;
row = 0;
}
}
else if(str[i] == ',')
{
a[row][col] = num;
row++;
num = 0;
}
}
}
//动态规划,按照转移方程,进行迭代
for(int i = 1; i <= row; i++)
for(int j = 1; j <= col; j++)
dp[i][j] = max(dp[i-1][j], dp[i][j-1])+a[i][j];
printf("ans = %d \n", dp[row][col]);
//逆推回来,得到路径
int i = row;
int j = col;
int k = 0;
while(i >=1 && j >= 1)
{
if(dp[i][j] == dp[i-1][j] + a[i][j])
{
str[k++] = 'D';
i--;
continue;
}
if(dp[i][j] == dp[i][j-1]+a[i][j])
{
str[k++] = 'R';
j--;
continue;
}
}
printf("start : ");
for(int p = k-2; p >= 0; p--)
printf("%c > ", str[p]);
printf("end\n");
return 0;
}level_End
关卡链接:level_End
免试题原本在5.3就应该要结束的,但因为做题的玩家(姑且叫玩家吧),不止大一的小鲜肉,还有高年级的道友们,所以为了让大家玩得更愉快,临时增加了本关。
本关乍一看似乎和5.3没有什么区别,但当你使用5.3的方法去移动时,发现到了右下角并不会结束。如果你仔细尝试,才会发现现在方向键上和方向键左是可以按的了。也就是说,现在我们要从左上角走到右下角再走回左上角,即走一个来回,两次路径的方格值总和最大即通过(重复经过的格子只计算一次)。
首先,我们可以将题意转化为从左上角以两条路径走到右下角,获得经过的方格数值总和。那么,依照我们之前的那种思路,
我们令a[i][j]表示第i行第j列方格的数值,令dp[i][j][k][L]四维数组,表示第一条路径到达(i, j),第二条路径到达(k, L)所经过的方格数值总和最大值。那么显然,对于(i, j)来说,有两种可能即(i-1, j), (i, j-1),同理(k, L)有两种可能(k-1, L)和(k, L-1),那么对于(i, j, k, L)就有4种可能性。
用转移方程描述就是
dp[i][j][k][L] = max(
dp[i-1][j][k-1][L],
dp[i-1][j][k][L-1],
dp[i][j-1][k-1][L],
dp[i][j-1][k][L-1]
) + (i != k || j != L) ? a[i][j]+a[k][L] : a[i][j];
讲到这里,我们来看代码吧。
#include <iostream>
#include <cstring>
#include <math.h>
#include <cstdio>
using namespace std;
const int N = 25;
int dp[N][N][N][N];
int a[N][N];
int fa[2][N*N] = {};
char ans[2][100];
char str[10000];
int main()
{
cin>>str;
int len = strlen(str);
int row, col;
row = col = 0;
int num = 0;
//将方格数据转化为矩阵
for(int i=0; i<len; i++)
{
if(str[i] >= '0' && str[i] <= '9')
{
num = num * 10 + str[i] - '0';
}
else if(i > 0 && str[i-1] >= '0' && str[i-1] <= '9')
{
if(str[i] == ']')
{
a[row][col] = num;
num = 0;
if(str[i+1] != ']')
{
col++;
row = 0;
}
}
else if(str[i] == ',')
{
a[row][col] = num;
row++;
num = 0;
}
}
}
int n = col;
//动态规划
for(int i=1; i<=row; i++)
for(int j=1; j<=col; j++)
for(int k=1; k<=row; k++)
for(int l=1; l<=col; l++)
{
int mx = 0;
if(mx < dp[i-1][j][k-1][l])
{
mx = dp[i-1][j][k-1][l];
}
if(mx < dp[i-1][j][k][l-1])
{
mx = dp[i-1][j][k][l-1];
}
if(mx < dp[i][j-1][k-1][l])
{
mx = dp[i][j-1][k-1][l];
}
if(mx < dp[i][j-1][k][l-1])
{
mx = dp[i][j-1][k][l-1];
}
if(i == k && j == l)
dp[i][j][k][l] = mx + a[i][j];
else
dp[i][j][k][l] = mx + a[i][j] + a[k][l];
}
cout<<"the ans = "<<dp[row][col][row][col]<<endl;
//逆推得到路径
int cnt = 0;
int i=row, j=col, k=row, l=col;
while(1)
{
if(i == 1 && j == 1 && k == 1 && l == 1)
break;
dp[i][j][k][l] -= a[i][j];
if(i != k || j != l)
dp[i][j][k][l] -= a[k][l];
if(dp[i][j][k][l] == dp[i-1][j][k-1][l])
{
ans[0][cnt] = 'U';
ans[1][cnt] = 'D';
cnt++;
i--;k--;
}
else if(dp[i][j][k][l] == dp[i-1][j][k][l-1])
{
ans[0][cnt] = 'U';
ans[1][cnt] = 'R';
cnt++;
i--;l--;
}
else if(dp[i][j][k][l] == dp[i][j-1][k-1][l])
{
ans[0][cnt] = 'L';
ans[1][cnt] = 'D';
cnt++;
j--;k--;
}
else
{
ans[0][cnt] = 'L';
ans[1][cnt] = 'R';
cnt++;
j--;l--;
}
}
//输出路径
cout<<"load_one > ";
for(int i=0; i<cnt; i++)
cout<<ans[0][i]<<" > ";
cout<<"end"<<endl;
cout<<"load_two > ";
for(int i=cnt-1; i>=0; i--)
cout<<ans[1][i]<<" > ";
cout<<"end"<<endl;
return 0;
}