GroupBlog

题意

题目描述 Description

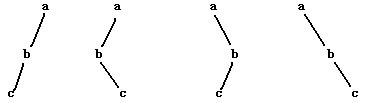
我们都很熟悉二叉树的前序、中序、后序遍历，在数据结构中常提出这样的问题：已知一棵二叉树的前序和中序遍历，求它的后序遍历，相应的，已知一棵二叉树的后序遍历和中序遍历序列你也能求出它的前序遍历。然而给定一棵二叉树的前序和后序，你却不能确定其中序遍历序列，考虑如下图中的几棵二叉树：

所有这些二叉树都有着相同的前序遍历和后序遍历，但中序遍历却不相同。

输入描述 Input Description

输入文件共2行，第一行表示该树的前序遍历结果，第二行表示该树的后序遍历结果。输入的字符集合为{a-z}，长度不超过26。

输出描述 Output Description

输出文件只包含一个不超过长整型的整数，表示可能的中序遍历序列的总数。

思路

显然，中序遍历的数量一定和只有一个子节点的节点数目有关。
比如a的唯一子节点是b，那么先序遍历中一定是ab，后序遍历中一定是ba，即相邻且位置相反。
随便画一个二叉树观察即可明白。
那么，得出的节点数目为n，答案就是2^n。

代码

#include <iostream>
#include <cstring>
#include <math.h>
#include <cstdio>
#include <stack>

using namespace std;

const int N = 30;
char a[N], b[N];

int main()
{
    cin>>a>>b;
    int ans = 1;
    int len = strlen(a);
    for(int i=1; i<len; i++)
    {
        for(int j=1; j<len; j++)
        {
            if(a[i-1] == b[j] && a[i] == b[j-1])
                ans <<= 1;
        }
    }
    cout<<ans<<endl;
    return 0;
}