GroupBlog

1. 什么是Trie树

Trie树，也叫字典树，是一种树形结构，常用于统计、排序和保存大量字符串，利用字符串的公共前缀来减少查询时间，以空间换取时间。

2. 基本结构

Trie树不同于我们常接触到的二叉树，而是N叉树，例如，如果我们要将许多单词（小写）用Trie树来进行保存，那么此时的Trie树为26叉树，因为总共有26个小写字母。
例如：
我们要储存inn int ate age adv ant 这五个单词，那么所构成的Trie树为下图所示。

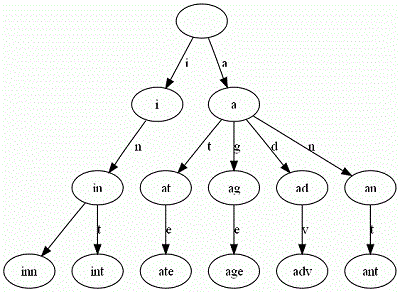
在Trie树中，每个字符串都被分为单个字符按照顺序逐层标记于树上。
需要说明三点：
<1>根节点只保存子节点地址，不保存数据
<2>每个节点中并不保存当前前缀的字符串，而是在逻辑上，以从根节点到当前节点的路径来表示。
<3>每个节点中都保存一int值，表示树中所有字符串以当前路径为前缀的字符串的数量。
树节点结构体定义如下：

typedef struct Node
{
    int num；               //保存当前路径为前缀的字符串的总数
    struct Node *next[MAX]; //保存子节点的地址。
}

3. 基本操作

<1> 添加
从根节点开使，获取需要添加的字符串的第一个字符，根据字符值获取next[]数组中相应子树的地址，并进行跳转。如果子树地址为空则需先新建节点，初始化num=1，并将新建节点的next数组全部置为空。然后跳转。若不为空，将num++；
从当前节点开始，对字符串的第二个字符进行上述操作。
…
字符串遍历完，此时添加成功
<2> 查找
对需检索的字符串进行类似上述操作，不同的是若在字符串遍历完毕之前，子树地址为空，表示该字符串并不在此树中。
<3> 删除
一般很少使用，过程细节类似于添加操作。不同处为对num进行减操作。

4. 性能

Trie主要用于查找。
在Trie树中查找一个关键字的时间和树中包含的结点数无关，而取决于组成关键字的字符数。而二叉查找树的查找时间和树中的结点数有关O(log2n)。
如果要查找的关键字可以分解成字符序列且不是很长，利用Trie树查找速度优于二叉查找树。

5. 应用例题

hihocoder 1014 Trie树
题目大意：
给定词典，对于每个输入的关键字，输出词典中以该关键字为前缀的字符串总数。
输入
输入的第一行为一个正整数n，表示词典的大小，其后n行，每一行一个单词（不保证是英文单词，也有可能是火星文单词哦），单词由不超过10个的小写英文字母组成，可能存在相同的单词，此时应将其视作不同的单词。接下来的一行为一个正整数m，表示小Hi询问的次数，其后m行，每一行一个字符串，该字符串由不超过10个的小写英文字母组成，表示小Hi的一个询问。

在20%的数据中n, m<=10，词典的字母表大小<=2.

在60%的数据中n, m<=1000，词典的字母表大小<=5.

在100%的数据中n, m<=100000，词典的字母表大小<=26.

输出
对于小Hi的每一个询问，输出一个整数Ans,表示词典中以小Hi给出的字符串为前缀的单词的个数。

6. 代码

#include<iostream>
#include<algorithm>
#include<stdio.h>
#include<string.h>
#include<stdlib.h>

using namespace std;

typedef struct Node
{
    int num;
    struct Node *next[26];
}tree;


void init(tree *t)
{
    for(int i=0;i<26;i++)
    {
        t->next[i] = NULL;
    }
}

void add(tree *t,char s[])
{
    int len = strlen(s);
    for(int k=0; k<len; k++)
    {
        if(t->next[s[k]-'a'] == NULL)
        {
            tree *z = (tree*)malloc(sizeof(tree));
            init(z);
            z->num = 1;
            t->next[s[k]-'a'] = z;
        }
        else
        {
            t->next[s[k]-'a']->num++;
        }
        t=t->next[s[k]-'a'];
    }
}

int find(tree *t, char str[])
{
    int len = strlen(str);
    for(int i=0;i<len;i++)
    {
        if(t->next[str[i]-'a'] == NULL)
            return 0;
        else
        {
            t = t->next[str[i]-'a'];
        }
    }
    return t->num;
}

int main()
{
    int n;
    scanf("%d",&n);
    char str[10];
    tree *root = (tree*)malloc(sizeof(tree));
    init(root);
    while(n--)
    {
        scanf("%s",str);
        add(root, str);
    }
    scanf("%d",&n);
    while(n--)
    {
        scanf("%s",str);
        printf("%d\n",find(root, str));
    }
    return 0;
}