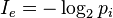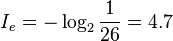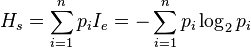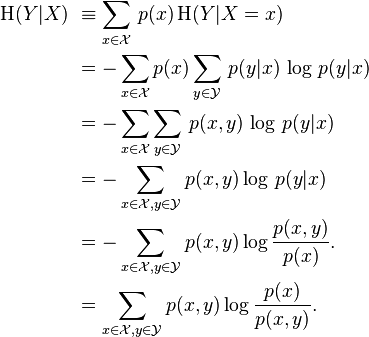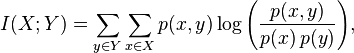信息有大小吗,如何度量信息的大小?如何度量信息之间的关系?
今天主要讨论的几个问题,它是 信息论 的基础,相信看完这篇文章你会感觉:
其实每门学科都有它的神奇之处:)
信息熵
在日常生活中,我们应该遇到过这样类似的情况:有的人简单说了一句话,我们感觉这句话信息量好大,一时缓不过神来。有的人说了一堆话,感觉和没说一样,半天提取不出来重点信息。
如果遇到过这种情况,我们应该有所感觉——信息应该是可以度量的。
确实,信息的确可以度量。
被喻为信息论之父——克劳德·香农,在 1948 年它的著名论文“通信的数学原理”(A Mathematic Theory if Communication)中提出了“ 信息熵 ”的概念,从而解决了信息的度量问题。
我们从一个例子引入信息熵,信息是一个很抽象的东西,我和小美在聊天,小美说:明天天气真好,是晴天,气温有25度。这句话很短,对于我来说,我要从这句话中提取出有用的信息,但问题来了,我不可能在听到小美说的话后就立刻在自己的脑袋里刻上这条信息。明天天气是否真的那么好?会是晴天吗?如果是晴天,可能达到25度吗?也就是说这条信息具有 不确定性,不确定性和信息的大小是密切相关的,如果一条信息的不确定性很大,我们要获取到它,必须查阅很多的资料。明天是晴天?我先去看看天气预报。如果小美说今天天气真好,是晴天。这句话的不确定性就非常小,因为我知道今天是什么天气。
从上面的例子我们知道:信息的信息量与其不确定性有着直接的关系。
不确定性就是事件的概率和事件的结果。明天是不是晴天,简单分类事件的结果会有两种,晴天或不是晴天,晴天的概率是 50%,不是晴天的概率是 50% 。
信息熵 就是用来衡量信息量的大小。熵这个字出自与热力学,表示系统混乱的程度,在信息论中我们用信息熵来表示信息的大小。简单理解信息的不确定性越大,信息熵就越大,信息的不确定性越小,信息熵也就越小。
在说信息熵之前还要引入一个概念:自信息量
自信息量 是用来描述某一条信息(自己)的大小。
公式如下:
先举个简单的例子,比如英文中的 26 个字母,假设每个字母出现的概率是相等的。那么其中一个字母的自信息量大小就是
这个公式以 2 为底数,单位为bit,含义是用多少为二进制数能衡量该信息的大小。
我们也可以用其他进制来作为底数,仅仅是单位不同。
通常我们衡量的都是一个系统的信息量,系统 S 内存在多个事件S = {E1,…,En},每个事件的概率分布P = {p1, …, pn},熵是整个系统的 平均消息量
说了这么多 信息熵 很大的话是时候来看看如何度量信息的大小:)
公式如下:
从公式我们能看出 熵是接收的每条消息中包含的信息的平均量,也被称为平均自信息量。
这个公式怎么理解呢,比如我们要衡量一篇英语文章的信息熵,对于任意一篇文章来说,每个字母出现的频率是不同的,所以
H = -(P1*logP1 + P2*logP2 + … + P26*logP26)
Pi 表示每个英文字母出现的概率,英语的平均信息熵是 4.03 比特,而中文的信息熵高达 9.65 比特。所以说中文博大精深^_^。
这也就是为什么很厚的一本英文书翻译成中文后变薄了很多。
条件熵
从上面我们知道了信息熵是用来衡量信息的不确定程度。信息熵越大,说明信息的不确定程度越大,信息熵越小,说明信息的不确定程度越小。
然而,在实际当中,我们常常希望信息熵越小越好,这样我们就能 少费点力气 来确定信息。
举个最简单的栗子:机器翻译,将英语文章翻译为汉语时,最令人头疼的就是 一词多义问题 。比如 Bush 一词是美国总统布什的名字,但它同时也具有灌木丛的意思。在机器翻译中,机器如何判断将 Bush 一词翻译成布什总统还是灌木丛?此刻信息的不确定性较大,就说明信息熵较大。
那么如何减小信息熵呢,最简单的方法就是增加上下文。前面提到的只是一元模型,为降低信息的不确定性也就是减小信息熵的大小,我们引入二元模型或更高阶的模型。
来看看 二元模型——条件熵,条件熵表示在已知第二个随机变量 X 下第一个随机变量 Y 信息熵的大小。条件上用 H(Y|X) 表示。
在随机变量 X 的基础上我们引入随机变量 Y,假设 Y 和 X 有一定的关系。那么 Y 的信息熵会相对减小。
还是刚才的例子,机器不知道将 Bush 翻译成灌木丛还是总统布什,如果我们先引入 美国,总统 等这类单词作为信息的上下文,如果这些出现,就将 Bush 翻译为总统布什,那么翻译正确的概率就大多了,也就是说信息的不确定性在减小,信息熵也就随之减小。类比,如果是搜索引擎呢,我们搜索 计算机技术 这个关键字出来的结果很多很多,我们也不知道哪个是自己想要的,因为信息的不确定性太大了。那么如果搜索引擎提供给用户上下文让用户进行选择,消除一些不确定性。比如计算机技术中的 编程语言,数据库,操作系统 等相关搜索,那么用户会更容易得到自己想要的搜索结果,用户体验会更好(当然现在的搜索引擎就是这么做的)。这也就是 条件熵 起的作用。
然而只有当随机变量 X 和随机变量 Y 有关系时才能减小不确定性。机器翻译中我们加入 食物 关键字能减小 Bush 翻译的不确定性吗?当然不能。
那么如何衡量两个信息的相关程度,我们引入 互信息。
互信息
来看下维基百科的定义
在概率论和信息论中,两个随机变量的互信息(Mutual Information,简称MI)或转移信息(transinformation)是变量间相互依赖性的量度。
定义中说明了互信息是变量间 相互依赖的亮度,简单来说就是相关程度。互信息我们用如下来表示:
在机器翻译 Bush 这个例子中,我们引入 上下文 来消除不确定性,那么上下文该如何引入呢,在了解互信息后,应该知道,只用引入和 Bush 翻译成总统布什互信息大的一些词即可。比如美国,国会,总统等等。再引入一些和灌木丛互信息大的词如森林,树木等等。在翻译 Bush 时,看看上下文哪类词多就好。
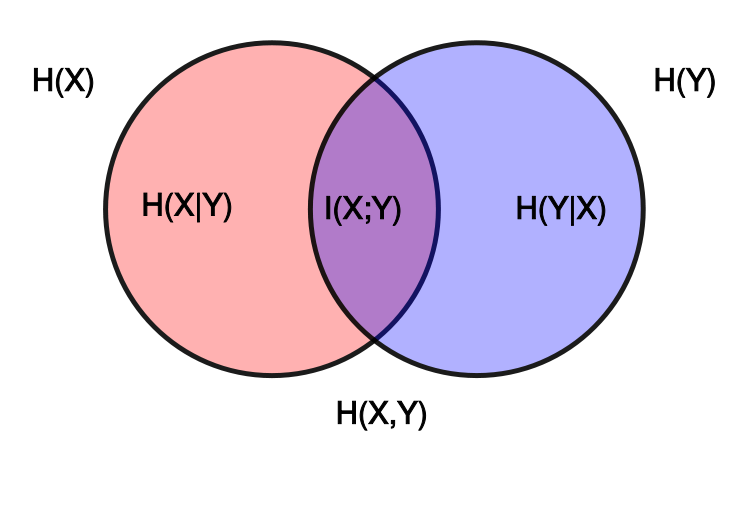
最后用一张图来表示 信息熵,条件熵,互信息 之间的关系。
完
参考资料: