前一阵看的数据结构比较多,刚好放假没事,把一些我认为重要的写成博客记录下来。
今天主要看的是树中的两个比较重要的数据结构
前缀树和后缀树
这两个树的应用特别广,但是我认为常看课外技术书籍的,博客的都知道,但是一些专注于课本的同学可能就没听说过了。比如我们的课本 - -。
开始吧 ^_^
先说下前缀后缀的概念吧。
比如单词apple。app和appl是单词的前缀,ple和pple是单词的后缀,前缀必须从开头字符起,结尾不定,后缀必须以末尾字符结尾,起点不限制。
一.前缀树
简述:又名单词查找树,tries树,一种多路树形结构,常用来操作字符串(但不限于字符串),和hash效率有一拼(二者效率高低是相对的,后面比较)。
性质:不同字符串的相同前缀只保存一份。
操作:查找,插入,删除。
举个例子:
假设有这么几个单词
(1)
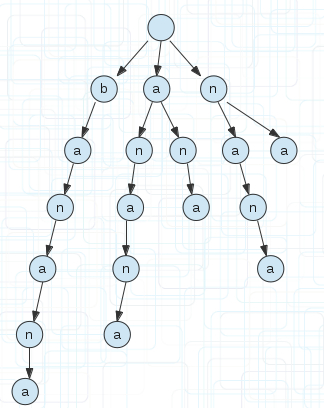
把它存入一棵前缀树后
(2)
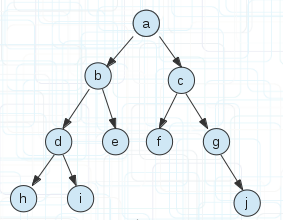
给出的单词都是a字母开头的,所以存储时他们可以共用开头字母a,接下来b字母有3个,所以它们可以共用一个字母b。
也就是说相同的前缀每个字母可以共用一个空间,我有1000个a开头的字母,那么它们也只需要一个空间a即可。
比如上图abdh和abdi这两个,也只有h和i不用而已。
从(1)(2)图片我们可以看出前缀树相对来说是非常节省空间的,比如上面两个图片,(1)用数组存储18个空间,(2)只用了10个空间。(数据量大会忽略指针域所占空间的)。
除了节省空间外它的查找效率也是非常高的,只需要O(logL), L是单词的长度。一般来说我们的单词长度都不会太长吧,就那常见的来说也就20or30?
1.查找操作:
上面的图片只是简单的例子,如果我们用数组来实现的话,树根应该是一个空节点,它有指针域指向单词的所有开头字母也就是a-z。
按照字符串的每个字符来比较,比如abdi,a符合,然后比较第二个字母是b,继续比较直到末尾...
查找操作还是很简单的。
有个疑问就是上面图片中有abdh这个单词,我们怎么知道有没有abd或者ab这个单词呢,毕竟它也在这棵前缀树中。
简单,我们只需要给每个节点增加一个引用计数即可,比如有1000个a开头的字母,那么a的应用计数就是1000,ab开头的有999个,那么b的引用计数就是999,
可见b的引用计数小于a,所以存在单词a,那么得出结论:
某个字符串在前缀树中的结尾字母的引用计数如果大于末节点的下一个节点的引用计数(大1),说明存在此单词。
2.插入操作:
依次比较经过的每一个字母,如果字母存在,则给字母的引用计数加1,如果该字母不存在,直接从该字母开始到此字符串的末尾的每一个字母
连接到这棵前缀树上。
3.删除操作:
依次比较经过的每一个字母,给所经过的每个字母的引用计数值减1,如果该引用计数值为0的话,则删除此节点,此节点往后的节点也删除,
因为必定都属于这个单词。
4.重点:前缀树的应用
前缀树还是很好理解,但是它的应用是非常广的。
<1.字符串的快速检索
前面也说了字典树的查询时间复杂度是O(logL),L是字符串的长度。所以效率还是比较高的。
前面说了字典树的效率和hash表有一拼,这里来分析下,网上的一部分文章说的都是字典树的效率比hash表高。我觉得还是相对来看比较好,各有个的特点吧。
hash表,通过hash函数把所有的单词分别hash成key值,查询的时候直接通过hash函数即可,都知道hash表的效率是非常高的为O(1),直接说字典树的查询效
率比hash高,难道有比O(1)还快的- -。
hash:
当然对于单词查询,如果我们hash函数选取的好,计算量少,且冲突少,那单词查询速度肯定是非常快的。那如果hash函数的计算量相对大呢,且冲突律高呢?
这些都是要考虑的因素。且hash表不支持动态查询,什么叫动态查询,当我们要查询单词apple时,hash表必须等待用户把单词apple输入完毕才能hash查询。
当你输入到appl时肯定不可能hash吧。
字典树(tries树):
对于单词查询这种,还是用字典树比较好,但也是有前提的,空间大小允许,字典树的空间相比较hash还是比较浪费的,毕竟hash可以用bit数组。
那么在空间要求不那么严格的情况下,字典树的效率不一定比hash若,它支持动态查询,比如apple,当用户输入到appl时,字典树此刻的查询位置可以就到达l这个
位置,那么我在输入e时光查询e就可以了(更何况如果我们直接用字母的ASCII作下标肯定会更快)!字典树它并不用等待你完全输入完毕后才查询。
所以效率来讲我认为是相对的。
<2.字符串排序
从上图(2)我们很容易看出单词是排序的,先遍历字母序在前面的比如abdh,然后abdi。
减少了没必要的strcmp
这个很好理解。
<3.最长公共前缀
abdh和abdi的最长公共前缀是abd,遍历字典树到字母d时,此时这些单词的公共前缀是abd。
<4.自动匹配前缀显示后缀
我们使用辞典或者是搜索引擎的时候,输入appl,后面会自动显示一堆前缀是appl的东东吧。
那么有可能是通过字典树实现的,前面也说了字典树可以找到公共前缀,我们只需要把剩余的后缀遍历显示出来即可。^_^
二.后缀树
简介:后缀树,就是把一串字符的所有后缀保存并且压缩的字典树。相对于字典树来说,后缀树并不是针对大量字符串的,而是针对一个或几个字符串来解决问题,
比如字符串的回文子串,两个字符串的最长公共子串等等,后面应用会说。
性质:一个字符串构造了一棵树,树中保存了该字符串所有的后缀。
操作:就是建立和应用。
1.建立后缀树
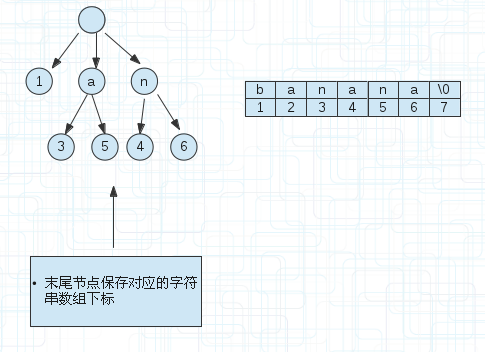
比如单词banana,它的所有后缀显示到下面的。1代表从第一个字符为起点,终点不用说都是字符串的末尾。
以上面的后缀,我们建立一颗后缀树。如下图,为了方便看到后缀,我没有合并相同的前缀
(3)
前面简介的时候我们说了,后缀树是把一个字符串所有后缀压缩并保存的字典树。
压缩一会再说,简介里面说了是字典树,所以我们把字符串的所有后缀还是按照字典树的规则建立,就成了上图(3)的样子。
注意还是和字典树一样,根节点必须为空。
下面说下更加节省空间的方案,也就是上面提到的压缩。
(4)
因为有些后缀串可能是单串,并不和其他的共用同一个前缀。
比如图(4)的banana这个后缀串,直接可以用1来表示起点,终点是默认的。
图(4)的a节点后面有两个节点标记3和5是右边字符数组的下标,对应着a->3-7,a->5-7。因为a是共有的前缀。
2.重点说下后缀树的应用,它能解决大多数字符串的问题
<1.查找某个字符串s1是否在另外一个字符串s2中
这个很简单,如果s1在字符串s2中,那么s1必定是s2中某个后缀串的前缀。
理解以下后缀串的前缀这个词,其实每个后缀串也就是起始地点不同而已,前缀也就是从开头开始结尾不定。
后缀串的前缀就可以组合成该原先字符串的任意子串了。
比如banana,anan是anana这个后缀串的前缀。
<2.指定字符串s1在字符串s2中重复的次数
看图(3),比如说banana是s1,an是s2,那么计算an出现的次数实际上就是看an是几个后缀串的前缀。
上图的a节点是保存所有起始为a字母的后缀串,我们看a字母后的n字母的引用计数即可。
先说下广义后缀树,前面说了后缀树可以存储一个或多个字符串,当存储的字符串数量大于等于2时就叫做广义后缀树。
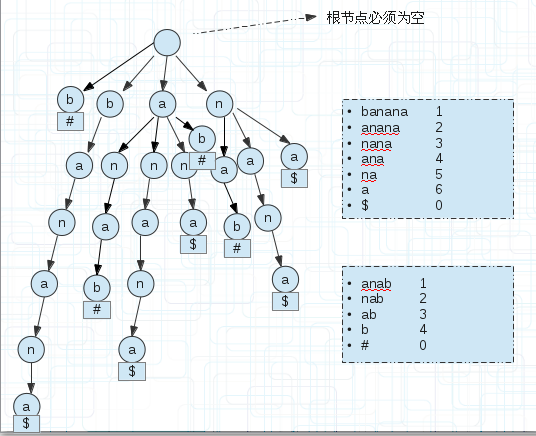
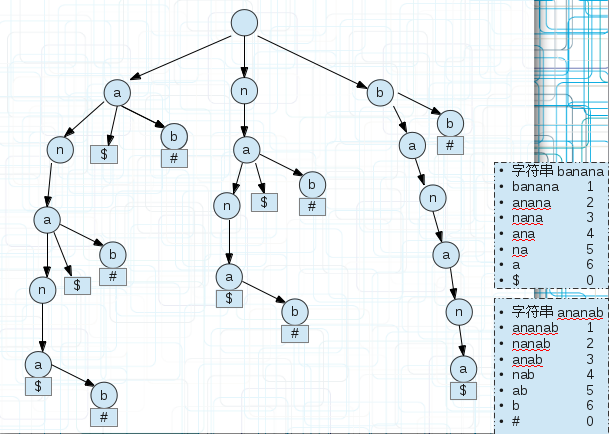
<3.两个字符串S1,S2的最长公共部分(广义后缀树)建立一棵广义后缀树,如下图(5)
(5)
$和#是为了区分字符串的。
我们为每个后缀串末尾单独添加一个空间存储区分字符串的符号。
那么怎么找s1和s2串最长的公共部分?
遍历每个后缀串,如果其引用计数为1则直接跳过,因为不可能有两个子串存放在这里,当引用计数>1时,往下遍历,直到分叉分别记录子串的符号,
如果不同,说明他们是不同字符串的,记录已经匹配的值即可,若相同继续下一次遍历。
上图的ana部分,到ana时,子串$结束,然后继续向下,子串anab以#结束,那么匹配了ana。
<4.最长回文串(广义后缀树)
把要求的最长回文串的字符串s1和它的反向(逆)字符串s2建立一棵广义后缀树。
回文串有一个定义就是正反相同,也就是正着和反着可以重和在一起,那么我们直接看这棵广义后缀树的共同前缀即可,每个banana的子串和ananab的子串重合的部分
都是回文串,我们只需要找到最长的即可。比如上面的anana,从后面不同的标记可以看出两个字符串的某个后缀都有这个前缀,能完美重合到一起。即它是回文串。
记录Max,每次找到一个回文串比较即可。