昨天突然有人问我AVL树,我以前以为自己还会,结果给人家讲着讲着就没有说清楚。今天就自己把AVL写了一遍总结一下,如果有写的不对地方欢迎大家拍砖。。。
AVL定义:
(1)左子树和右子树的深度之差的绝对值小于等于1;
(2)左子树和右子树也是平衡二叉树;
下面的描述中需要用到平衡因子:节点的左子树深度与右子树深度之差。
要建立一颗平衡二叉树需要经过一下步骤:
(1)查找应插位置,同时记录离插入位置最近的可能失衡的节点A(寻找平衡因子不等于0)
while(p != NULL)
{
if(p->bf != 0)
{
A = p;
FA = fp;
}
fp = p;
if(k < p->key)
p = p->lchild;
if(k < fp->key)
fp->lchild = s;
else
fp->rchild = s;
if(k < A->key)
{
B = A->lchild;
A->bf += 1;
}
else
{
B = A->rchild;
A->bf -= 1;
}
p = B;
while(p != s)
{
if(k < p->key)
{
p->bf = 1;
p = p->lchild;
}
else
{
p->bf = -1;
p = p->rchild;
}
}前面那些东西可能看起来还比较清晰,容易理解我也就不多说什么了。第(5)步比较复杂咱们单独来看~~。首先要知道平衡因子的概念,如果不知道看前面介绍。然后就是把插入过程如果失衡分成4种情况来处理。
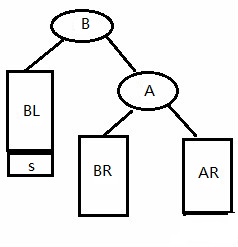
第一种:LL型 旋转后:
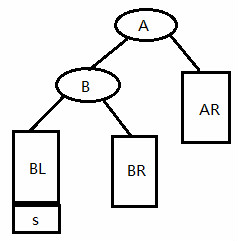
if(A->bf == 2 && B->bf == 1) //LL
{
B = A->lchild;
A->lchild = B->rchild;
B->rchild = A;
A->bf = 0;
if(FA == NULL)
*avlt = B;
else if(FA->lchild == A)
FA->lchild = B;
else
FA->rchild = B;
B->bf = 0;
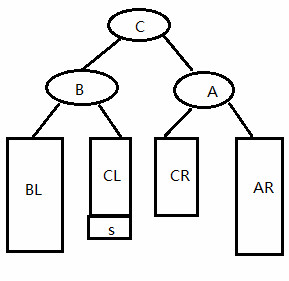
} 第二种:LR型
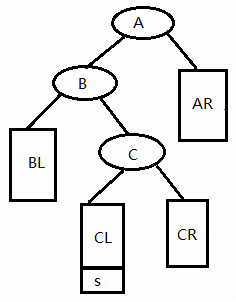
else if(A->bf == 2 && B->bf == -1) //LR
{
B = A->lchild;
C = B->rchild;
B->rchild = C->lchild;
C->lchild = B;
A->lchild = C->rchild;
C->rchild = A;
if(C->key > s->key) //在CL下插入s
{
A->bf = -1;
B->bf = 0;
C->bf = 0;
}
else if(C->key < s->key) //在CR下插入s
{
A->bf = 0;
B->bf = 1;
C->bf = 0;
}
else //C本身就是插入的新节点s
{
A->bf = 0;
B->bf = 0;
}
if(FA == NULL)
*avlt = C;
else if(FA->lchild == A)
FA->lchild = C;
else
FA->rchild = C;
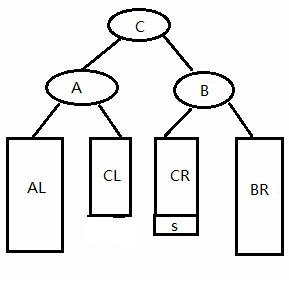
}第三种:RL型
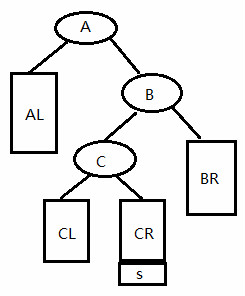
else if(A->bf == -2 && B->bf == 1) //RL
{
B = A->rchild;
C = B->lchild;
A->rchild = C->lchild;
B->lchild = C->rchild;
C->lchild = A;
C->rchild = B;
if(C->key > s->key)
{
A->bf = 0;
B->bf = -1;
C->bf = 0;
}
else if(C->key < s->key)
{
A->bf = 1;
B->bf = 0;
C->bf = 0;
}
else
{
A->bf = 0;
B->bf = 0;
}
if(FA == NULL)
*avlt = C;
else if(FA->lchild == A)
FA->lchild = C;
else
FA->rchild = C;
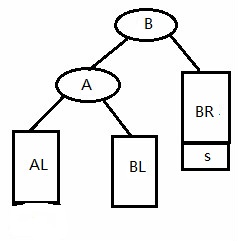
}第四种:RR型
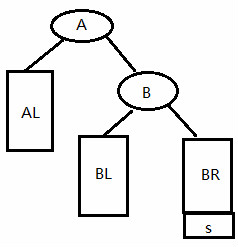
else if(A->bf == -2 && B->bf == -1) //RR
{
B = A->rchild;
A->rchild = B->lchild;
B->lchild = A;
A->bf = 0;
B->bf = 0;
if(FA == NULL)
*avlt = B;
else if(FA->lchild == A)
FA->lchild = B;
else
FA->rchild = B;
}