题目:
Given a string
S
, find the longest palindromic substring in
S
. You may assume that the maximum length of
S
is 1000, and there exists one unique longest palindromic substring.
参考资料:“马拉车”算法的过程解释来自 http://blog.csdn.net/dyx404514/article/details/42061017
大意:
求给定字符串的最长回文子序列(回文是指正序和逆序相等)。
思路:
开始拿到题后没有一丝思路,只好用暴力枚举碰一碰,说不定就AC了呢?结果发现我还是太年轻,意料之中的超时了。经过搜索发现了一种称为“马拉车”的算法,非常巧妙,时间复杂度仅为O(n)。
1、为了将字符串的奇数个和偶数个统一起来使用一个操作,该算法对字符串进行预处理使之都变成奇数个:在字符串的首尾和每个字符中间都插入一个特殊符号。如:ccd预处理后为:#c#c#d#,abba预处理后为:#a#b#b#a
2、在预处理之后寻找以字符串中每个字符为中心时(包括自身)的回文串长度,并记录进辅助数组v中,该辅助数组v的下标对应字符串的每个下标,所以该问题就变成了如何求得辅助数组v中每个元素的值。
3、为了快速求得辅助数组的具体值可以利用已经保存的结果和回文的性质来求,具体步骤如下:
(1)、
首先从左往右依次计算Len[i],当计算Len[i]时,Len[j](0<=j<i)已经计算完毕。设P为之前计算中最长回文子串的右端点的最大值,并且设取得这个最大值的位置为po,分两种情况:
第一种情况:i<=P
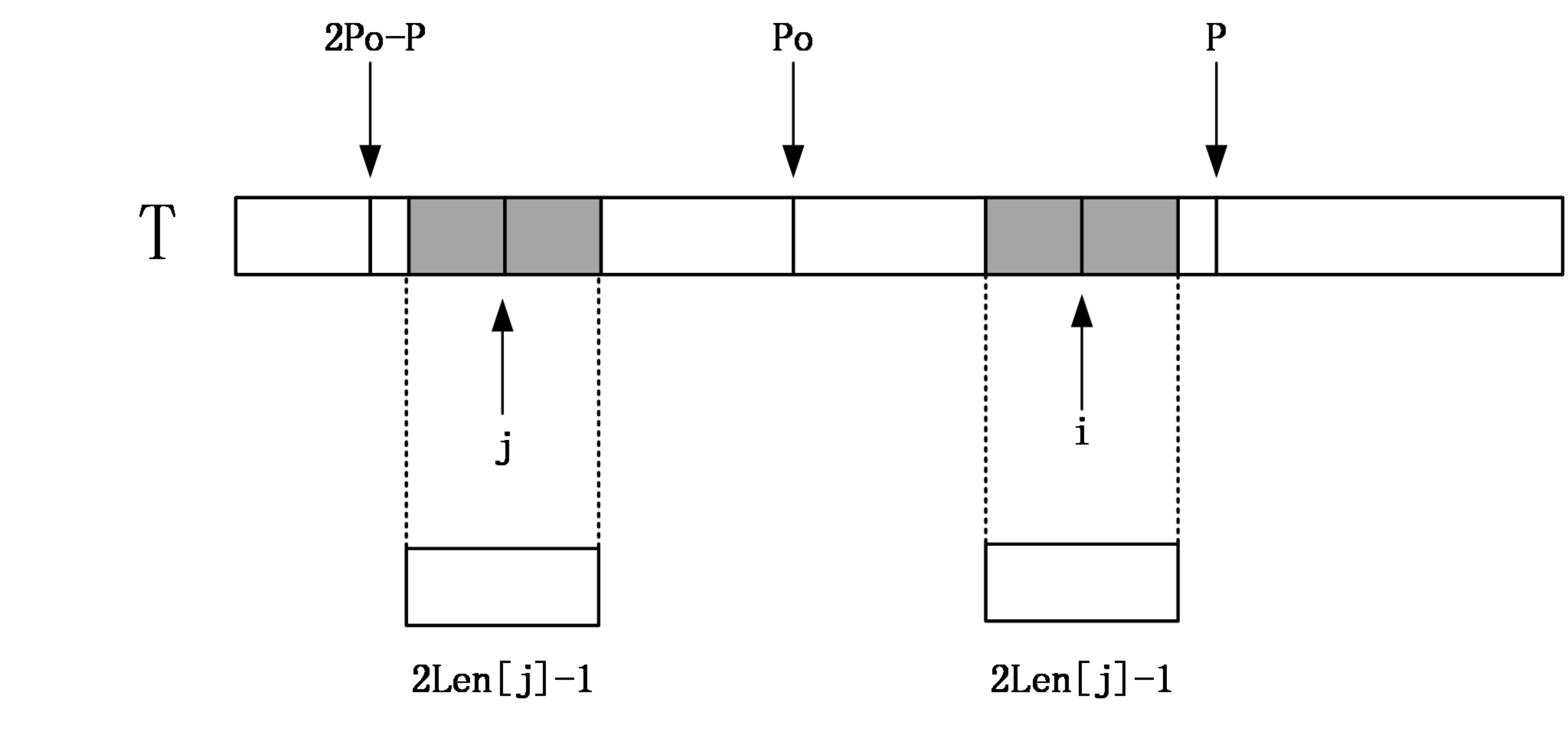
那么找到i相对于po的对称位置,设为j,那么如果Len[j]<P-i,如下图:
那么说明以j为中心的回文串一定在以po为中心的回文串的内部,且j和i关于位置po对称,由回文串的定义可知,一个回文串反过来还是一个回文串,所以以i为中心的回文串的长度至少和以j为中心的回文串一样,即Len[i]>=Len[j]。因为Len[j]<P-i,所以说i+Len[j]<P。由对称性可知Len[i]=Len[j]。
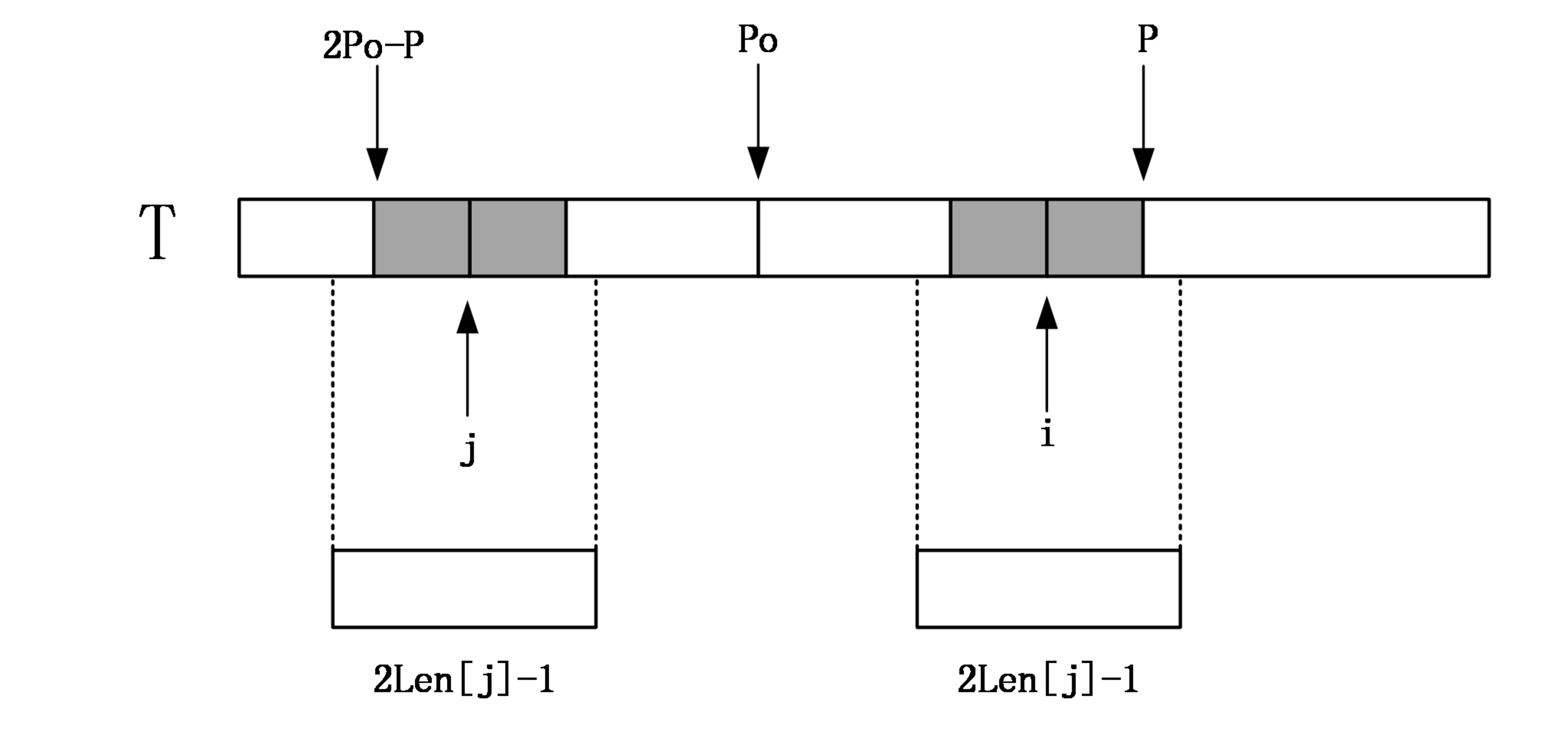
如果Len[j]>=P-i,由对称性,说明以i为中心的回文串可能会延伸到P之外,而大于P的部分我们还没有进行匹配,所以要从P+1位置开始一个一个进行匹配,直到发生失配,从而更新P和对应的po以及Len[i]。
第二种情况: i>P
如果i比P还要大,说明对于中点为i的回文串还一点都没有匹配,这个时候,就只能老老实实地一个一个匹配了,匹配完成后要更新P的位置和对应的po以及Len[i]。
代码:
class Solution {
public :
std::string longestPalindrome(std::string s) {
int maxpos = 0, mid = 0;
std::vector<int> v;
int max = 0;
std::string tmp = s;
init(tmp);
v.resize(tmp.size());
for (int i = 0; i < tmp.size(); ++i) {
//如果可以直接从以前计算过的里边取出值
if (i < maxpos) {
v[i] = v[mid * 2 - i] < (maxpos - i) ? v[mid * 2 - i] : (maxpos - i);
} else { //不能直接从以前计算过的里边取值
v[i] = 1;
}
//向两遍扩展,寻找以i为中心最长的
while(i - v[i] >= 0 && i + v[i] < tmp.size() && tmp[i - v[i]] == tmp[i + v[i]]) {
++v[i];
}
//记录v中最大值的下标,便于函数的最后返回子串
if (v[i] >= v[max]) {
max = i;
}
//更新最大位置和中间位置
if (v[i] + i > maxpos) {
maxpos = v[i] + i;
mid = i;
}
}
int i, j;
//如果max为奇数则表示前边加了v[max]/2+1个#
if (max % 2) {
i = max / 2 - v[max] / 2 + 1;
} else { //max为偶数则表示加了v[max]/2个#
i = max / 2 - v[max] / 2;
}
//v中存储的是预处理后的字符串,减一后表示原字符串的最大回文
j = v[max] - 1;
return s.substr(i,j);
}
private:
void init(std::string &s)
{
s.resize(s.size() * 2 + 1);
for (auto i = s.size() - 1; i != 0; i = i - 2) {
s[i] = '#';
s[i - 1] = s[(i - 1) / 2];
}
s[0] = '#';
}
};参考资料:“马拉车”算法的过程解释来自 http://blog.csdn.net/dyx404514/article/details/42061017