HDU - 1560----DNA sequence

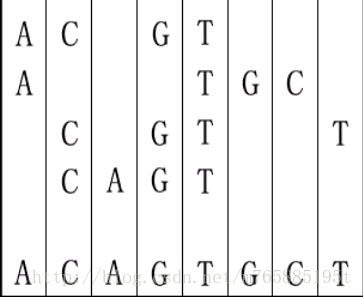
The twenty-first century is a biology-technology developing century. We know that a gene is made of DNA. The nucleotide bases from which DNA is built are A(adenine), C(cytosine), G(guanine), and T(thymine). Finding the longest common subsequence between DNA/Protein sequences is one of the basic problems in modern computational molecular biology. But this problem is a little different. Given several DNA sequences, you are asked to make a shortest sequence from them so that each of the given sequence is the subsequence of it.

For example,given”ACGT”,”ATGC”,”CGTT” and “CAGT”, you can make a sequence in the following way. It is the shortest but may be not the only one.

Input
The first line is the test case number t. Then t test cases follow. In each case, the first line is an integer n ( 1<=n<=8 ) represents number of the DNA sequences. The following k lines contain the k sequences, one per line. Assuming that the length of any sequence is between 1 and 5.

Output
For each test case, print a line containing the length of the shortest sequence that can be made from these sequences.

Sample Input
1
4
ACGT
ATGC
CGTT
CAGT
Sample Output
8

题目大意：题意就是给出N个长度不定的DNA序列，要求出一个包含这n个序列的最短序列是多长
思路：用到迭代加深搜索—–>可以参考我的这篇 非启发式搜索

#include<iostream>
#include<cstring>
#include<stdio.h>
using namespace std; 
const int N=8;

char str[N][5];
int n,ans,depth,size[N];//限制深度
char DNA[] = {'A','G','C','T'};

void DFS(int tier,int len[]){ 
    int temLen = 0;//预计还要匹配的字符串的最大长度为未匹配到的字符串长度最 
    for(int i=0 ; i<n ; i++){  
        if(size[i]-len[i] > temLen){
            temLen = size[i]-len[i]; 
        }
    }
    if(temLen == 0){//不需要匹配说明已找到 
        ans = tier;
        return;
    }
    if(tier+temLen > depth){//预计的层+已经搜的层>限制深度，停止搜索
        return;
    }

    for(int i=0 ; i<4 ; i++){
        int newLen[10];
        bool flag = false;  
        for(int j=0 ; j<n ; j++){  
            if(str[j][len[j]] == DNA[i]){//匹配到一个  
                flag = true;  
                newLen[j] = len[j]+1;//更新匹配长度  
            }else{
                newLen[j] = len[j];  
            } 
        } 
        if(flag){//没有更新匹配长度说明此情况以搜索过 
            DFS(tier+1,newLen);
        }
        if(ans != 0){//已找到答案，停止搜索 
            break;
        }
    }
}

int main(void){
    int c;
    cin>>c;

    while(c--){
        cin>>n;
        depth=0;//初始限制深度 
        for(int i=0 ; i<n ; i++){
            cin>>str[i];
            size[i] = strlen(str[i]);
            if(size[i] > depth){//初始限制深度为最长的字符串长度 
                depth = size[i];
            }
        }

        int len[N]={0};//记录了n个字符串已经匹配到的位置 
        ans = 0; 

        while(true){
            DFS(0,len);
            if(ans == 0){
                depth++;//如过没有找到答案，则搜索加深一层 
            }else{
                cout<<ans<<endl;
                break;
            }   
        }
    }

    return 0;
}