二叉搜索树详解（C++实现）

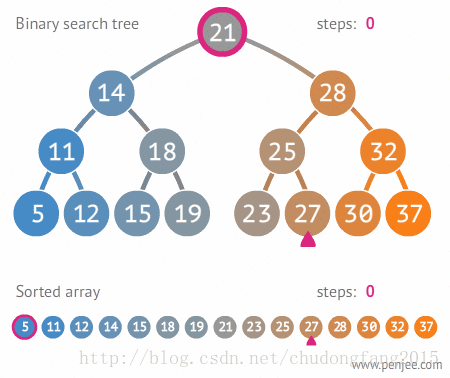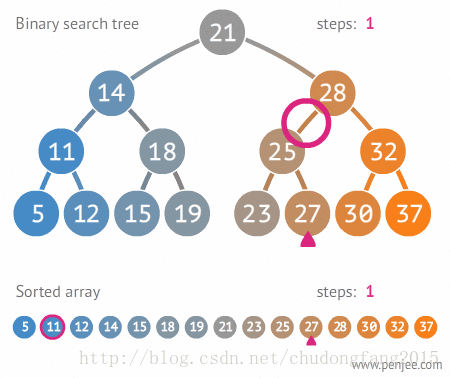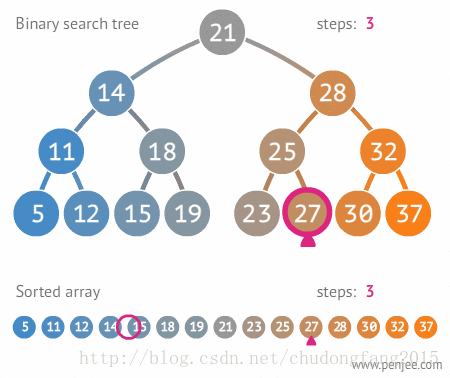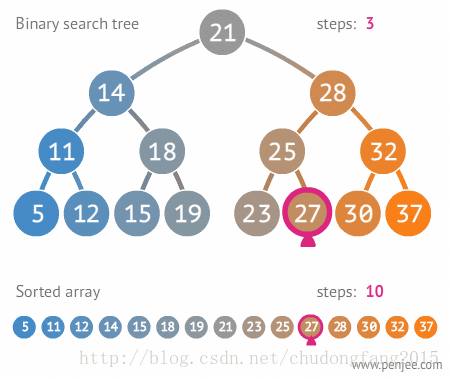
二叉搜索树的定义

二叉搜索树，也称有序二叉树,排序二叉树，是指一棵空树或者具有下列性质的二叉树：

1. 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

2. 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

3. 任意节点的左、右子树也分别为二叉查找树。

4. 没有键值相等的节点。

二叉搜索数中序遍历为有序数组

---

一、查找二叉搜索树中的某个元素

在二叉搜索树b中查找x的过程为：

• 若b是空树，则搜索失败，否则：
• 若x等于b的根节点的数据域之值，则查找成功；否则：
• 若x小于b的根节点的数据域之值，则搜索左子树；否则：
• 查找右子树。

---

二、从有序数组构造一个二叉搜索树

---

三、往二叉搜索树中插入元素

向一个二叉搜索树b中插入一个节点s的算法，过程为：

• 若b是空树，则将s所指结点作为根节点插入，否则：
• 若s->data等于b的根节点的数据域之值，则返回，否则：
• 若s->data小于b的根节点的数据域之值，则把s所指节点插入到左子树中，否则：
• 把s所指节点插入到右子树中。（新插入节点总是叶子节点）
  

---

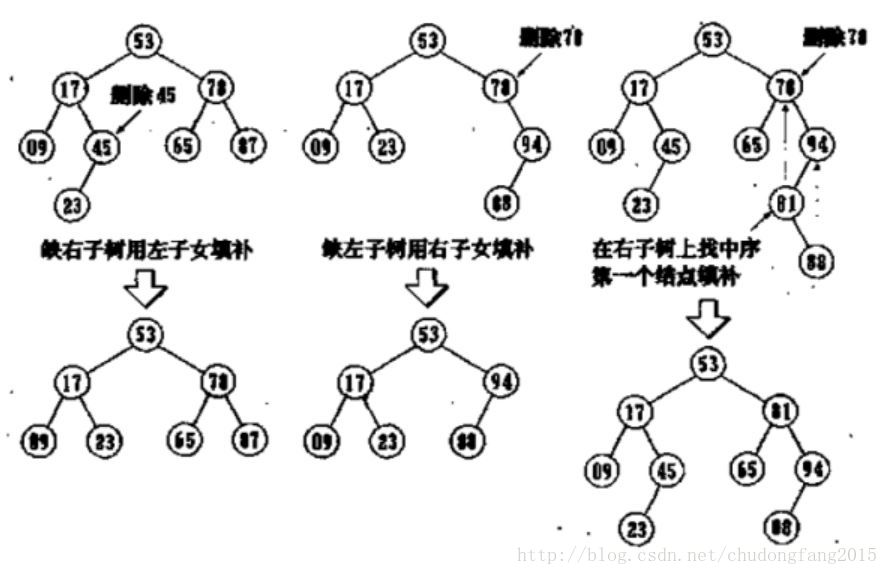
四、二叉搜索树的删除

二叉搜索树的结点删除比插入较为复杂，总体来说，结点的删除可归结为三种情况：

- 如果结点z没有孩子节点，那么只需简单地将其删除，并修改父节点，用NULL来替换z；
- 如果结点z只有一个孩子，那么将这个孩子节点提升到z的位置，并修改z的父节点，用z的孩子替换z；
- 如果结点z有2个孩子，那么查找z的后继y，此外后继一定在z的右子树中，然后让y替换z。

---

代码实现

二叉搜索树结构：

//the struct of BST
//K: the type of key
//V: the type of value
//K and V need overload operators < and > and ==
template<class K, class V>
struct BSTreeNode
{
    BSTreeNode* lchild_; //left child;
    BSTreeNode* rchild_; //right child;
    K key_;              //key
    V value_;            //value

    BSTreeNode(const K& key, const V& value) //init
        :lchild_(NULL)
        ,rchild_(NULL)
        ,key_(key)
        ,value_(value)
    {}

};

---

二叉搜索数查找：

//BST Find
Node* Find(const K& key)
{
    return Find_(root_, key);
}

Node* Find_(Node* root, const K& key)
{
    if (root == NULL)
    {
        return NULL;
    }

    if (root->key_ > key) //find in leftchild
    {
        return Find_(root->lchild_, key);
    }
    else if (root->key_ < key)//find in rightchild
    {
        return Find_(root->rchild_, key);
    }
    else
    {
        return root;
    }
}

---

二叉搜索数插入：

//BST Insert
//Find the node and Insert
bool Insert(const K& key, const V& value)
{
    return Insert_(root_, key, value);
}

bool Insert_(Node*& root, const K& key, const V& value)
{
    if (root == NULL)
    {
        root = new Node(key, value);
        return true;
    }

    if (root->key_ > key)
    {
        return Insert_(root->lchild_, key, value);
    }
    else if(root->key_ < key)
    {
        return Insert_(root->rchild_, key, value);
    }
    else
    {
        return false;
    }
}

---

二叉搜索树删除：

//BST remove
bool Remove(const K& key)
{
    return Remove_(root_, key);
}

bool Remove_(Node*& root, const K& key)
{
    //There is no such node
    if (root == NULL)
    {
        return false;
    }
    //only one node
    if (root->lchild_ == NULL&&root->rchild_ == NULL)
    {
        if (root->key_ == key)
        {
            delete root;
            root = NULL;
            return true;
        }
        else
        {
            return false;
        }

    }


    if (root->key_ > key)
    {
        Remove_(root->lchild_, key);
    }
    else if (root->key_ < key)
    {
        Remove_(root->rchild_, key);
    }
    else
    {
        Node* del = NULL;

        if (root->lchild_ == NULL)      //just has rightchild
        {
            del = root;
            root = root->rchild_;
            delete del;
            del = NULL;
            return true;
        }
        else if (root->rchild_ == NULL) //just has leftchild
        {
            del = root;
            root = root->lchild_;
            delete del;
            del = NULL;
            return true;
        }
        else
        {
            Node* RightFirst = root->rchild_;
            //find the first In order node
            while (RightFirst->lchild_)
            {
                RightFirst = RightFirst->lchild_;
            }

            //swap RightFirst node with cur node
            swap(root->key_, RightFirst->key_);
            swap(root->value_, RightFirst->value_);


            Remove_(root->rchild_, key);
            return true;
        }
    }
}

---

完整代码：

#include<bits/stdc++.h>
using namespace std;


//the struct of BST
//K: the type of key
//V: the type of value
//K and V need overload operators < and > and ==
template<class K, class V>
struct BSTreeNode
{
    BSTreeNode* lchild_; //left child;
    BSTreeNode* rchild_; //right child;
    K key_;              //key
    V value_;            //value

    BSTreeNode(const K& key, const V& value) //init
        :lchild_(NULL)
        ,rchild_(NULL)
        ,key_(key)
        ,value_(value)
    {}

};



template<class K,class V>
class BSTree
{
    typedef BSTreeNode<K, V> Node;

public:
    BSTree()
        :root_(NULL)
    {}

    //BST Find
    Node* Find(const K& key)
    {
        return Find_(root_, key);
    }

    Node* Find_(Node* root, const K& key)
    {
        if (root == NULL)
        {
            return NULL;
        }

        if (root->key_ > key) //find in leftchild
        {
            return Find_(root->lchild_, key);
        }
        else if (root->key_ < key)//find in rightchild
        {
            return Find_(root->rchild_, key);
        }
        else
        {
            return root;
        }
    }



    //BST Insert
    //Find the node and Insert
    bool Insert(const K& key, const V& value)
    {
        return Insert_(root_, key, value);
    }

    bool Insert_(Node*& root, const K& key, const V& value)
    {
        if (root == NULL)
        {
            root = new Node(key, value);
            return true;
        }

        if (root->key_ > key)
        {
            return Insert_(root->lchild_, key, value);
        }
        else if(root->key_ < key)
        {
            return Insert_(root->rchild_, key, value);
        }
        else
        {
            return false;
        }
    }



    //BST remove
    bool Remove(const K& key)
    {
        return Remove_(root_, key);
    }

    bool Remove_(Node*& root, const K& key)
    {
        //There is no such node
        if (root == NULL)
        {
            return false;
        }
        //only one node
        if (root->lchild_ == NULL&&root->rchild_ == NULL)
        {
            if (root->key_ == key)
            {
                delete root;
                root = NULL;
                return true;
            }
            else
            {
                return false;
            }

        }


        if (root->key_ > key)
        {
            Remove_(root->lchild_, key);
        }
        else if (root->key_ < key)
        {
            Remove_(root->rchild_, key);
        }
        else
        {
            Node* del = NULL;

            if (root->lchild_ == NULL)      //just has rightchild
            {
                del = root;
                root = root->rchild_;
                delete del;
                del = NULL;
                return true;
            }
            else if (root->rchild_ == NULL) //just has leftchild
            {
                del = root;
                root = root->lchild_;
                delete del;
                del = NULL;
                return true;
            }
            else
            {
                Node* RightFirst = root->rchild_;
                //find the first In order node
                while (RightFirst->lchild_)
                {
                    RightFirst = RightFirst->lchild_;
                }

                //swap RightFirst node with cur node
                swap(root->key_, RightFirst->key_);
                swap(root->value_, RightFirst->value_);


                Remove_(root->rchild_, key);
                return true;
            }
        }
    }


    //BST print In Order
    void Output()
    {
        Output_(root_);
        cout << endl;
    }

    void Output_(Node* root)
    {
        if (root == NULL)
        {
            return;
        }

        Output_(root->lchild_);
        cout << root->key_ << " ";
        Output_(root->rchild_);
    }


    Node * self()
    {
        return root_;
    }

private:
    Node* root_;
};


void Test()
{
    BSTree<int, int> s;

    //测试插入
    s.Insert(5, 1);
    s.Insert(4, 1);
    s.Insert(3, 1);
    s.Insert(6, 1);
    s.Insert(1, 1);
    s.Insert(2, 1);
    s.Insert(0, 1);
    s.Insert(9, 1);
    s.Insert(8, 1);
    s.Insert(7, 1);

    //二叉搜索树按中序输出是有序的
    s.Output();

    //测试查找
    cout << s.Find(6)->key_ << endl;

    //测试删除
    s.Remove(4);
    s.Remove(6);
    s.Remove(3);
    s.Remove(1);
    s.Remove(2);

    //再次打印删除后的结果
    s.Output();

}

int main()
{
    Test();
    return 0;
}