It's that time of the year, Felicity is around the corner and you can see people celebrating all around the Himalayan region. The Himalayan region has n gyms. The i-th gym has gi Pokemon in it. There are m distinct Pokemon types in the Himalayan region numbered from 1 to m. There is a special evolution camp set up in the fest which claims to evolve any Pokemon. The type of a Pokemon could change after evolving, subject to the constraint that if two Pokemon have the same type before evolving, they will have the same type after evolving. Also, if two Pokemon have different types before evolving, they will have different types after evolving. It is also possible that a Pokemon has the same type before and after evolving.
Formally, an evolution plan is a permutation f of {1, 2, ..., m}, such that f(x) = y means that a Pokemon of type x evolves into a Pokemon of type y.
The gym leaders are intrigued by the special evolution camp and all of them plan to evolve their Pokemons. The protocol of the mountain states that in each gym, for every type of Pokemon, the number of Pokemon of that type before evolving any Pokemon should be equal the number of Pokemon of that type after evolving all the Pokemons according to the evolution plan. They now want to find out how many distinct evolution plans exist which satisfy the protocol.
Two evolution plans f1 and f2 are distinct, if they have at least one Pokemon type evolving into a different Pokemon type in the two plans, i. e. there exists an i such that f1(i) ≠ f2(i).
Your task is to find how many distinct evolution plans are possible such that if all Pokemon in all the gyms are evolved, the number of Pokemon of each type in each of the gyms remains the same. As the answer can be large, output it modulo 109 + 7.
The first line contains two integers n and m (1 ≤ n ≤ 105, 1 ≤ m ≤ 106) — the number of gyms and the number of Pokemon types.
The next n lines contain the description of Pokemons in the gyms. The i-th of these lines begins with the integer gi (1 ≤ gi ≤ 105) — the number of Pokemon in the i-th gym. After that gi integers follow, denoting types of the Pokemons in the i-th gym. Each of these integers is between 1 and m.
The total number of Pokemons (the sum of all gi) does not exceed 5·105.
Output the number of valid evolution plans modulo 109 + 7.
2 3 2 1 2 2 2 3
1
1 3 3 1 2 3
6
2 4 2 1 2 3 2 3 4
2
2 2 3 2 2 1 2 1 2
1
3 7 2 1 2 2 3 4 3 5 6 7
24
In the first case, the only possible evolution plan is:

In the second case, any permutation of (1, 2, 3) is valid.
In the third case, there are two possible plans:

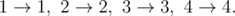
In the fourth case, the only possible evolution plan is:
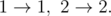
在所有gym中出现次数一样的集合 为X!(x为集合中数的数目) ,然后再相乘
#include <bits/stdc++.h>
using namespace std;
#define fo(i,s,t) for(int i = s; i <= t; ++ i)
const int MaxN = 1000050;
int n, m, g;
vector<int> a[MaxN];
int main()
{
ios::sync_with_stdio(false);
cin >>n>>m;
fo(i,1,n)
{
cin >>g;
while(g--)
{
int x;
cin>>x;
a[x].push_back(i);//统计x出现的地方
}
}
sort(a+1,a+m+1);
int t = 1;
long long ans = 1;
fo(i,2,m)
if(a[i] == a[i-1])
ans = (ans*(++t))%1000000007; else t = 1;//如果出现次数不相同,从1开始
cout <<ans<<endl;
return 0;
}