Mr. Frog’s Game

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 0 Accepted Submission(s): 0

Problem Description

One day, Mr. Frog is playing Link Game (Lian Lian Kan in Chinese).

In this game, if you can draw at most three horizontal or vertical head-and-tail-connected lines over the empty grids(the lines can be out of the whole board) to connect two non-empty grids with the same symbol or the two non-empty grids with the same symbol are adjacent, then you can change these two grids into empty and get several more seconds to continue the game.

Now, Mr. Frog starts a new game (that means there is no empty grid in the board). If there are no pair of grids that can be removed together，Mr. Frog will say ”I’m angry” and criticize you.

Mr. Frog is battle-scarred and has seen many things, so he can check the board in a very short time, maybe one second. As a Hong Kong Journalist, what you should do is to check the board more quickly than him, and then you can get out of the room before Mr. Frog being angry.

Input

The first line contains only one integer T (

T≤500), which indicates the number of test cases.

For each test case, the first line contains two integers n and m (

1≤n,m≤30).

In the next n lines, each line contains m integers, j-th number in the i-th line means the symbol on the grid(the same number means the same symbol on the grid).

Output

For each test case, there should be one line in the output.

You should output “Case #x: y”，where x is the case number(starting from 1), and y is a string representing the answer of the question. If there are at least one pair of grids that can be removed together, the y is “Yes”（without quote), else y is “No”.

Sample Input

  2 3 3 1 2 1 2 1 2 1 2 1 3 3 1 2 3 2 1 2 3 2 1
 

Sample Output

  Case #1: Yes Case #2: No 
  
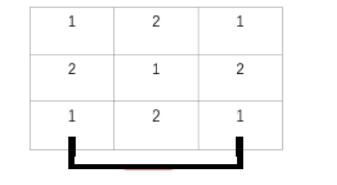
    Hint
   
 first sample can be explained as below.

Statistic | Submit | Clarifications | Back

先判断是否有相邻的，然后判断每条边是否有重复的

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <climits>
#include <cstring>
#include <string>
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <vector>
#include <list>
#define rep(i,m,n) for(i=m;i<=n;i++)
#define rsp(it,s) for(set<int>::iterator it=s.begin();it!=s.end();it++)
const int inf_int = 2e9;
const long long inf_ll = 2e18;
#define inf_add 0x3f3f3f3f
#define mod 1000000007
#define vi vector<int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define PI acos(-1.0)
#define pii pair<int,int>
#define Lson L, mid, rt<<1
#define Rson mid+1, R, rt<<1|1
const int maxn=5e2+10;
using namespace std;
typedef  long long ll;
typedef  unsigned long long  ull; 
inline int read(){int ra,fh;char rx;rx=getchar(),ra=0,fh=1;
while((rx<'0'||rx>'9')&&rx!='-')rx=getchar();if(rx=='-')
fh=-1,rx=getchar();while(rx>='0'&&rx<='9')ra*=10,ra+=rx-48,
rx=getchar();return ra*fh;}
//#pragma comment(linker, "/STACK:102400000,102400000")
ll gcd(ll p,ll q){return q==0?p:gcd(q,p%q);}
ll qpow(ll p,ll q){ll f=1;while(q){if(q&1)f=f*p;p=p*p;q>>=1;}return f;}
int dir[4][2]={{1,0},{-1,0},{0,1},{0,-1}};

map<int,int> p;
int n,m;
int a[35][35];
int main()
{
    int i,j;
    int T;
    scanf("%d",&T);
    for(int k=1;k<=T;k++)
    {
        scanf("%d %d",&n,&m);
        for(i=1;i<=n;i++)    
        {
            for(j=1;j<=n;j++)
                scanf("%d",&a[i][j]);
        }
        

        
        int flag = 1;
        for(i=1;(i<n)&&flag;i++)
        {
            for(j=1;(j<n)&&flag;j++)
            {
                if(a[i][j]==a[i+1][j]||a[i][j]==a[i][j+1])
                {
                    flag = 0;
                }
            }
        }
        
        if(flag == 0)
        {
            printf("Case #%d: Yes\n",k);
            continue;
        }
        
        
        p.erase(p.begin(),p.end());
        for(i=1;i<=n;i++)
        {
            p[a[1][i]] +=1;
            if(p[a[1][i]]>=2)
                break;
        }
        if(i!=n+1)
        {
            printf("Case #%d: Yes\n",k);
            continue;
        }
        
        p.erase(p.begin(),p.end()) ;
        for(i=1;i<=n;i++)
        {
            p[a[n][i]] ++;
            if(p[a[n][i]]>=2)
                break;
        }
        if(i!=n+1)
        {
            printf("Case #%d: Yes\n",k);
            continue;
        }
        
        p.erase(p.begin(),p.end()) ;
        for(i=1;i<=n;i++)
        {
            p[a[i][1]] ++;
            if(p[a[i][1]]>=2)
                break;
        }
        if(i!=n+1)
        {
            printf("Case #%d: Yes\n",k);
            continue;
        }
        
        p.erase(p.begin(),p.end());
        for(i=1;i<=n;i++)
        {
            p[a[i][n]] ++;
            if(p[a[i][n]]>=2)
                break;
        }
        if(i!=n+1)
        {
            printf("Case #%d: Yes\n",k);
            continue;
        }
        
        
        printf("Case #%d: No\n",k);
        
    } 
    return 0;
}