感谢出免试题过程中帮助我的各位学长以及提供思路的同学。
很荣幸成为免试题出题人之一,这次出题也算是对自己的一种磨练。第五关作为整个免试题的最后一关,主要考察点是算法的图论方面。接下来详细介绍一下第五关的通关攻略lol。
题目链接:level 5
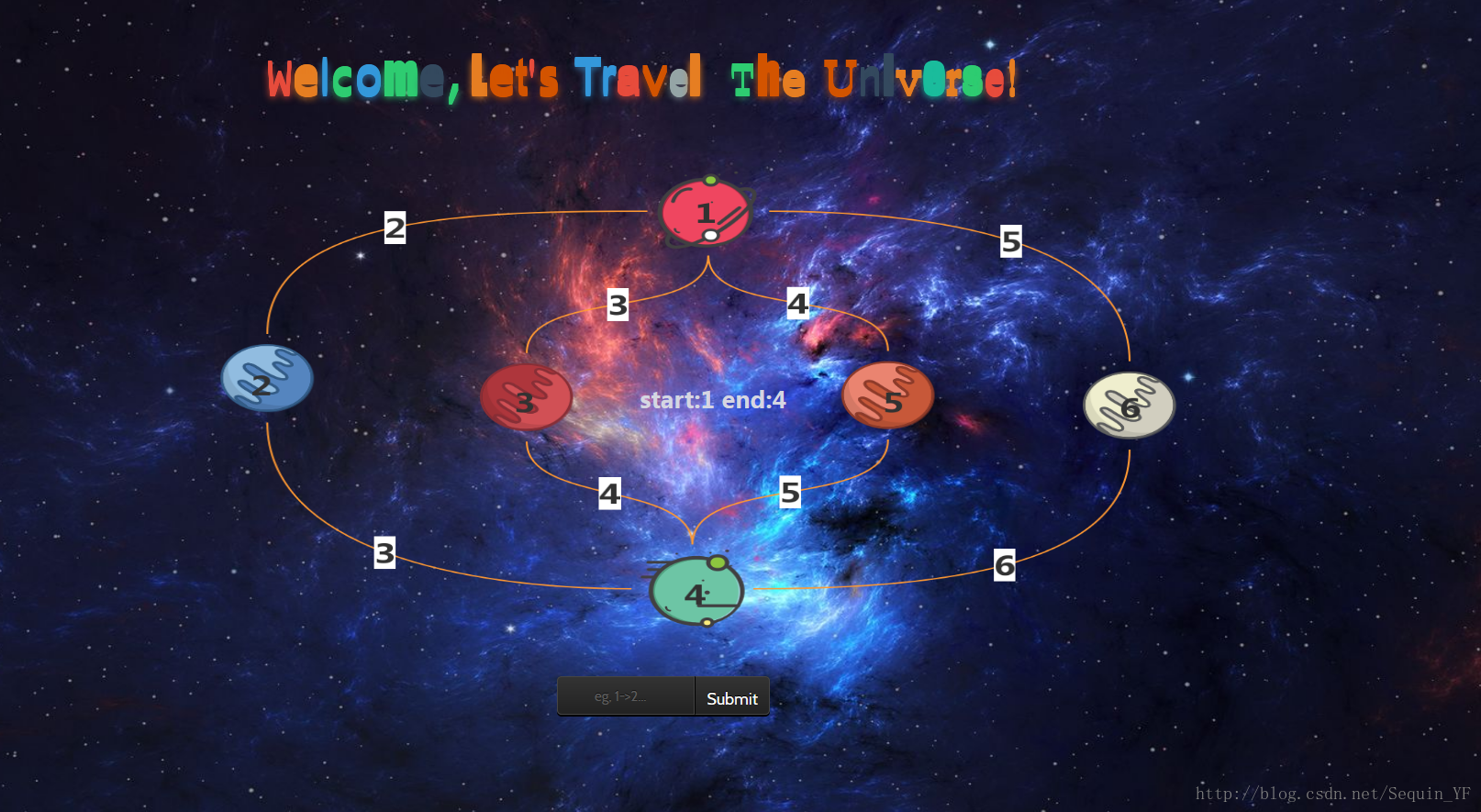
假设你现在已经通过前四关来到了最后一关,首先映入眼帘的是一些星球的连线。
相信有点图论基础的同学此时心里会大概有个方向了吧,页面上有个提交按钮还有一个start:1 end:4的提示告诉你起始点为1目标点为4。页面上暂时没有什么其他的有效信息,好在点比较少,我们可以先一个一个试一下。
对于给定的起始点和目标点来说,我们有以下四种路径:
1:1->2->4
2:1->3->4
3:1->5->4
4:1->6->4
这四条路径权值和分别为:
1->2->4 :2 + 3 = 5
1->3->4 :3 + 4 = 7
1->5->4 :4 + 5 = 9
1->6->4 :5 + 6 = 11
我们分别尝试这四条路径,发现提交1->3->4这条路径时页面跳转了,进入了第五关的第二个页面。
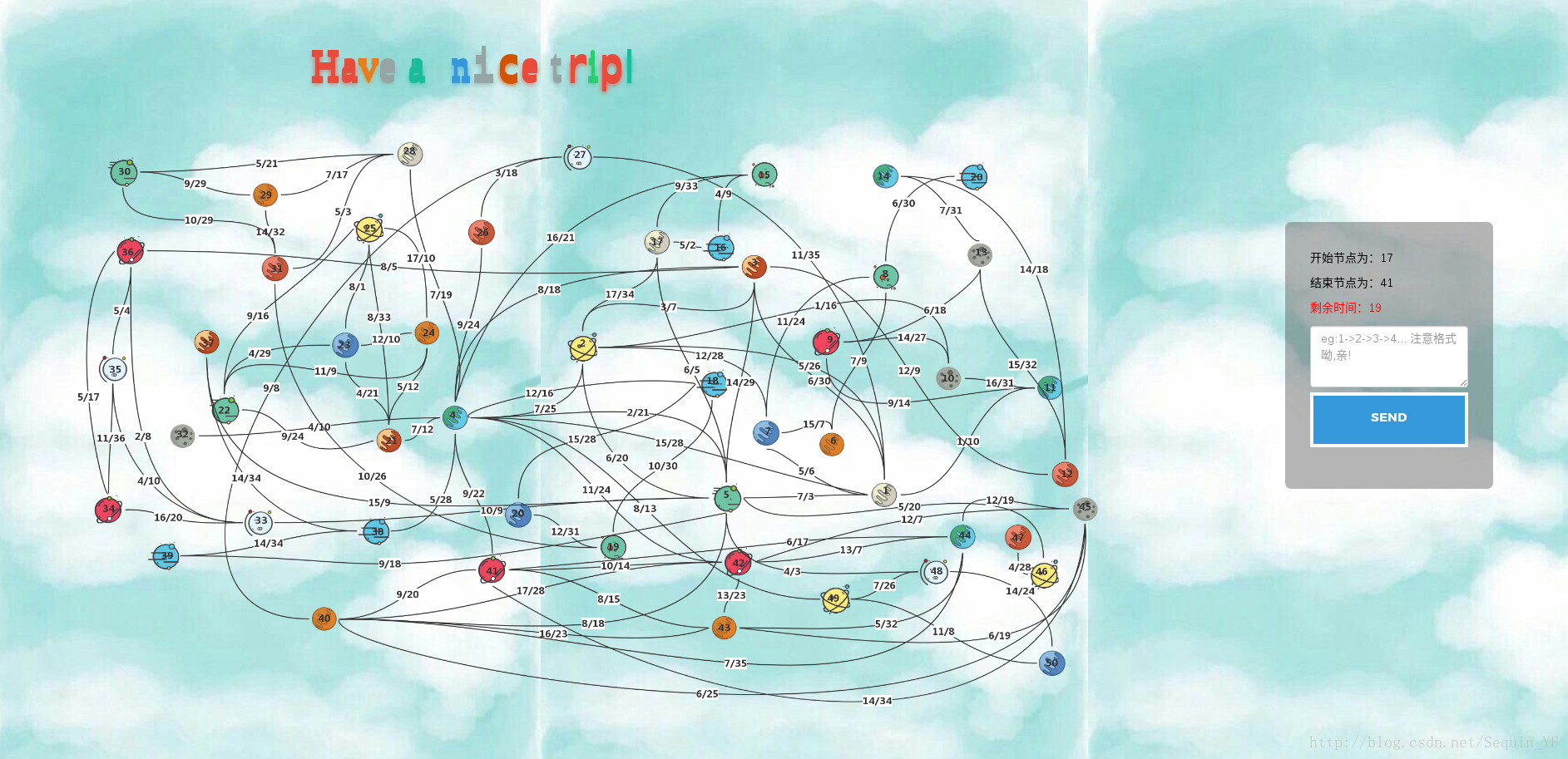
好吧,我相信在看到第二个页面的时候很多同学的内心是拒绝的O。。。我的内心也是拒绝的。。。然而再怎么吐槽这个图我也是硬着头皮画的你们也得硬着头皮做。。。ORZ
一开始拿到这个图可能会有些头大,会发现有个残忍的倒计时,但这个时候需要你们理清思路回顾以下上一个页面。在上一个页面中,我们选择1->3->4 这条路径后进入到这个页面,根据上面每条路径权值和的分析,我们发现1->3->4 是所有路径中权值和第二小的的路径。思考到这里,第五关的通关规则就很清楚了,需要你找到从起始点到目标点的次短路径。
但是这么多星球,这么多连线,自己画出来十分的麻烦,这时我们可以延续前四关的优良传统——审查元素。
这么明显的结点信息我想瞎子都能看到吧。。。赶紧先保存下来。
大概看了看,能够发现总共有50个点,97条边,每条边的权值为分数。
现在图信息有了,通关规则也有了,剩下的就是解题了。倒计时为30s,这意味着你肯定不能手动计算,还是乖乖谷歌下次短路算法吧。我们先假设你学会了次短路算法,假设你也写好了代码,假设你也得出了答案。。
#include <iostream>
#include <string.h>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#define N 205
#define MAX 0x03fffffff
using namespace std;
double Metrix[N][N];
double dist[N];
int vist[N];
int path[N];
struct edge
{
int s,t;
double cost;
}E[N];
/*
void OutPath(int s,int t,int NV)//输出路径
{
for(int i=1;i<=NV;i++)
{
}
int u=s,v=t;
while(v!=s)
{
v=path[v];
}
}
*/
int Dijkstra(int s,int t,int NV)
{
int u=s,v=t;
for(int i=1;i<=NV;i++)
{
dist[i]=MAX;
vist[i]=0;
}
for(int i=1;i<=NV;i++)
{
path[i]=s;
}
dist[u]=0;
for(int i=1;i<=NV;i++)
{
double min_value = MAX;
for(int j=1;j<=NV;j++)
{
if(vist[j]==0&&dist[j]<min_value)
{
min_value=dist[j];
u=j;
}
}
vist[u]=1;
for(int j=1;j<=NV;j++)
{
if(vist[j]==0&&dist[u]+Metrix[u][j]<dist[j])
{
dist[j]=dist[u]+Metrix[u][j];
path[j]=u;
}
}
}
if(fabs(dist[t]-MAX) < 0.000001)return -1;
return 10;
}
void SP2th(int s,int t,int NV)//NV为节点数
{
int flag=Dijkstra(s,t,NV);//求最短路
printf("%lf ", dist[t]);
if(flag==-1)
{
printf("0");
}
else
{
float min_SP=MAX;
int u=s,v=t,arcNum=0;
while(v!=u)//保存最短路到E[i]
{
E[arcNum].s=v;
E[arcNum].t=path[v];
E[arcNum].cost=Metrix[v][path[v]];
arcNum++;
v=path[v];
}
for(int i=0;i<arcNum;i++)
{ //删除E[i]
u=E[i].s;
v=E[i].t;
Metrix[u][v]=Metrix[v][u]=MAX;
flag=Dijkstra(s,t,NV);//重新计算最短路
// printf(" %lf-=-=\n", dist[t]);
if(flag==-1)
{
printf("0");
}
else
{
//OutPath(s,t,NV);
if(min_SP>dist[t])min_SP=dist[t];
}
Metrix[u][v]=Metrix[v][u]=E[i].cost;
int u = s, v = t;
while(v != u){
printf("%d->", v);
v = path[v];
}
printf("%d %lf\n",s, dist[t]);
}
printf("%lf",min_SP);
}
}
int main(int argc, char * argv[])
{
int m,n;//n为节点数,m为边数
int ss = 0;
int tt = 0;
ss= atoi(argv[1]);
tt = atoi(argv[2]);
freopen("./CASE.txt", "r", stdin);
cin >> n >> m;
int s,t;
int aa, bb;
double c = 0.0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(i==j)
{
Metrix[i][j]=MAX;
}
else
{
Metrix[i][j]=MAX;
Metrix[j][i]=MAX;
}
}
}
for(int i=0;i<m;i++)//每条路的代价
{
cin >> s >> t >> aa >> bb;
c = aa /(bb * 1.0);
if(c<=Metrix[t][s])
{
Metrix[s][t]=Metrix[t][s]=c;
}
}
SP2th(ss,tt,n);//<span style="font-family: Arial, Helvetica, sans-serif;">//求s->t的次短路</span>
return 0;
}
30秒的时间真的是有点紧,不过如果你是用程序的话还是可以来得及的,我们提交下试试
看样子是过咯~
结束的话:
通关只是目的之一,第五关作为最后一关并不是挡住所有做题的人才高兴,更重要的是希望大家能够在做题的过程中学到有用的知识,如果想要学习次短路算法,建议从学习最短路算法起步。