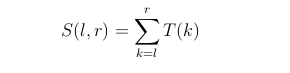Problem H 数学题
有好多人自称喜欢数学,一有数学题来了跑的比谁都快。然而,万神认为这
些人 naive ,于是出了一道数学题卡他们。题目很简单:
设 T 是 Tribonacci 数列,求
对 10 9 + 7 取模的结果。
Tribonacci 数列的定义见 http://oeis.org/A000213。
(Tribonacci numbers: a(n) = a(n-1) + a(n-2) + a(n-3) with a(0)=a(1)=a(2)=1. )
输入格式
输入文件包含多组数据(最多 100 组),请处理到文件结束。
每组数据只有 1 行,包含两个整数 l, r,用空格分割。
保证 0 ≤ l ≤ r ≤ 10 18 。
输出格式
对于每组数据输出 1 行,包含一个整数,即 S(l, r) 对 10 9 + 7 的模。
输入样例
0 2
3 5
输出样例
3
17
思想:矩阵快速幂
/**********************
> File Name: g.cpp
> Author: dulun
> Mail: dulun@xiyoulinux.org
> Created Time: 2016年04月21日 星期三 11时23分13秒
**************************/
#include<iostream>
#include<stdio.h>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#define LL long long
using namespace std;
const int N = 500086;
const LL MAX_N = 5;
const LL MOD = 1000000007;
LL N;
void mult( LL a[MAX_N][MAX_N], LL b[MAX_N][MAX_N], LL c[MAX_N][MAX_N] )
{
for( LL i = 1; i <= 4; i++ )
{
for( LL j = 1; j <= 4; j++ )
{
c[i][j] = 0;
for( LL k = 1; k <= 4; k++ )
{
c[i][j] = ( c[i][j] + a[i][k] * b[k][j] % MOD ) % MOD;
}
}
}
}
void s_pow( LL a[MAX_N][MAX_N], LL n )
{//矩阵快速幂
LL ans[MAX_N][MAX_N] = {0};
LL temp[MAX_N][MAX_N];
for( LL i = 1; i <= 4; i++ ) ans[i][i] = 1;
while( n )
{
if( n % 2 == 1 )
{
mult( ans, a, temp );
memcpy( ans, temp, sizeof( LL ) * MAX_N * MAX_N );
}
mult( a, a, temp );
memcpy( a, temp, sizeof( LL ) * MAX_N * MAX_N );
n /= 2;
}
memcpy( a, ans, sizeof( LL ) * MAX_N * MAX_N );
}
LL fuk( LL n )
{
LL a[MAX_N][MAX_N] = {0};
if( n < 0 )
{
return 0;
}
if( n == 0 )
{
return 1;
}
else if( n == 1 )
{
return 2;
}
a[1][1] = 0;a[1][2] = 1;a[1][3] = 0;a[1][4] = 0;
a[2][1] = 0;a[2][2] = 0;a[2][3] = 1;a[2][4] = 0;
a[3][1] = 1;a[3][2] = 1;a[3][3] = 1;a[3][4] = 0;
a[4][1] = 0;a[4][2] = 0;a[4][3] = 1;a[4][4] = 1;
s_pow( a, n - 1 );
LL ans = 0;
LL b[MAX_N];
b[1] = b[2] = b[3] = 1;
b[4] = 2;
for( LL i = 1; i <= 4; i++ )
{
ans = ( ans + a[4][i] * b[i] % MOD ) % MOD;
}
return ans;
}
int main()
{
LL A, B;
while( scanf( "%lld%lld", &A, &B ) != EOF )
{
printf( "%lld\n", ( fuk( B ) - fuk( A - 1 ) + MOD ) % MOD );
}
return 0;
}