定义:
回文串:一个字符串, 逆置之后,与原串相同;
回文子串: 一个字符串的子串(连续),是回文串.则该子串为整个字符串的一个回文子串.
最长回文子串:一个字符串中最长的回文子串.
求最长回文子串最容易想的
方法1(dp):
先将串逆置,再与原串求最长公共子序列(LCS)(o(n^2)), //时间O(n^2) 空间O(f(n^2));
方法2(纯暴力):
两重循环枚举起点终点(所有子串)(o(n^2)),如果是回文串,返回长度,不是返回0(o(n)),寻找最大长度.//时间 O(n^3);
稍微提升一下,
方法3(中心扩展):
枚举对称中心, 向两边扩展,遇边界,或不同,停止扩展,继续下一个对称中心,之后找最大//O(n^2);
方法4(dp):
暴力改进: 辅助数组记录从i到j是否回文
P(i,j)= P(i+1,j-1)(如果S[i] = S[j])。类动规方程。
P(i,i)= 1,P(i,i+1)= if(S[i]= S[i+1]) 个人感觉没LCS好写,好想.
下面进入正题,传说Manacher能O(n),你信吗? 反正我不信.
我看了下, 别人的博客上来就说要分奇数偶数,然后加’#’,然后谁小于等于谁,然后贴代码.
所以决定认真写下本篇博客.解除疑惑.
想写代码,首先要懂道理,看别人代码,花了好长时间看懂了,昂,是这么一回事,等让自己写原题时,能凭印象写出来,但是为什么题目稍微变一变就不会了?理解的不透彻,不深入,一定要完全弄懂道理后,自己将算法转化为代码,自己写模板,再看别人怎么写的,这样写有什么优点,再感悟,再理解,更新自己的模板,这也是鄙人的学习算法的方法.
不扯了.
首先manacher来自于中心扩展思想,所以首先要把中心扩展理解透彻.这里给出中心扩展的代码,分奇数偶数.下面写下伪代码,思路已经很清晰了,枚举中心位置,找到最长,更新最长.
//char a[N];
//cin>>a;
int find()
{
int maxlen = 0, len = strlen(a);
//--------------------------奇数-------------------------------------------
for(int i = 0; i < len; i++)
{
int l = i-1, r = i+1;
while(l >=0 && r <= len-1 && a[l] == a[r])
{
if(r-l + 1 > maxlen) maxlen = r-l+1;
l--; r++;
}
}
//-------------------------------------------------------------------------
//--------------------------偶数-------------------------------------------
for(int i = 0; i < len; i++)
{
int l = i, r = i+1;
while(l >= 0 && r <=len-1 && a[r]==a[l])
{
if(r-l+1 > maxlen) maxlen = r-l+1;
l--; r++;
}
}
//-------------------------------------------------------------------------
return maxlen;
}可以在上述代码中加上若干printf语句调试,,有没有感觉到,上述代码做了很多没必要的比较,? 好,优化!
首先是时候对奇数偶数说一声拜拜了,中心扩展,首先两个字中心!!,,偶数没有中心.所以仔细考虑一下,利用了一个很显然的数学道理
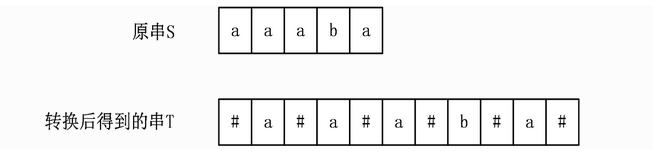
:奇数加偶数一定是奇数 ,偶数加奇数一定是奇数. 所以我们在字符串开头结尾添加#,每个字符中间加#,一共加了strlen()+1个 #
,最后得新字符串长度:2(strlen()) + 1 必为奇数. 例:我们给他加一个中心”aa” ——>”^a^a^” (#a#a#)
都可以,从而将偶数转奇数 对于奇数”a” —> “#a#” 还是奇数
观察:
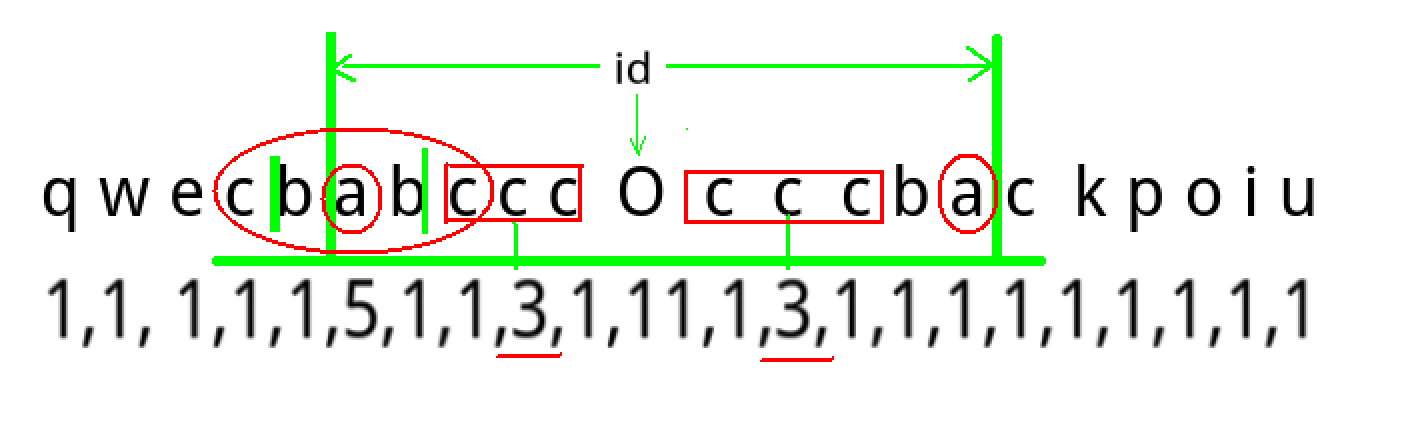
原串:qwecb abcccOcccba ckpoiu
上述代码中每次求出的l-r+1:(枚举每个字符为中心进行扩展的回文串长度) 为:
q w e c b a b c c c O c c c b a c k p o i u
1,1, 1,1,1,5,1,1,3,1,11,1,3,1,1,1,1,1,1,1,1,1 max: 11
看一下其中有没有什么空子,可不可以偷懒.
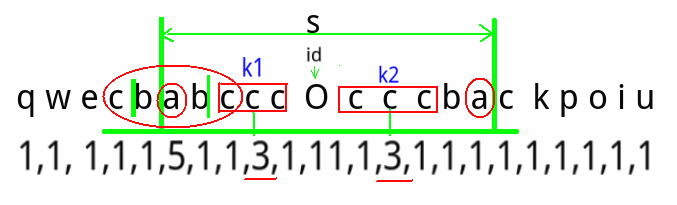
发现,对称位置有懒可以偷
k1, k2 在s(回文)之中,所以,以k1中间的c与以k2中间的c 为中心的回文子串长度必然相等..
manacher的懒就偷再这了.
(1)Len数组简介与性质
Manacher算法用一个辅助数组Len[i]表示以字符T[i]为中心的最长回文字串的最右字符到T[i]的长度,比如以T[i]为中心的最长回文字串是T[l,r],那么Len[i]=r-i+1。
对于上面的例子,可以得出Len[i]数组为:
Len
数组有一个性质,那就是Len[i]-1就是该回文子串在原字符串S中的长度,至于证明,首先在转换得到的字符串T中,所有的回文字串的长度都为奇数,那
么对于以T[i]为中心的最长回文字串,其长度就为2*Len[i]-1,经过观察可知,T中所有的回文子串,其中分隔符的数量一定比其他字符的数量多
1,也就是有Len[i]个分隔符,剩下Len[i]-1个字符来自原字符串,所以该回文串在原字符串中的长度就为Len[i]-1。
有了这个性质,那么原问题就转化为求所有的Len[i]。下面介绍如何在线性时间复杂度内求出所有的Len。
(2)Len数组的计算
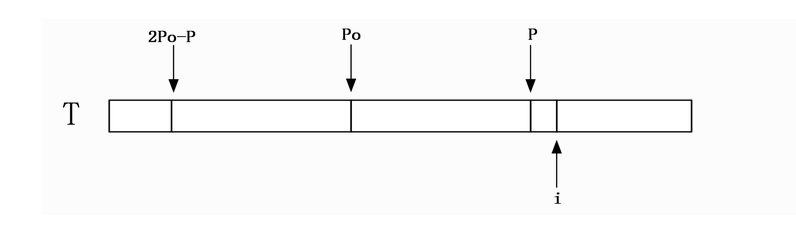
首先从左往右依次计算Len[i],当计算Len[i]时,Lenj已经计算完毕。设P为之前计算中最长回文子串的右端点的最大值,并且设取得这个最大值的位置为po,分两种情况:
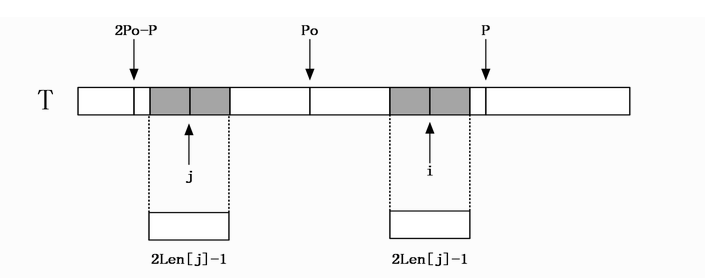
第一种情况:i<=P
那么找到i相对于po的对称位置,设为j,那么如果Len[j] < P-i,如上图: 那
么说明以j为中心的回文串一定在以po为中心的回文串的内部,且j和i关于位置po对称,由回文串的定义可知,一个回文串反过来还是一个回文串,所以以i
为中心的回文串的长度至少和以j为中心的回文串一样,即Len[i] >= Len[j]。 由对称性可知Len[i]=Len[j]。如果Len[j]>=P-i,由对称性,说明以i为中心的回文串可能会延伸到P之外,而大于P的部分我们还没有进行匹配,所以要从P+1位置开始一个一个进行匹配,直到发生失配,从而更新P和对应的po以及Len[i]。
第二种情况: i>P
如果i比P还要大,说明对于中点为i的回文串还一点都没有匹配,这个时候,就只能老老实实地一个一个匹配了,匹配完成后要更新P的位置和对应的po以及Len[i]。
题目:
hihocoder 1032 : 最长回文子串
代码:
/*************************************************************************
> File Name: 1032.cpp
> Author: dulun
> Mail: dulun@xiyoulinux.org
> Created Time: 2016年04月10日 星期日 00时52分10秒
************************************************************************/
#include<iostream>
#include<stdio.h>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#define LL long long
using namespace std;
const int N = 1e6+9;
char a[N];
char t[N*2];
int cnt[N*2];
void change()
{
int len = strlen(a);
t[0] = '@';
for(int i = 0; i < len; i++)
{
t[i*2+1] = '#';
t[i*2+2] = a[i];
}
t[len*2+1] = '#';
t[len*2+2] = '\0';
}
int manacher()
{
memset(cnt, 0, sizeof(cnt));
cnt[0] = cnt[1] = 1;
int id = 1;
int ans = 1;
int len = strlen(t);
for(int i = 2; i <= len; i++)
{
int num = min(cnt[id*2-i], cnt[id]+id-i);
while(t[i-num] == t[i+num])
num++;
cnt[i] = num;
if(id+cnt[id] < i+num)
id = i;
if(ans<num)
ans = num;
}
return ans-1;
}
int main()
{
int T;
cin>>T;
while(T--)
{
memset(t, 0, sizeof(t));
memset(a, 0, sizeof(a));
int ans;
scanf("%s", a);
change();
printf("%d\n", manacher());
}
return 0;
}
改编自:http://blog.csdn.net/dyx404514/article/details/42061017
const int maxn=1000010;
char str[maxn];//原字符串
char tmp[maxn<<1];//转换后的字符串
int Len[maxn<<1];
//转换原始串
int INIT(char *st)
{
int i,len=strlen(st);
tmp[0]='@';//字符串开头增加一个特殊字符,防止越界
for(i=1;i<=2*len;i+=2)
{
tmp[i]='#';
tmp[i+1]=st[i/2];
}
tmp[2*len+1]='#';
tmp[2*len+2]='$';//字符串结尾加一个字符,防止越界
tmp[2*len+3]=0;
return 2*len+1;//返回转换字符串的长度
}
//Manacher算法计算过程
int MANACHER(char *st,int len)
{
int mx=0,ans=0,po=0;//mx即为当前计算回文串最右边字符的最大值
for(int i=1;i<=len;i++)
{
if(mx>i)
Len[i]=min(mx-i,Len[2*po-i]);//在Len[j]和mx-i中取个小
else
Len[i]=1;//如果i>=mx,要从头开始匹配
while(st[i-Len[i]]==st[i+Len[i]])
Len[i]++;
if(Len[i]+i>mx)//若新计算的回文串右端点位置大于mx,要更新po和mx的值
{
mx=Len[i]+i;
po=i;
}
ans=max(ans,Len[i]);
}
return ans-1;//返回Len[i]中的最大值-1即为原串的最长回文子串额长度
}