题目链接 :
题目描述:
给出一个数组的区间和,如果后面与前面矛盾认为是假话
输入描述:
第一行连个整数n, m; 表示数组长度n,一共m组 之后每行三个整数,a, b, v:表示数组第a个元素到b第个元素的和为v
输出描述:
一行一个整数,表示有多少假话
思路:
1.为什么要用并查集:
在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中.....但是,这跟这题联系到一起需要一定的抽象,因为我们要判断真假,怎么判断?比较呗,怎么比?跟谁比?比什么?
首先解决怎么比,假定我们将当前输入的三个整数 : a, b, v 与 之前输入的所有a, b,
v相比,如果找到a==a&&b==b&&
v==v说明没错,但是,一定能找到吗?如果找不到,说明一定是错的吗?显然不是,所以不是这么比,要想比,首先就要找一个基准,另其为c,如果(a到c的距离)-(b到c的距离)==v,说明正确,解决了跟谁比,比什么.
基本就这个思路,
给出的是闭区间,把它换成一个半开半闭区间 (a–,b] 。半开半闭区间有个优良的性质: (a,b] + (b,c] = (a,c]
再来看这 M 条信息,对于一条信息 a,b,v 怎么解读它呢?我们可以把它解读为:a与b有关系,它们的关系有一个权值v
但是如何求ac,bc之间的距离呢,首先必须a,b的基准都为c,才可能比,怎么a,b的基准都为c呢?想到并查集是用来记录是连通关系,如果当前两点到基准点的距离,可以通过之前给出的数据推算出来,则比较,相等没事,不相等++,如果根据之前节点无法推算出当前两节点到基准的距离,说明本条信息一定正确,因为根据现有数据无法推算真假,认其为真,之后,尝试合并当前所有信息,为下一次判断做准备.
结合向量的思想,将当前a, b进行合并
现在用sum[k]表示 k 到 k基准(k的根节点) 的距离.
如果想合并a, b,最终目的是求a,b,到其共同基准的距离.首先求出a, b的祖宗,即比较标准x, y,默认x认y为爹,(a的祖先认b的祖先为爹)所以a的祖先变成了y, x的祖先变成了y,所以a到a的祖先的距离(a到y)=(a到x) + (x 到y),, b到y的距离即为sum[b]没变;
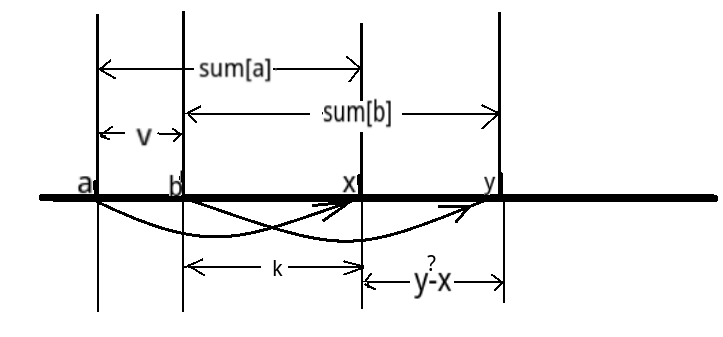
下面推倒,如图
1:sum[a] = v + k;
2:sum[b] = k + (y-x);
2-1: y-x = sum[b] - sum[a] + v;
从而另sum[x] = sum[b] - sum[a] + v; 而后更新sum[a].更新的部分放在了查找中.
@鄙人愚钝,以上纯属个人观点,还望大神指点一二.
/*************************************************************************
> File Name: hdu_3038.cpp
> Author: dulun
> Mail: dulun@xiyoulinux.org
> Created Time: 2016年03月28日 星期一 22时03分52秒
************************************************************************/
#include<iostream>
#include<stdio.h>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#define LL long long
using namespace std;
const int N = 500086;
int p[N];
int sum[N];
int find(int x)
{
if(p[x] != x)
{
int f = p[x];
p[x] = find(p[x]);
sum[x] += sum[f];
}
return p[x];
}
void init(int n)
{
for(int i = 0; i <= n; i++)
{
p[i] = i;
sum[i] = 0;
}
}
int main()
{
int n, m;
while(~scanf("%d%d", &n, &m))
{
init(n);
int ans = 0;
int a, b, v;
while(m--)
{
scanf("%d%d%d", &a, &b, &v);
a-=1;
int x = find(a);
int y = find(b);
if(x != y)
{
p[x] = y;
sum[x] = sum[b] - sum[a] + v;
}
else
{
if(sum[a] - sum[b] != v) ans++;
}
}
printf("%d\n", ans);
}
return 0;
}