题目链接:
题目描述 Description
我们都很熟悉二叉树的前序、中序、后序遍历,在数据结构中常提出这样的问题:已知一棵二叉树的前序和中序遍历,求它的后序遍历,相应的,已知一棵二叉树的后序遍历和中序遍历序列你也能求出它的前序遍历。然而给定一棵二叉树的前序和后序,你却不能确定其中序遍历序列,考虑如下图中的几棵二叉树:
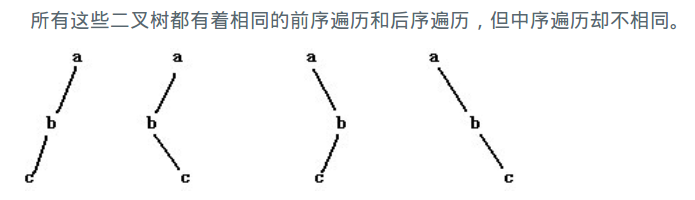
输入描述 Input Description
输入文件共2行,第一行表示该树的前序遍历结果,第二行表示该树的后序遍历结果。输入的字符集合为{a-z},长度不超过26
输出描述 Output Description
输出文件只包含一个不超过长整型的整数,表示可能的中序遍历序列的总数。
样例输入 Sample Input
abc
cba
样例输出 Sample Output
4
思路:
中序遍历的不同主要由那些只有一个儿子的结点的个数决定(连成一条线), 对于一个只有一个孩子的结点来说,他在前序和后序遍历中的位置很特殊
他在前序遍历中的后面一个结点一定是他在后序遍历前面的一个结点 (证明十分简单,可以自己考虑一下),这样就很容易找到这些点,
因为他们的孩子可能在左右两种情况,所以总个数就是2^(只有一个儿子的结点的个数)
所以只要a[i-1] == b[j] && b[j] == b[j-1] 就说明该点是一个只有一个儿子结点的结点。
/********************************************
> File Name: 1029.cpp
> Author: dulun
> Mail: dulun@xiyoulinux.org
> Created Time: 2016年03月17日 星期四 17时42分08秒
******************************************/
#include<iostream>
#include<stdio.h>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#define LL long long
using namespace std;
const int N = 50086;
char a[N];
char b[N];
int main()
{
scanf("%s%s",a, b);
int l1 = strlen(a);
int l2 = strlen(b);
int sum = 0;
for(int i = 1; i < l1; i++)
for(int j = 1; j < l2; j++)
{
if(a[i-1] == b[j] && a[i] == b[j-1])
sum++;
}
int ans = 1<<sum;
cout<<ans<<endl;
return 0;
}