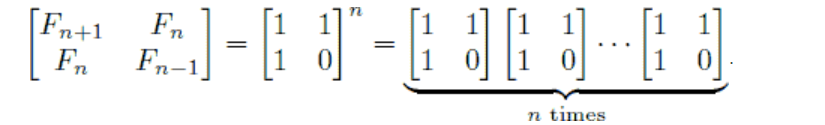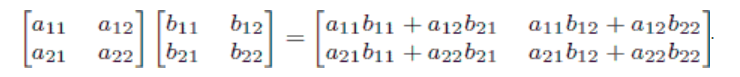51Nod 1242 斐波那契数列的第N项

题目链接：

51Nod 1242 斐波那契数列的第N项

斐波那契数列的定义如下：

F(0) = 0
F(1) = 1
F(n) = F(n - 1) + F(n - 2) (n >= 2)

(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, …)
给出n，求F(n)，由于结果很大，输出F(n) % 1000000009的结果即可。

Input

输入1个数n(1 <= n <= 10^18)。

Output

输出F(n) % 1000000009的结果。

Input示例

11

Output示例

89

矩阵快速幂,　关于快速幂，过段时间整理一篇

简单缕一下吧：相当于公式

整数快速幂伪代码：
２^32 = (2*2) ^16 = 4 ^ 16 = (4*4)^8 = (16*16) ^４;
２^31 = 2* (2*2) ^15 = ２×4×4 ^ 14 = ２×4×(4*4)^7= … //如果有跑单的，要单乘一次，使之可以二分 　o（n） ——>　o(logn)

//a的b次方:
LL ans = 1;
while(b > 0)
{
    if(b % 2 != 0) //剩一个跑单的
    {ans *= a; b--;}
    a = a * a;
    b /= 2;
}
return ans;

矩阵相乘：

/*****************************************************
    > File Name: 1242.cpp
    > Author: dulun
    > Mail: dulun@xiyoulinux.org
    > Created Time: 2016年03月16日 星期三 18时58分07秒
 *********************************************************/

#include<iostream>
#include<stdio.h>
#include<cstring>
using namespace std;
#define LL long long

const LL INF = 1000000009;

LL n;

struct Node
{
    LL c[2][2];
}t;

Node mult(Node a, Node b)
{
    Node c = {0};
    for(int i = 0; i < 2; i++)
    for(int j = 0; j < 2; j++)
    for(int k = 0; k < 2; k++)
    {
        c.c[i][j] += (a.c[i][k] * b.c[k][j]) % INF;
        c.c[i][j] %= INF;
    }
    return c;
}

Node pow(LL n)
{
    Node pt = t;
    if(n < 0) return pt;
    while(n)
    {
        if( n & 1 )
        {
            pt = mult(pt, t);
            n--;
        }
        t = mult(t, t);
        n >>= 1;
    }
    return pt;
}

int main()
{
    while(cin>>n)
    {
        t.c[0][0] = 1;
        t.c[0][1] = 1;
        t.c[1][0] = 1;
        t.c[1][1] = 0;
        Node ans = pow(n-2);
        printf("%lld\n", ans.c[0][0] * 1);
    }
    return 0;
}