问题描述
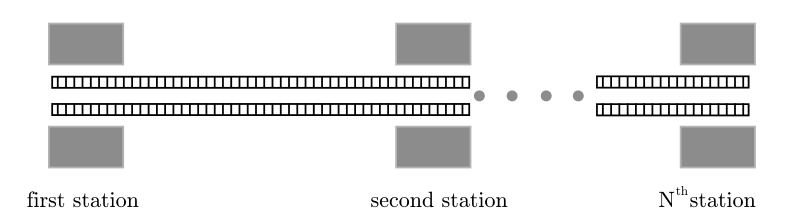
Secret agent Maria was sent to Algorithms City to carry out an
especially dangerous mission. After several thrilling events we nd
her in the rst station of Algorithms City Metro, examining the time
table. The Algorithms City Metro consists of a single line with trains
running both ways, so its time table is not complicated. Maria has an
appointment with a local spy at the last station of Algorithms City
Metro. Maria knows that a powerful organization is after her. She also
knows that while waiting at a station, she is at great risk of being
caught. To hide in a running train is much safer, so she decides to
stay in running trains as much as possible, even if this means
traveling backward and forward. Maria needs to know a schedule with
minimal waiting time at the stations that gets her to the last station
in time for her appointment. You must write a program that nds the
total waiting time in a best schedule for Maria. The Algorithms City
Metro system has N stations, consecutively numbered from 1 to N .
Trains move in both directions: from the rst station to the last
station and from the last station back to the rst station. The time
required for a train to travel between two consecutive stations is
xed since all trains move at the same speed. Trains make a very short
stop at each station, which you can ignore for simplicity. Since she
is a very fast agent, Maria can always change trains at a station even
if the trains involved stop in that station at the same time.
思路
DAG上固定起点终点的动态规划,输入,和处理较为繁琐,但思路不是特别难
/*************************************************************************
> File Name: UVa_1025_城市间谍.cpp
> Author: dulun
> Mail: dulun@xiyoulinux.org
> Created Time: 2016年03月10日 星期四 15时39分49秒
************************************************************************/
#include<iostream>
#include<stdio.h>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#define LL long long
using namespace std;
const int INF = 1<<30;
int main()
{
int kase = 0;
while(1)
{
int n, T, M1, M2;
bool has[255][255][2] = {0};
int t[255] = {0};
int d[255] = {0};
int e[255] = {0};
int ct[255] = {0};
int dp[255][255] = {0};
scanf("%d", &n);
if(n == 0) break;
scanf("%d", &T);
for(int i = 1; i <= n-1; i++) {scanf("%d", &t[i]); ct[i+1] = ct[i]+t[i];}//printf("ct[%d] = %d", i, ct[i+1]);}
ct[1] = 0;
t[n] = 0;
scanf("%d", &M1);
for(int i = 1; i <= M1; i++) scanf("%d", &d[i]);
scanf("%d", &M2);
for(int i = 1; i <= M2; i++) scanf("%d", &e[i]);
for(int i = 1; i <= M1; i++)
for(int j = 1; j <= n; j++) has[d[i]+ct[j]][j][0] = 1;
for(int i = 1; i <= M2; i++)
for(int j = 1; j <= n; j++) has[e[i]+ct[n]-ct[n-j+1]][n-j+1][1] = 1;
for(int i = 1; i < n; i++) dp[T][i] = INF;
dp[T][n] = 0;
for(int i = T-1; i >= 0; i--)
for(int j = 1; j <= n; j++)
{
dp[i][j] = dp[i+1][j] + 1;
if( j < n && has[i][j][0] && i+t[j] <= T) dp[i][j] = min(dp[i][j], dp[i+t[j]][j+1]);
if( j > 1 && has[i][j][1] && i+t[j-1] <= T) dp[i][j] = min(dp[i][j], dp[i+t[j-1]][j-1]);
}
printf("Case Number %d: ", ++kase);
if(dp[0][1] >= INF) printf("impossible\n");
else printf("%d\n", dp[0][1]);
}
return 0;
}