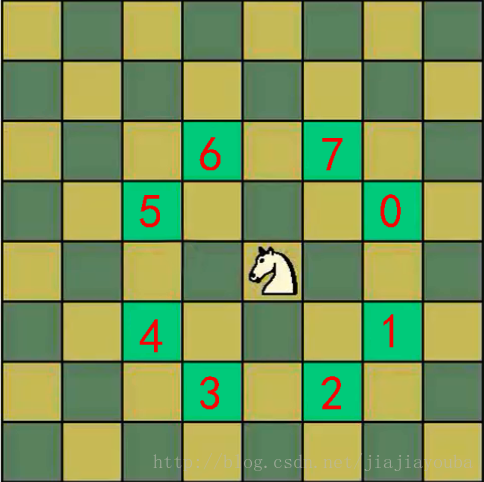
马踏棋盘算法(骑士周游问题)
定义:将马随机放在国际象棋的8×8棋盘[0~7][0~7]的某个方格中,马按走棋规则进行移动。要求每个方格只进入一次,走遍棋盘上全部64个方格
(可扩展为NxN的棋盘)
鄙人小白,连续数天研究此问题。
也是老师布置的作业,某老师编写的教科书上面的代码思想为:
采用栈的数据结构,即将马的行走顺序压入栈中
具体步骤如下:
1)建立一个栈,定义其栈顶和栈底,以及栈的大小。
2)将马的初始步压入栈中,计算其8个方向的权值,各点的8个方向按权值升序排列。
3)马向最小权值方向行走,得到下一步,重复步骤(2)
4)某步的下一步超出棋盘,则应重新走,这一步出栈,由前一步重新选择方向。
5)最后,根据栈中内容将马的行走路线填入方阵中,输出
其中栈的作用就是保存马的路径,以便走错了之后“回溯”(悔棋)用
一开始并不明白是怎么回事,于是百度
方法一:深搜+回溯
找到了深搜+回溯的方法,思想就是一直在找下一个可以糟蹋的点,糟蹋后再找下一个点,同一个点只能走一次。
自己写代码如下:
主要函数及功能:
1)int NextStep(int *x, int *y , int step)找下一个可以糟蹋的点,参数为地址值,函数调用后,x,y值已经成为下一个点。
2)int Dfs(int x, int y, int count)深搜方法不断地往下一个走,直到踏遍所有点。
/*************************************************************************
> File Name: mataqipan.c
> Author:***
> Mail: ***
> Created Time: Fri 09 Oct 2015 02:27:36 PM EDT
************************************************************************/
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#define N 8
int CHESS[N][N];
int NextStep(int *x, int *y , int step)
{
switch(step)
{
case 0:
{
if(*x + 1 <= N -1 && *y - 2 >= 0 && CHESS[*x +1][*y -2] == 0)
{
*x = *x + 1;
*y = *y - 2;
return 1;
}
break;
}
case 1:
{
if(*x + 1 <= N -1 && *y + 2 <= N -1 && CHESS[*x +1][*y+2] == 0)
{
*x = *x + 1;
*y = *y + 2;
return 1;
}
break;
}
case 2:
{
if(*x + 2 <= N -1 && *y - 1 >= 0 && CHESS[*x+2][*y -1] == 0)
{
*x = *x + 2;
*y = *y - 1;
return 1;
}
break;
}
case 3:
{
if(*x + 2 <= N -1 && *y + 1 <= N -1 && CHESS[*x +2][*y +1] == 0)
{
*x = *x + 2;
*y = *y + 1;
return 1;
}
break;
}
case 4:
{
if(*x - 1 >= 0 && *y - 2 >= 0 && CHESS[*x-1][*y -2] == 0)
{
*x = *x - 1;
*y = *y - 2;
return 1;
}
break;
}
case 5:
{
if(*x - 1 >= 0 && *y + 2 <= N -1 && CHESS[*x - 1][*y + 2] == 0)
{
*x = *x - 1;
*y = *y + 2;
return 1;
}
break;
}
case 6:
{
if(*x - 2 >= 0 && *y - 1 >= 0 && CHESS[*x-2][*y-1 ] == 0)
{
*x = *x - 2;
*y = *y - 1;
return 1;
}
break;
}
case 7:
{
if(*x - 2 >= 0 && *y + 1 <= N -1 && CHESS[*x -2][*y + 1] == 0)
{
*x = *x - 2;
*y = *y + 1;
return 1;
}
break;
}
default:
break;
}
return 0;
}
//深搜遍历
int Dfs(int x, int y, int count)
{
int x1 = x;
int y1 = y;
int flag = 0;
int result , i;
if(count > N * N )//出口,全部遍历
{
return 1;
}
for(i = 0; i < 8 ; i++ )
{
flag = NextStep(&x1, &y1, i);
printf("%d\n", flag);
if( 1 == flag)
{
CHESS[x1][y1] = count;
result = Dfs(x1, y1, count+1);//递归调用
if(result)
{
return 1;
}
else{
CHESS[x1][y1] = 0;
x1 = x;
y1 = y;
}
}
}
return 0;
}
void Print()
{
int i, j;
for(i = 0; i < N ;i++)
{
for(j = 0; j < N; j++)
{
printf("%5d", CHESS[i][j]);
}
printf("\n\n");
}
printf("\n\n");
}
int main()
{
clock_t start, end;
int i, j, result;
for(i = 0; i < N; i++) //初始化棋盘
{
for(j = 0; j < N; j++)
{
CHESS[i][j] = 0;
}
}
printf("请输入起始x:");
scanf("%d", &i);
printf("请输入起始y:");
scanf("%d", &j);
if(i < 0 || i > 7 || j < 0 || j > 7)
{
printf("输入错误,请重新输入\n");
return 0;
}
start = clock();
CHESS[i][j] = 1;
result = Dfs(i,j,2);
printf("result = %d\n", result);
end = clock();
Print();
return 0;
}这个思想简单易想,不过耗时很久,与起始点有关,有的10分钟,有的一夜都跑不出来。
方法二:贪心算法(不回溯)
于是又找了贪心算法的例子,基本思想:
在马的当前位置找下一个位置,并确定下一个位置有几个可以糟蹋的位置,比较难理解,说白了就是每一步要确定要走的下几步分别有几种走法,然后按走法最少的方向走,因为在棋盘边缘的位置下一个可走的位置一定是比棋盘中间少的,所以马儿基本是按照先把棋盘靠边缘的位置糟蹋一遍,再糟蹋中间的棋盘的路线踏满整个棋盘的,所以每次向下一步走法最少的点走肯定是没有错的,但是经过实验,按照这种思想走下去一定能踏满整个棋盘,不需要回头,笔者也实验了很多奇葩的点,对角线,定点,边缘,都可以顺利踏满棋盘。但是即使是当前来看最小的点,走过去以后也有可能存在不能踏满整个棋盘的情况,这种情况是存在的,因为每次只考虑下一次,并没有从整体上考虑。“只要下一步走到当前点能走的下几步中的下一步最少的那个当前点的下一步,就最能踏满全部点”亲测这种方法8*8有两个点踏不出来 有点拗口,仔细体会一下好像是这回事。并不需要回溯。各位自己体会
代码如下:
/*************************************************************************
> File Name: mataqipan.c
> Author:
> Mail:
> Created Time: Fri 09 Oct 2015 02:27:36 PM EDT
************************************************************************/
#include<stdio.h>
#include<time.h>
#define N 8
int CHESS[N][N];
typedef struct
{
int x, y;
int waysout;
}Node;
int dx[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[8] = {1, 2, 2, 1, -1, -2, -2, -1};
void dfs(int x, int y, int count);
void Print();
void sortnode(Node *hn, int n);
int ways_out(int x, int y);
int ways_out(int x, int y)
{
int i, count = 0;
int x1, y1;
if(x < 0 || y <0 || x >= N || y >= N || CHESS[x][y] > 0)
{
return -1;
}
for(i = 0; i < 8; i++)
{
x1 = x + dx[i];
y1 = y + dy[i];
if(x1 < 0 || y1 < 0 || x1 >=N || y1 >= N )
{
continue;
}
if(0 == CHESS[x1][y1])
{
count += 1;
}
}
return count;
}
//深搜遍历
void dfs(int x, int y, int count)
{
int i, x1, y1;
Node hn[8];
if(count > N * N )//出口,全部遍历
{
//printf("count = %d\n\n\n\n\n\n\n", count);
Print();
return ;
}
for(i = 0; i < 8 ; i++ )
{
hn[i].x = x1 = x + dx[i];
hn[i].y = y1 = y + dy[i];
hn[i].waysout = ways_out(x1, y1);
}
sortnode(hn, 8);
for(i = 0; hn[i].waysout < 0; ++i);
for(; i < 8; ++i)
{
x1 = hn[i].x;
y1 = hn[i].y;
CHESS[x1][y1] = count;
dfs(x1, y1, count + 1);
}
}
void Print()
{
int i, j;
for(i = 0; i < N ;i++)
{
for(j = 0; j < N; j++)
{
printf("%5d", CHESS[i][j]);
}
printf("\n\n");
}
printf("\n\n");
}
void sortnode(Node *hn, int n)
{
int i, j, t;
Node temp;
for(i = 0; i < n ; ++i)
{
for(t = i, j = i + 1; j < n; ++j)
{
if(hn[j].waysout < hn[t].waysout)
{
t = j;
}
}
if(t > i)
{
temp = hn[i];
hn[i] = hn[t];
hn[t] = temp;
}
}
}
int main()
{
clock_t start, end;
int i, j, result = 0;
int x, y;
for(i = 0; i < N; i++) //初始化棋盘
{
for(j = 0; j < N; j++)
{
CHESS[i][j] = 0;
}
}
printf("请输入起始x(0-%d):", N -1);
scanf("%d", &x);
printf("请输入起始y:(0-%d):", N -1);
scanf("%d", &y);
if(x < 0 || y < 0 || x >= N|| y >= N)
{
printf("输入错误,请重新输入\n");
return 0;
}
start = clock();
CHESS[x][y] = 1;
dfs(x,y,2);
end = clock();
printf("共用时 %fs\n\n", (double)(end -start) / 1000 );
return 0;
}方法三:采用栈的数据结构
好吧,我们回归教材,根据上面的经验,回头看书上的思想,如本文开篇所述。
经过改编,结合同学的代码,用书上的代码实现一下