选择类排序---堆排序

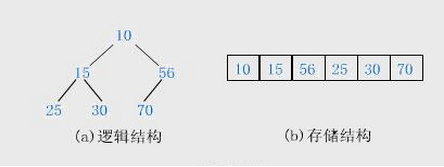
堆存储：

堆的数据实际是保存在数组中的，i结点的父结点下标就为(i – 1) / 2。它的左右子结点下标分别为2 * i + 1和2 * i + 2。如第0个结点左右子结点下标分别为1和2。使用数组进行存储，使用完全二叉树作为分析结构。

大根堆：根节点的值大于等于左右子树的值
小根堆：根节点的值小于等于左右子树的值

堆排序主要有几个操作步骤：

1> 初始化堆：先将一个数组初始化为一颗完全二叉树，再利用筛选的方法逐层向上把所有子树调整为大根堆（小根堆）。

2> 取出根节点的值，最后一个叶子节点的值赋予根节点，再次调节堆为大根堆（小根堆）。

/*======================================================
    > File Name: heapSortSelf.c
    > Author: panlu
    > E-mail: view@xiyoulinux.org
    > Other : 堆排序 
    > Created Time: 2015年12月15日 星期二 21时51分18秒
 =======================================================*/

#include<stdio.h>
#define Lchild(i)  (2*i+1)            //某个节点的左子树节点位置
#define Rchild(i)  (2*i+2)            //某个节点的右子树节点位置

void swap(int *i,int *j){
    int temp = *i;
    *i = *j;
    *j = temp;
}

void heapLittle(int *array,int length,int current_node){             //只是进行小根堆的初始化,current_node是当前数字在数组中的下标
    int l_child = Lchild(current_node);
    int r_child = Rchild(current_node);
    int min = current_node;
    if(array[current_node] > array[l_child] && l_child < length){    //若左子树的值比自己的小，则把左子树提上去
       swap(array+current_node,array+l_child);
       min = l_child;                                                
    }
    if(array[current_node] > array[r_child] && r_child < length){
        swap(array+current_node,array+r_child);
        min = r_child;
    }
    if(min!=current_node){
        heapLittle(array,length,l_child);                            //发现有改动之后就把该节点的左子树下面再进行调整
        heapLittle(array,length,r_child);                            //调整右子树
    }
}

void initHeap(int *array,int length){                                 //将数组改造成堆
    int i = length/2-1;                                               //从第一个非叶子节点开始往上继续调整
    for(; i >= 0; i--){                                               
        heapLittle(array,length,i);
    }
}

void heapSort(int *array,int length){
    int cur = length-1;
    array[0] = array[cur];
    initHeap(array,cur);
} 

int main(){
    int length;
    int i = 0;
    int array[20];
    printf("请输入数组的长度: ");
    scanf("%d",&length);
    printf("请输入数组的值: \n");
    for(; i < length; i++){
        scanf("%d",array+i);
    }
    initHeap(array,length);

    for(i =0 ; i< length; i++){
        printf("%d ",array[i]);
    }

    printf("\n-------aftersort-------");
    printf("\n");
    for(i = length; i > 0; i--){
        printf("%d ",array[0]); //循环取出根节点的值
        heapSort(array,i);
    }
}