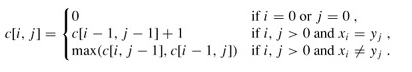一.基本概念
最长公共子串:子串在原字符串中是最长且连续的.
最长公共子序列:子串在原字符串中是最长且可以不连续的.
二.解题步骤
按照上一篇动态规划的解题步骤:
1)找出最长公共子序列的结构
设序列X = {x1,x2,…xm}和Y = {y1,y2,…yn}的最长公共子序列为Z = {z1,z2,…zk},则:
若Xm = Yn,则Zk = Xm = Yn,且Zk-1是Xk-1和Yk-1的最长公共子序列
若Xm != Yn 且Zk != Xm ,则Z是Xm-1和Y的最长公共子序列
若Xm != Yn 且Zk != Yn ,则Z是X和Yn-1的最长公共子序列
2)写出子问题的递归结构
3)计算最优值
我们用C[i][j]存储X[i]和Y[j]的最长公共子序列长度,
B[i][j]记录C[i][j]的值是由哪一个子问题解到的,在构造最长公共子序列时由其得到最长公共子串的解.
void LCSLength(int m,int n,char *x,char *y,int c[][MAXLEN],int b[][MAXLEN]){
int i,j;
for(i = 0; i <=m; i++) c[i][0]=0;
for(i = 1; i <=n; i++) c[0][i]=0;
for(i = 1; i <= m; i++){
for(j = 1; j <= n; j++){
//注意x序列和c数组下标相差1
if(x[i-1]==y[j-1]){
c[i][j]=c[i-1][j-1]+1;
b[i][j]=1;
}else if(c[i-1][j]>c[i][j-1]){
c[i][j]=c[i-1][j];
b[i][j]=2;
}else{
c[i][j]=c[i][j-1];
b[i][j]=3;
}
}
}
}4)构造最长公共子串
利用回溯的方法,首先从B[i][j]开始,
当B[i][j]=1时,表示Xi和Yj的最长公共子序列是由Xi-1和Yj-1的最长公共子序列加上Xi所得;
当B[i][j]=2时,表示Xi和Yj的最长公共子序列和Xi-1和Yj的最长公共子序列相同;
当B[i][j]=3时,表示Xi和Yj的最长公共子序列和Xi和Yj-1的最长公共子序列相同;
void LCS(int i, int j, char *x,int b[][MAXLEN]){
if(i==0||j==0) {return;}
if(b[i][j]==1){
LCS(i-1,j-1,x,b);
//注意x序列和c数组下标相差1
printf("%c ",x[i-1]);
}else if(b[i][j]==2){
LCS(i-1,j,x,b);
}else{
LCS(i,j-1,x,b);
}
}编辑距离问题与此有异曲同工之妙,可以一起做一下.