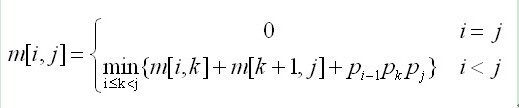矩阵连乘问题—–动态规划
- 算法思想:
- 给定n个矩阵{A1,A2,……..An},相连的两个矩阵满足矩阵连成的的条件,计算矩阵连乘乘积的计算次序,使得依此次序计算矩阵连乘需要的数乘的次数最少.
- 找出最优解的性质,刻画其特征结构
对于矩阵连乘问题,最优解就是找到一种计算顺序,使得计算次数最少.
设m[i][j]为从第i个矩阵到第j个矩阵相乘的最优解(记为A[i:j). 假设这个最优解是从第k个矩阵断开i<=k<=j,那么A[i,k]和A[k+1,j]也是相应矩阵连乘的最优解。 - 建立递归关系
- 设计算A[i:j],1<=i<=j<=n;所需要的最少数乘次数m[i][j],则整个问题的最优解就是m[i][n];
- 当i==j时,即m[i][i]代表一个矩阵,不会和其它矩阵相乘,所以乘的次数为0次,所以m[i][i],即m矩阵的对角线值都为0;
- 当i < j时,m[i][j]=min{m[i][k]+m[k+1,j]+pi-1*pk*pj} ; (相当于把i~j这j-i个矩阵分成两段,看哪种分法的次数最少),
在这里,我们用s[i][j]来表示第i个矩阵到到第j个矩阵连乘在哪个矩阵后面断开能得到最优解。
注意:上面的的算法分析没有用到数组的0号下标,下面的程序用到了0号下标.即(m[0][1])代表的是第一个矩阵和第二个矩阵相乘.
看代码:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
int matrix_chain(int *p,int n,int **m,int **s)
{
int i,j,r,k;
for(i=0;i<n;i++){
m[i][i]=0;
}
//r为连成矩阵的个数.
for(r=2;r<=n;r++){
//i表示r个矩阵连乘的第一个
for(i=0;i<=n-r;i++){
j=i+r-1;
//m[i][j]=65535;
//在第一个与最后一个之间寻找最合适的断开点.
m[i][j]=m[i+1][j]+p[i]*p[i+1]*p[j];
s[i][j]=i;
for(k=i+1;k<=j-1;k++){
int tmp=m[i][k]+m[k+1][j]+p[i]*p[k+1]*p[j+1];
if(tmp < m[i][j]){
m[i][j]=tmp;
s[i][j]=k;
}
}
}
}
}
print_chain(int i, int j, char **a,int **s)
{ //递归的方式来把最小乘数的表达式输出
if (i == j)
{
printf("%s",a[i]);
}
else
{
printf("(");
print_chain(i,s[i][j],a,s);
print_chain(s[i][j]+1,j,a,s);
printf(")");
}
}
int main(int argc,char *argv[])
{
int *p,**min_part,**min_point;
char **a;
int n=6,i,j;
int ret;
p=(int *)malloc(sizeof(int)*(n+1));
a=(char **)malloc(n*sizeof(char *));
min_part=(int **)malloc(n*sizeof(int *));
min_point=(int **)malloc(n*sizeof(int *));
for( i=0;i<n;i++){
min_part[i]=(int *)malloc(n*sizeof(int));
min_point[i]=(int *)malloc(n*sizeof(int));
a[i]=(char *)malloc(n*sizeof(char));
}
p[0]=30;
p[1]=35;
p[2]=15;
p[3]=5;
p[4]=10;
p[5]=20;
p[6]=25;
a[0]="A1";
a[1]="A2";
a[2]="A3";
a[3]="A4";
a[4]="A5";
a[5]="A6";
ret=matrix_chain(p,n,min_part,min_point);
printf("Minest times: %d\n",ret);
print_chain(0,n-1,a,min_point);
printf("\n");
printf("打印min_point\n");
for(i=0;i<6;i++){
for(j=0;j<6;j++){
printf("%d ",min_point[i][j]);
}
printf("\n");
}
printf("打印min_part\n");
for(i=0;i<6;i++){
for(j=0;j<6;j++){
printf("%d ",min_part[i][j]);
}
printf("\n");
}
free(p);
free(min_part);
free(min_point);
free(a);
return 0;
}