1.概念

赫夫曼树

赫夫曼树,又称最优树，是一类带权路径长度最短的树。
首先给出路径和路径长度的概念。从树中一个节点到另一个节点之间的分支构成这两个节点之间的路径，路径上的分支数目叫做路径长度。树的路径长度是从树根到每一节点的路径长度之和。
考虑上带权的节点。节点的带权路径长度为从该结点到树根之间的路径长度与节点上权的乘积。树的带权路径长度为树中所有叶子节点的带权路径长度之和，通常记作WPL= $\sum_{k=0}^n$ w_kl_k 。
举个例子，如下图
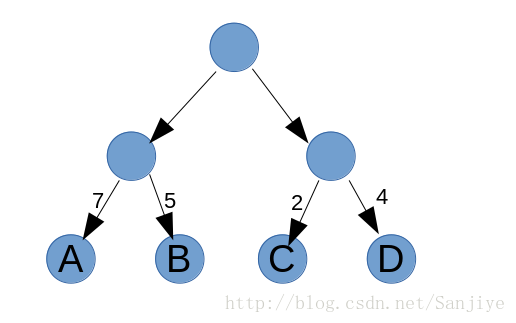
这里写图片描述
WPL=7*2+5*2+2*2+4*2=36
上图中的树不是赫夫曼树，由7，5，2，4构成的赫夫曼树如图所示

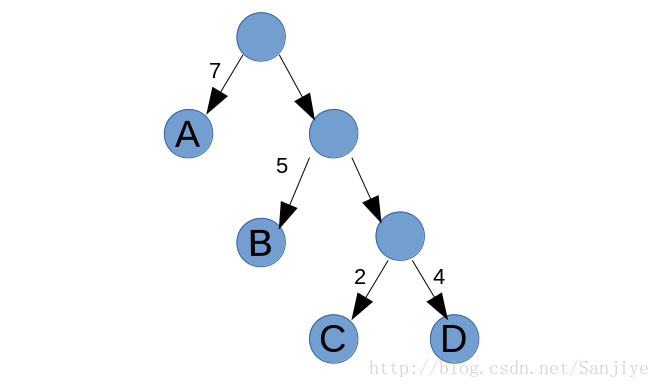
WPL=7*1+5*2+2*3+4*3

赫夫曼编码

按照上面的赫夫曼树，我们将在父节点左边的路径用0表示，右边的用1表示。由此得到
A (0)
B (10)
C (110)
D (111)
这样的二进制编码我们称为赫夫曼编码。

赫夫曼树算法分析

1.根据给定的n个权值构成n棵二叉树的合集F。（每棵二叉树的左右子树为空）
2.在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树，且置新的二叉树的根结点的权值为其左右子树上根结点的权值之和。
3.在F中删除这两棵树，同时将新得到的二叉树加入F中。
4.重复步骤2和步骤3，直到F中只剩一棵树为指。这棵树便是赫夫曼树。

代码

#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<limits.h>

typedef struct Tree              //创建一个树结构
{
    int weight;   //权值
    int left;     //左子树
    int right;    //右子数
    int flag;     //标记，用来鉴定是否使用
    int parent;   //父节点
}HaffTree;

void CreateHaffTree(int* weight,int n,HaffTree* pHaffTree)    //创建赫夫曼树
{
    int i,j,min1,min2,x1,x2;   //min1,min2分别为最小值和次最小值，x1,x2分别为最小值和次最小值对应下标
    for(i=0;i<2*n-1;i++)       //初始化HaffTree
    {
        if(i<n)
            pHaffTree[i].weight=weight[i];
        else
            pHaffTree[i].weight=0;
        pHaffTree[i].left=0;
        pHaffTree[i].right=0;
        pHaffTree[i].flag=0;    //未使用的初始化为0
        pHaffTree[i].parent=0;
    }
    for(i=0;i<n-1;++i)
    {
        min1=min2=INT_MAX;    //INT_MAX对应头文件为limits.h
        x1=x2=0;
        for(j=0;j<n+i;++j)
        {
            if(pHaffTree[j].weight<min1&&pHaffTree[j].flag==0)  
            {
                min2=min1;
                x2=x1;
                min1=pHaffTree[j].weight;
                                x1=j;
            }
            else if(pHaffTree[j].weight<min2&&pHaffTree[j].flag==0)
            {
                min2=pHaffTree[j].weight;
                x2=j;
            }
        }
        pHaffTree[x1].flag=1;
        pHaffTree[x2].flag=1;
        pHaffTree[x1].parent=pHaffTree[x2].parent=n+i;
        pHaffTree[n+i].weight=min1+min2;
        pHaffTree[n+i].left=x1;
        pHaffTree[n+i].right=x2;
    }
}
void HaffCode(HaffTree* pHaffTree,int n,char*** code)   //根据赫夫曼树求赫夫曼码，由叶子到根求赫夫曼编码，因此start--
{
    int i;
    char ch[20]="";
    int start;
    int parent;
    int child;
    int len;
    *code=(char**)malloc(sizeof(char**)*n);
    for(i=0;i<n;++i)
    {
        parent=pHaffTree[i].parent;
        child=i;
        start=18;
        while(parent!=0)
        {
            if(pHaffTree[parent].left==child)
                ch[start--]='0';
            else
                ch[start--]='1';
            child=parent;
            parent=pHaffTree[parent].parent;
        }
        len=strlen(ch+start+1)+1;
        (*code)[i]=(char*)malloc(len);
        strcpy((*code)[i],ch+start+1);
    }

}

void main()
{
    int weight[]={7,5,2,4};
    int n=sizeof(weight)/sizeof(int);
    HaffTree* pHaffTree=(HaffTree*)malloc(sizeof(HaffTree)*(2*n-1));  //有n个叶子节点，因此总节点个数为2n-1
    CreateHaffTree(weight,n,pHaffTree);
    char** code=NULL;
    HaffCode(pHaffTree,n,&code);
    for(int i=0;i<n;++i)
    {
        printf("%d ",weight[i]);
        puts(code[i]);
    }
}

看看结果吧
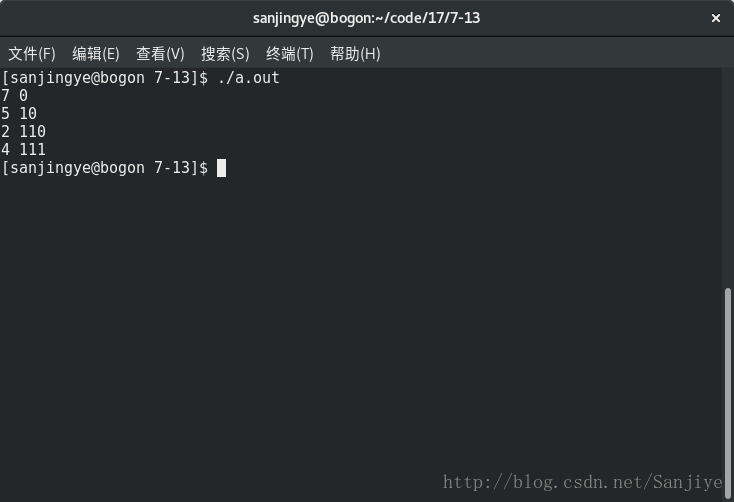
这里写图片描述
和根据赫夫曼树中推出的结果一样。