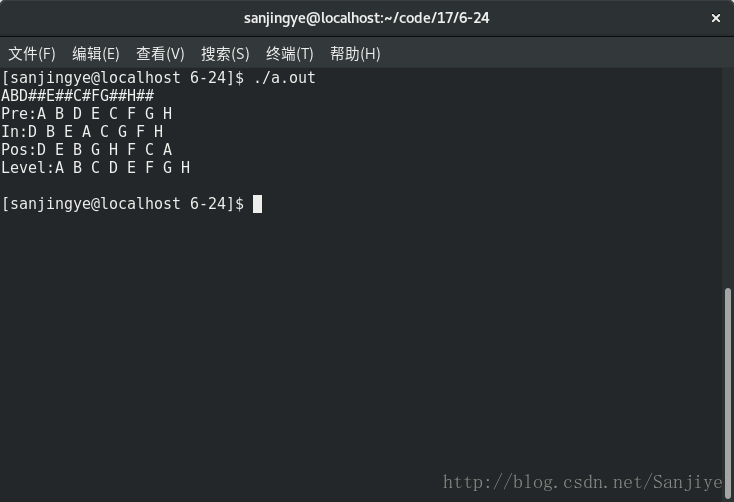
二叉树的层次遍历需要用到队列方面的知识,二叉树之前已经讲过一部分操作,这次主要讲二叉树的层次遍历
用队列实现层次遍历的过程为:首先将根结点入队,然后出队,再将根结点的两个子节点分别入队(默认为先左后右)并判断节点是否为空,为空不进行入队,不为空入队,然后继续进行出队操作,再将出队元素的两个节点入队,只要队列不为空就持续该操作。
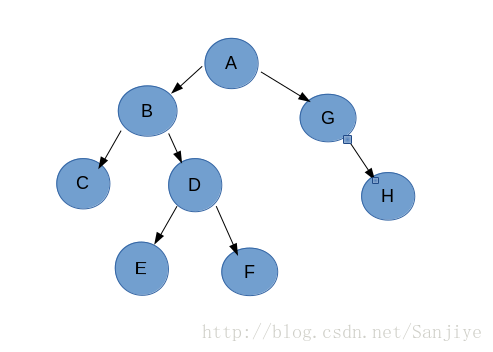
上图层次遍历的结果应当为A B G C D H E F ,下面咱们来看操作
二叉树
头文件
#ifndef _TREE_H
#define _TREE_H
#define ElemType char
typedef struct BinTreeNode //二叉树节点类型
{
ElemType data;
BinTreeNode* leftChild;
BinTreeNode* rightChild;
}BinTreeNode;
typedef struct //二叉树根结点
{
BinTreeNode* root;
ElemType ref;
}BinTree;
void InitBinTree(BinTree *t); //初始化根结点
void CreateBinTree(BinTree* t,const char* &p);
void CreateBinTree(BinTreeNode* &t,const char* &p);
void PreOrder(BinTree* t); //前序遍历
void PreOrder(BinTreeNode* t);
void InOrder(BinTree* t); //中序遍历
void InOrder(BinTreeNode* t);
void PosOrder(BinTree* t); //后序遍历
void PosOrder(BinTreeNode* t);
void LevelOrder(BinTree* t); //层次遍历
void LevelOrder(BinTreeNode* t);
#endif函数的实现
#include<iostream>
using namespace std;
#include<assert.h>
#include"Tree.h"
#include"queue.h"
void InitBinTree(BinTree *t) //初始化根结点
{
t->root=NULL;
t->ref='#';
}
void CreateBinTree(BinTree* t) //创建二叉树
{
CreateBinTree(t->root);
}
void CreateBinTree(BinTreeNode* &t)
{
ElemType item;
cin>>item;
if(item=='#')
{
t=NULL;
}
else
{
t=(BinTreeNode*)malloc(sizeof(BinTreeNode));
assert(t!=NULL);
t->data=item;
CreateBinTree(t->leftChild);
CreateBinTree(t->rightChild);
}
}
void PreOrder(BinTree* t) //前序遍历
{
PreOrder(t->root);
}
void PreOrder(BinTreeNode* t)
{
if(t)
{
cout<<t->data<<" ";
PreOrder(t->leftChild);
PreOrder(t->rightChild);
}
}
void InOrder(BinTree* t) //中序遍历
{
InOrder(t->root);
}
void InOrder(BinTreeNode* t)
{
if(t)
{
InOrder(t->leftChild);
cout<<t->data<<" ";
InOrder(t->rightChild);
}
}
void PosOrder(BinTree* t) //后序遍历
{
PosOrder(t->root);
}
void PosOrder(BinTreeNode* t)
{
if(t)
{
PosOrder(t->leftChild);
PosOrder(t->rightChild);
cout<<t->data<<" ";
}
}
void LevelOrder(BinTree* t) //层次遍历
{
LevelOrder(t->root);
}
void LevelOrder(BinTreeNode* t)
{
if(t) //判断根结点是否为空,不为空进行操作
{
queue q;
init_queue(&q);
BinTreeNode* temp=t;
push(&q,temp);
while(Emptyqueue(&q)!=1) //队列不为空持续出队入队
{
pop(&q);
push(&q,temp->leftChild); //在push函数中已经设置若节点为空,则不入队
push(&q,temp->rightChild);
temp=Getfront(&q);
}
cout<<endl;
}
}队列
头文件
#ifndef QUEUE_H
#define QUEUE_H
#include"Tree.h"
#define ElemTypeB BinTreeNode* //宏定义队列存储对像的类型
typedef struct queue
{
ElemTypeB *base;
int capacity;
int front;
int rear;
}queue;
void init_queue(queue* q); //初始化队列
void push(queue* q,ElemTypeB x); // 入队
void pop(queue* q); //出队
int Emptyqueue(queue* q); //判断队列是否为空,为空返回1,不为空返回0
ElemTypeB Getfront(queue* q); //获取队列队头元素
#endif函数实现
#include<iostream>
using namespace std;
#include"queue.h"
#include"assert.h"
void init_queue(queue* q)
{
q->base=(ElemTypeB*)malloc(sizeof(ElemTypeB)*10);
assert(q->base!=NULL);
q->capacity=10;
q->front=q->rear=0;
}
void push(queue* q,ElemTypeB x)
{
if((q->rear+1)%q->capacity==q->front) //判断队列是否已满
{
cout<<"队列已满,无法入队"<<endl;
return;
}
if(x) //判断入队元素是否为空,不为空入队
{
q->base[q->rear++]=x;
q->rear=q->rear%q->capacity;
}
}
void pop(queue* q)
{
if(q->front==q->rear)
{
cout<<"队列已空"<<endl;
return;
}
cout<<(q->base[q->front++])->data<<" ";
q->front%=q->capacity;
}
int Emptyqueue(queue* q)
{
if(q->front==q->rear)
return 1;
return 0;
}
ElemTypeB Getfront(queue* q)
{
return q->base[q->front];
}主函数
#include<iostream>
using namespace std;
#include"Tree.h"
#include"queue.h"
int main()
{
BinTree T;
InitBinTree(&T);
CreateBinTree(&T);
cout<<"Pre:";
PreOrder(&T);
cout<<endl;
cout<<"In:";
InOrder(&T);
cout<<endl;
cout<<"Pos:";
PosOrder(&T);
cout<<endl;
cout<<"Level:";
LevelOrder(&T);
cout<<endl;
}运行结果
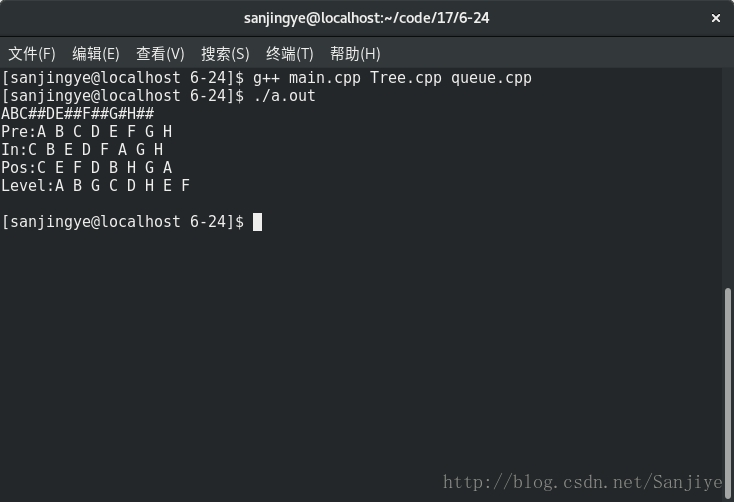
和咱们之前预期的结果一样
再换一组测试数据ABD##E##C#FG##H##
画出对应树形图为
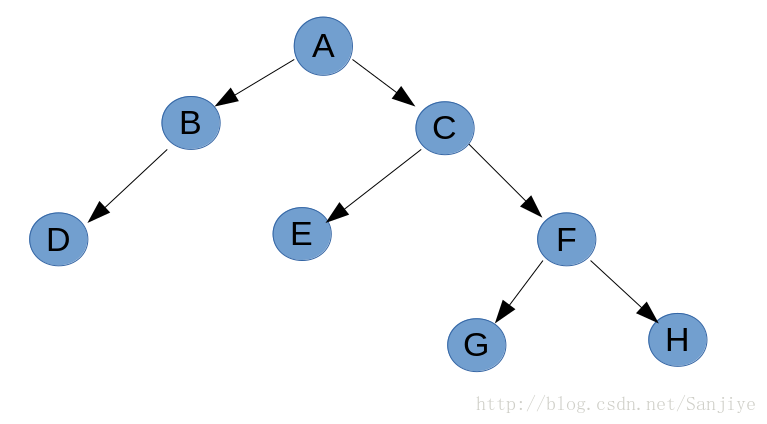
由树形图可以看出层次遍历的结果应当为ABCDEFGH
我们来看运行结果