文章目录

最容易记忆的方式书写,记录所有思路和拓展。分门别类书写。
确定每一个思路的时间复杂度
排序

1.快排(时间复杂度O(nlogn),空间复杂度O(1)),下面的实现是一种原地排序的实现。
class Solution
{
public:
int partition(vector<int> &nums, int l, int r)
{
int k = l, pivot = nums[r];
for (int i = l; i < r; i++)
{
if (nums[i] <= pivot)
std::swap(nums[i], nums[k++]);
}
std::swap(nums[k], nums[r]);
return k;
}
void quick_sort(vector<int> &nums, int l, int r)
{
if (l >= r)
return;
int q = partition(nums, l, r);
quick_sort(nums, l, q - 1);
quick_sort(nums, q + 1, r);
}
vector<int> sortArray(vector<int> &nums)
{
if (nums.size() <= 1)
return nums;
quick_sort(nums, 0, nums.size() - 1);
return nums;
}
};
最差情况是O(n^2),这就在于基准点的选取。
2.堆排
class Solution
{
public:
//构造的是 大顶堆 哦
//每个节点堆化的时间复杂度是:O(logN)
void heapify(vector<int> &a, int n, int i)
{
while (true)
{
int maxPos = i;
if (i * 2 + 1 <= n && a[i] < a[i * 2 + 1]) //左子节点,就是下标为 i∗2+1 的节点,
maxPos = i * 2 + 1;
if (i * 2 + 2 <= n && a[maxPos] < a[i * 2 + 2]) //右子节点,就是下标为 i∗2+2 的节点
maxPos = i * 2 + 2;
if (maxPos == i)
break;
std::swap(a[i], a[maxPos]);
i = maxPos;
}
}
//时间复杂度:O(N)
void buildHeap(vector<int> &nums, int n)
{
//从后向前,非叶子节点是:0 到 n/2-1
for (int i = n / 2 - 1; i >= 0; i--)
{
heapify(nums, n, i);
for (auto tt : nums)
cout << tt << " ";
cout << endl;
}
}
vector<int> sortArray(vector<int> &nums)
{
if (nums.size() <= 0)
return nums;
buildHeap(nums, nums.size() - 1);
int k = nums.size() - 1;
//排序过程的时间复杂度是 O(nlogn)
while (k > 0)
{
//从上到下再 堆化
swap(nums[0], nums[k]); //依此将最大的数字换到数组末尾
--k;
heapify(nums, k, 0);
}
return nums;
}
};
注意:
- 以上下标是从0开始的哦。如果是以1开始的话,那么左子树,右子树下标就不一样了哦!
- 堆排分为两步(建堆O(n)+排序(O(NlogN))),所以总的时间复杂度是O(NlogN)
- 不稳定,空间复杂度是O(1)
3.归并(时间复杂度一直是O(NlogN),空间复杂度O(n))
class Solution
{
public:
void merge_two(vector<int> &nums, int left, int middle, int right, vector<int> &tmp)
{
int k = 0; //临时数组下标
int i = left; //左边数组的起始
int j = middle + 1; //右边数组的起始
while (i <= middle && j <= right)
{
if (nums[i] <= nums[j])
tmp[k++] = nums[i++];
else
tmp[k++] = nums[j++];
}
while (i <= middle)
{
tmp[k++] = nums[i++];
}
while (j <= right)
{
tmp[k++] = nums[j++];
}
std::copy_n(tmp.begin(), k, nums.begin() + left); //拷到原来的地方
}
void merge_sort(vector<int> &nums, int left, int right, vector<int> &tmp)
{
if (left >= right)
return;
int middle = (left + right) >> 1;
merge_sort(nums, left, middle, tmp);
merge_sort(nums, middle + 1, right, tmp);
merge_two(nums, left, middle, right, tmp);
}
vector<int> sortArray(vector<int> &nums)
{
if (nums.size() <= 0)
return nums;
vector<int> tmp(nums.size());
merge_sort(nums, 0, nums.size() - 1, tmp);
return nums;
}
};
4.插入
class Solution
{
public:
void insertSort(vector<int> &nums)
{
for (int i = 1; i < nums.size(); i++)
{
int key = nums[i];
int j = i - 1;
/*查找插入的位置*/
for (; j >= 0; j--)
{
if (nums[j] > key)
nums[j + 1] = nums[j]; /*数据移动*/
else
break;
}
nums[j + 1] = key; //数据插入
}
}
vector<int> sortArray(vector<int> &nums)
{
if (nums.size() <= 1)
return nums;
insertSort(nums);
return nums;
}
};
关于排序延伸的几道题
1.求最小/大的k个数字与求第k小/大的数字
在未排序的数组中找到第 k 个最大的元素。请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
思路:
- 快排的思想。O(n)
- 堆排的思想。 O(NlogK)
快排的思想。O(n)
class Solution
{
public:
int partition(vector<int> &nums, int l, int r)
{
int k = l, privot = nums[r];
for (int i = l; i < r; i++)
{
if (nums[i] >= privot)
std::swap(nums[k++], nums[i]);
}
std::swap(nums[k], nums[r]);
return k;
}
int findKthLargest(vector<int> &vv, int k)
{
int l = 0;
int r = vv.size() - 1;
int q = partition(vv, l, r);
while (q != k-1)
{
if (q > k-1)
{
r = q - 1;
q = partition(vv, l, r);
}
else
{
l = q + 1;
q = partition(vv, l, r);
}
}
return vv[q];
}
};
- 堆排的思想。 O(NlogK)
class Solution
{
public:
int findKthLargest(vector<int> &nums, int k)
{
if (nums.size() <= 0 || nums.size() < k)
return -1;
//最大堆,底层实现的数据结构是 vector ,但需要满足堆的特性
priority_queue<int, std::vector<int>, greater<int>> QQ;
for (int i = 0; i < nums.size(); i++)
{
if (i < k)
{
QQ.push(nums[i]);
}
else if (nums[i] > QQ.top())
{
QQ.pop();
QQ.push(nums[i]);
}
}
return QQ.top();
}
};
2.
查找
二分查找O(logN)
循环实现
class Solution
{
public:
int search(vector<int> &nums, int target)
{
if (nums.size() <= 0)
return -1;
int left = 0;
int right = nums.size() - 1; //right一定要指向最后一个有效的数字
int mid = 0;
while (left <= right)
{
mid = left + ((right - left) >> 1); //这里一定要加括号才行
if (nums[mid] == target)
return mid;
else if (nums[mid] < target)
left = mid + 1;
else
right = mid - 1;
}
return -1;
}
};
递归实现
变异的二分查找
1.旋转数组的最小数字
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。
NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
- 思路:二分的思路就是将其分为两个递增数组,然后看num[mid]属于哪一个数组,最后的结束条件是
low指向第一个递增数组最尾部,high 指向第二个递增数组最头部。注意当有重复元素时,会产生(num[mid]=nums[low] == nums[high])无法判断在那个数组的情况,这时就需要顺序查找了。时间复杂度O(logN)
class Solution
{
public:
int MinFun(vector<int> &nums, int low, int high)
{
int ret = 0;
for (int i = low; i < high - 1; i++)
{
if (nums[i + 1] < nums[i])
{
ret = i + 1;
break;
}
}
return ret;
}
//考虑重复
int minNumberInRotateArray(vector<int> nums)
{
if (nums.size() <= 0)
return 0;
//处理:12345 的特殊情况
if (nums[0] < nums[nums.size() - 1])
return nums[0];
int low = 0;
int high = nums.size() - 1;
int mid = low + ((high - low) >> 1);
//明显的体现出 low指向第一个递增数组最尾部,high 指向第二个递增数组最头部的特点
while (high - low != 1)
{
if (nums[mid] == nums[low] && nums[mid] == nums[high])
{
high = MinFun(nums, low, high);
break;
}
if (nums[mid] >= nums[low])
low = mid;
else if (nums[mid] <= nums[high])
high = mid; //注意这里不能够 +-1,否则会造成死循环
else
break; //54321 的情况
mid = low + ((high - low) >> 1);
}
return nums[high];
}
};
类似题目:https://leetcode-cn.com/problemset/all/?search=%20%E6%97%8B%E8%BD%AC%E6%95%B0%E7%BB%84
2.数字在排序数组中出现的次数
- 思路:
- 1.二分查找到数字,然后左右找。时间复杂度是O(n)
- 2.用两次 二分查找找到第一次出现的位置和最后一次出现的位置,然后下标相减即可。时间复杂度O(logN)
统计一个数字在排序数组中出现的次数。
class Solution
{
public:
//存在返回 对应要求的下标,不存在返回 -1
int GetFristIndex(const vector<int> &data, int k)
{
int low = 0;
int high = data.size() - 1;
int mid = low + ((high - low) >> 1);
while (low <= high)
{
if (data[mid] == k)
{
if (mid == 0 || data[mid - 1] != k)
break;//说明找到了第一次出现的k的位置
else
high = mid - 1;
}
else if (data[mid] < k)
low = mid + 1;
else
high = mid - 1;
mid = low + ((high - low) >> 1);
}
if (low > high)
return -1;
else
return mid;
}
int GetLastIndex(const vector<int> &data, int k)
{
int low = 0;
int high = data.size() - 1;
int mid = low + ((high - low) >> 1);
while (low <= high)
{
if (data[mid] == k)
{
if (mid == data.size() - 1 || data[mid + 1] != k)
break;//说明找到了最后一个k
else
low = mid + 1;
}
else if (data[mid] < k)
low = mid + 1;
else
high = mid - 1;
mid = low + ((high - low) >> 1);
}
if (low > high)
return -1;
else
return mid;
}
int GetNumberOfK(vector<int> data, int k)
{
if (data.size() <= 0)
return 0;
int start = GetFristIndex(data, k);
if (start == -1)
return 0;
int end = GetLastIndex(data, k);
return end - start + 1;
}
};
3.
4.
数组
1. 二维数组中的查找
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
思路:
-
把每一行看成有序递增的数组,
利用二分查找(logN),
通过遍历每一行得到答案,
时间复杂度是nlogn -
利用二维数组由上到下,由左到右递增的规律,那么选取右上角或者左下角的元素与target进行比较。类似于二叉查找树的形式.复杂度是O(logN)
class Solution
{
public:
bool Find(int target, vector<vector<int>> array)
{
//二叉查找树
int row = array.size();
if (row <= 0)
return false;
int col = array[0].size();
for (int j = col - 1, i = 0; j >= 0 && i < row;)
//从右上角开始,注意循环结束条件
{
if (target == array[i][j])
{
return true;
}
else if (target < array[i][j])
{
j--;
}
else
{
i++;
}
}
return false;
}
};
2. 数组中出现次数超过一半的数字
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0。
思路:
- 1.hash_map 辅助,数字作为key。出现的次数作为 value 。时间 O(n),空间 O(n)《略》
- 2.基于Partition 函数的算法。时间O(n),空间O(1)。但会修改输入输入数组!!!
- 3.根据数组特点找出O(n)的算法(数学)。
2.基于 Partition 函数的算法。由于该数字出现的次数超过数组的一半,所以如果我们将数组排序,那么位于最中间的数字就是我们要找的数字啦!也就是说该数字是第n/2大的数字啦。
//方法二
class Solution
{
public:
int partition(vector<int> &vv, int l, int r)
{
int k = l, pivot = vv[r];
for (int i = l; i < r; i++)
{
if (vv[i] <= pivot)
std::swap(vv[k++], vv[i]);
}
std::swap(vv[k], vv[r]);
return k;
}
int MoreThanHalfNum_Solution(vector<int> numbers)
{
int len = numbers.size();
if (len < 1)
return 0;
int left = 0;
int right = len - 1;
int k = partition(numbers, left, right);
while (k != len / 2)
{
if (k < len / 2)
{
left = k + 1;
k = partition(numbers, left, right);
}
else if (k > len / 2)
{
right = k - 1;
k = partition(numbers, left, right);
}
}
int time = 0;
for (auto it : numbers)
{
if (it == numbers[k])
{
time++;
}
}
//数组中出现次数超过一半
if (time > len / 2)
return numbers[k];
else
return 0;
}
};
3.如果有一个数字出现的次数超过了数组的一半,比剩余的其他数字出现的次数的和都要大。因此:
- 我们可以在遍历数组的时候记录两个值:
- 数组中的数字;
- 次数。
- 遍历下一个数字时,若它与之前保存的数字相同,则次数加1,否则次数减1;若次数为0,则保存下一个数字,并将次数置为1。遍历结束后,所保存的数字即为所求。最后再判断它是否符合条件。
class Solution
{
public:
int MoreThanHalfNum_Solution(vector<int> numbers)
{
int len = numbers.size();
if (len < 1)
return 0;
int value = numbers[0];
int count = 1;
for (int i = 1; i < len; i++)
{
if (numbers[i] == value)
count++;
else
count--;
if (count == 0)
{
value = numbers[i];
count = 1;
}
printf("num[%d] == %d ,value == %d ,count == %d \n", i, numbers[i], value, count);
}
//检查找出的这个数是不是出现的次数超过一半
int time = 0;
for (auto it : numbers)
{
if (it == value)
{
time++;
}
}
//数组中出现次数超过一半
if (time > len / 2)
return value;
else
return 0;
}
};
int main()
{
Solution s1;
cout << s1.MoreThanHalfNum_Solution({1, 2, 3, 2, 2, 2, 5, 4, 2}) << endl;
cout << "vffelvnfdknkfnvknfb\n\n\n\n";
cout << s1.MoreThanHalfNum_Solution({1, 2, 3, 2, 4, 2, 5, 2, 3}) << endl;
}

3. 数组中重复的数字
在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的,但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如,如果输入长度为7的数组{2,3,1,0,2,5,3},那么对应的输出是第一个重复的数字2。
思路:
- 排序
- 哈希
- 特殊方法:交换法。题中给出的是一个长度为n的数组,数组的下标是0n-1,数组中的数字也是0n-1。因此,当数组中不存在重复数字且排序之后,数字i将出现在下标为i的位置。由于数组中存在重复数字,因此,按照上面的思路,存在有的位置没有数字,有的位置要存放多个相同的数字。
根据这种思路,我们可以采用交换法解决这个问题。扫描数组,每扫描一个数字,就比较当前数字是否与其下标相等,若相等,继续向后扫描;若不相等,比较以该数字为下标的元素是否与该元素相等,若相等,说明该元素是一个重复元素,向后扫描,否则,交换该元素和数组中以该元素为下标的元素。时间O(n),空间O(1)
class Solution
{
public:
// Parameters:
// numbers: an array of integers
// length: the length of array numbers
// duplication: (Output) the duplicated number in the array number
// Return value: true if the input is valid, and there are some duplications in the array number
// otherwise false
bool duplicate(int numbers[], int length, int *duplication)
{
if (length < 1)
{
return false;
}
for (int i = 0; i < length; i++)
{
if (numbers[i] < 0 || numbers[i] > length - 1)
return false;
}
for (int i = 0; i < length; i++)
{
while (numbers[i] != i)
{
if (numbers[numbers[i]] == numbers[i])
{
*duplication = numbers[i];
return true;
}
else
{
std::swap(numbers[i], numbers[numbers[i]]);
}
}
}
return false;
}
};
4.
字符串
1.替换空格
请实现一个函数,将一个字符串中的每个空格替换成“%20”。例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。
思路:很明显,这样子的替换会改变字符串的大小。所以一种就是使用原来字符串后面的内存,一种就是自己分配内存。
如何替换:
- 从前向后扫描,遇到空格就替换,需要移动元素。时间复杂度O(n^2)
从后往前遍历并替换,一个指针指向新的,一个指向旧的。遍历旧的字符串对新指针直接赋值或者替换即可。时间复杂度O(n)
- 从前向后扫描,遇到空格就替换,需要移动元素。时间复杂度O(n^2)
class Solution {
public:
void replaceSpace(char *str,int length) {
for(int i= 0 ;i< length ;)
{
if(str[i] == ' ')
{
for(int j = length-1 ;j >= i ;j--)
{
str[j+2] = str[j];
}
str[i++]= '%';
str[i++] ='2';
str[i++] ='0';
continue;
}
i++;
}
}
};
从后往前遍历并替换,一个指针指向新的,一个指向旧的。遍历旧的字符串对新指针直接赋值或者替换即可。时间复杂度O(n)
class Solution
{
public:
//length 为str 的 内存capity
void replaceSpace(char *str, int length)
{
if (str == nullptr || length == 0)
return;
int spaceNumber = 0;
int originLength = 0;
//统计空格和str的长度
char *tmp = str;
while (*tmp != '\0')
{
originLength++;
if (*tmp == ' ')
spaceNumber++;
tmp++;
}
int indexOrigin = originLength; //将'\0'也直接当作非空格自负处理即可
int indexNew = originLength + 2 * spaceNumber;
if (indexNew > length)
return;
while (indexOrigin >= 0 && indexNew > indexOrigin)
{
if (str[indexOrigin] != ' ')
{
str[indexNew--] = str[indexOrigin];
}
else
{
str[indexNew--] = '0';
str[indexNew--] = '2';
str[indexNew--] = '%';
}
indexOrigin--;
}
}
};
拓展:合并两个数组(字符串)的时候都可以使用这种方法,会减少移动的次数,提高效率
https://leetcode-cn.com/problems/merge-sorted-array/
2. 书写一个upCase函数
char *upCase(const char *str) //const 属性
{
cout << *str << endl;
char *ret = new char(strlen(str) + 1);
//strlen 开头和终止空字符之间的字符数(不包括终止空字符‘\0’本身).
char *tmp = ret;
while (*str)
{
cout << *str << " ";
if (*str >= 'a' && *str <= 'z')
*tmp = *str - 32;
else
*tmp = *str;
str++;
tmp++;
}
cout << endl;
*tmp = '\0'; //需要调整以满足字符串的格式
return ret;
}
int main()
{
char str[] = "liu shE4ng xi!!!";
cout << str << endl;
cout << upCase(str) << endl;
return 0;
}

3. leetcode151. 翻转字符串里的单词
给定一个字符串,逐个翻转字符串中的每个单词。
示例 1:
输入: “the sky is blue”
输出: “blue is sky the”
示例 2:
输入: " hello world! "
输出: “world! hello”
解释: 输入字符串可以在前面或者后面包含多余的空格,但是反转后的字符不能包括。
示例 3:
输入: “a good example”
输出: “example good a”
解释: 如果两个单词间有多余的空格,将反转后单词间的空格减少到只含一个。
说明:
无空格字符构成一个单词。
输入字符串可以在前面或者后面包含多余的空格,但是反转后的字符不能包括。
如果两个单词间有多余的空格,将反转后单词间的空格减少到只含一个。
进阶:
请选用 C 语言的用户尝试使用 O(1) 额外空间复杂度的原地解法。
链接:https://leetcode-cn.com/problems/reverse-words-in-a-string
注意这道题有很多的坑点需要注意:
- 中间有很多空格
- 前后有空格
- 字符串输入为空,字符串输入只有空格。
思路:
- 1.直接利用 stringstream 提取单词,利用 string 的 + 号逆序添加。(非原地算法)
- 2.上面的算法主要耗时点在逆序插入上。那么我们给他变成顺序插入看看。(非原地算法)
- 3.就是剑指offer上面的做法 。先逆转整个字符串,然后逆转每一个单词。(原地算法)
直接利用 stringstream 提取单词,利用 string 的 + 号(insert也一样)逆序添加。
class Solution
{
public:
string reverseWords(string s)
{
string ans, str;
stringstream ss(s);
ss >> str;
ans.insert(0, str); //特殊处理第一个单词
while (ss >> str)
ans.insert(0, str + " ");//最主要的耗时也在这里 ?❤️?
return ans.size() ? ans : "";
}
};
变成顺序插入看看。(非原地算法)
class Solution
{
public:
string reverseWords(string s)
{
string ans, tmp;
stringstream ss(s);
vector<string> vv;
while (ss >> tmp)
vv.push_back(tmp); //全部流入 vector 容器中
//处理 字符串输入为空,字符串输入只有空格 的情况
if (vv.size() < 1)
return ans;
for (int i = vv.size() - 1; i > 0; i--)
{
ans += vv[i] + " ";
}
//特殊处理 最终放置在 尾部 的单词
ans += vv[0];
return ans.size() ? ans : "";
}
};
//虽然我是这样写的,但是我觉得如下这样写是看起来最简洁明了的代码。上面一个解法也是一样。
class Solution
{
public:
string reverseWords(string s)
{
string ans, tmp;
stringstream ss(s);
vector<string> vv;
while (ss >> tmp)
vv.push_back(tmp); //全部流入 vector 容器中
for (int i = vv.size() - 1; i >= 0; i--)
{
ans += vv[i] + " ";
}
return ans.size() ? string(ans.begin(), ans.end() - 1) : "";
//去掉多加的一个空格
}
};
剑指offer上面的做法 。先逆转整个字符串,然后逆转每一个单词。(原地算法),剑指offer上面的输入中间是没有多个空格的。
class Solution
{
public:
template <typename T> //摘自 std::reverse
void reverseFun(T frist, T last)
{
while ((frist != last) && (frist != --last))
{
std::iter_swap(frist++, last);
}
}
string reverseWords(string s)
{
if (s.size() <= 0)
return s;
reverseFun(s.begin(), s.end()); //翻转整体
int start = 0, end = s.size() - 1;
while (s[start] == ' ' && start <= end)
start++;
while (s[end] == ' ' && end >= start)
end--;
if (start > end)
{
return s; //特殊情况即字符串全为空字符
}
// 翻转中间的单词
for (int i = start; i <= end; i++)
{
while (s[i] == ' ' && i <= end)
{
i++;
}
int l = i;
while (s[i] != ' ' && i <= end)
{
i++;
}
reverseFun(s.begin() + l, s.begin() + i);
}
// 处理中间部分多 ? 的空格
int tail = start;
for (int i = start; i <= end; i++)
{
if (s[i] == ' ' && s[i + 1] == ' ')
{
continue;
}
s[tail++] = s[i];
}
return s.substr(start, tail - start);
}
};
4.左旋转字符串
对于一个给定的字符序列S,请你把其循环左移K位后的序列输出。例如,字符序列S=”abcXYZdef”,要求输出循环左移3位后的结果,即“XYZdefabc”。是不是很简单?OK,搞定它!
这个思路还用说吗?
class Solution
{
public:
string LeftRotateString(string str, int n)
{
if(str.size()<= 0)
return string();
if(n == 0)
return str;
string tt = str.substr(0, n );
string rr = str.substr(n, str.size());
return rr + tt;
}
};
emmmm,将abcXYZdef分为abc和其他。分别将他们翻转。得到cba fedZYX。然后再整体翻转得到 XYZdefabc,即为最终所求结果!!!时间O(n),空间O(1)
class Solution
{
public:
template <typename T> //摘自 std::reverse
void reverseFun(T frist, T last)
{
while ((frist != last) && (frist != --last))
{
std::iter_swap(frist++, last);
}
}
string LeftRotateString(string str, int n)
{
if (str.size() <= 0)
return str;
if (n == 0)
return str;
reverseFun(str.begin(), str.begin() + n);
reverseFun(str.begin() + n, str.end());
reverseFun(str.begin(), str.end());
return str;
}
};
5.字符串转换整数
https://leetcode-cn.com/problems/string-to-integer-atoi/
请你来实现一个 atoi 函数,使其能将字符串转换成整数。
首先,该函数会根据需要丢弃无用的开头空格字符,直到寻找到第一个非空格的字符为止。
当我们寻找到的第一个非空字符为正或者负号时,则将该符号与之后面尽可能多的连续数字组合起来,作为该整数的正负号;假如第一个非空字符是数字,则直接将其与之后连续的数字字符组合起来,形成整数。
该字符串除了有效的整数部分之后也可能会存在多余的字符,这些字符可以被忽略,它们对于函数不应该造成影响。
注意:假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时,则你的函数不需要进行转换。
在任何情况下,若函数不能进行有效的转换时,请返回 0。
说明:
假设我们的环境只能存储 32 位大小的有符号整数,那么其数值范围为 [−231, 231 − 1]。如果数值超过这个范围,请返回 INT_MAX (231 − 1) 或 INT_MIN (−231) 。
示例 1:
输入: “42”
输出: 42
示例 2:
输入: " -42"
输出: -42
解释: 第一个非空白字符为 ‘-’, 它是一个负号。
我们尽可能将负号与后面所有连续出现的数字组合起来,最后得到 -42 。
示例 3:
输入: “4193 with words”
输出: 4193
解释: 转换截止于数字 ‘3’ ,因为它的下一个字符不为数字。
示例 4:
输入: “words and 987”
输出: 0
解释: 第一个非空字符是 ‘w’, 但它不是数字或正、负号。
因此无法执行有效的转换。
示例 5:
输入: “-91283472332”
输出: -2147483648
解释: 数字 “-91283472332” 超过 32 位有符号整数范围。
因此返回 INT_MIN (−231) 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/string-to-integer-atoi
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路:
class Solution
{
public:
int myAtoi(string str)
{
double result = 0;
int tag = 1;
int frist = 0;
while (str[frist] == ' ')
frist++;
switch (str[frist])
{
case '-':
frist++;
tag = -1;
break;
case '+':
frist++;
break;
}
for (int i = frist; i < str.size(); i++)
{
if (str[i] <= '9' && str[i] >= '0')
result = result * 10 + (str[i] - '0');
else
break;
}
result *= tag;
if (result > INT_MAX)
return INT_MAX;
else if (result < INT_MIN)
return INT_MIN;
else
return result;
}
};
链表
1.链表的逆置
当打算修改输入的数据时,最好问清面试官是否可以!!!
思路:
- 使用栈的结构,时间复杂度O(n),空间复杂度O(n)
- 递归,时间复杂度O(n),空间复杂度O(n),由于使用递归,将会使用隐式栈空间。递归深度可能会达到 n 层。
- 修改输入数据,逆置链表,时间复杂度O(n),空间复杂度O(1)
- 使用栈的结构
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) :
* val(x), next(NULL) {
* }
* };
*/
class Solution
{
public:
vector<int> printListFromTailToHead(ListNode *head)
{
vector<int> res;
std::stack<ListNode *> QQ;
ListNode *p = head;
while (p)
{
QQ.push(p);
p = p->next;
}
while (!QQ.empty())
{
res.push_back(QQ.top()->val);
QQ.pop();
}
return res;
}
};
- 递归的方式
class Solution {
public:
ListNode* reverseList(ListNode* head) {
// 0 node || at the end of list
if (head == nullptr || head->next == nullptr) {
return head;
}
ListNode* HEAD = reverseList(head->next);
head->next->next = head;
head->next = NULL;
return HEAD;
}
};
- 迭代的方式(头插法嘛)
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution
{
public:
ListNode *reverseList(ListNode *head)
{
if (head == nullptr)
return nullptr;
ListNode *prev = nullptr;
ListNode *curr = head;
ListNode *nextTemp = nullptr;
while (curr)
{
nextTemp = curr->next;
curr->next = prev;
prev = curr;
curr = nextTemp;
}
return prev;
}
};
2.在O(1)时间内删除链表节点
请编写一个函数,使其可以删除某个链表中给定的(非末尾)节点,你将只被给定要求被删除的节点。
输入: head = [4,5,1,9], node = 5
输出: [4,1,9]
解释: 给定你链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9.
思路:OK。我们现在知道了需要删除的节点。那么我们把后面节点的内容覆盖到前面需要删除的节点,然后把后面的节点删除掉就行了呗。
时间复杂度O(1)
注意有几大坑点:
- 只有一个节点,删除节点位于头节点(也是尾节点)
- 删除节点位于尾节点
- 需要调用者确保要删除的节点在该链表中。
void DeleteNode(ListNode *head, ListNode *deListNode)
{
if (deListNode == nullptr || head == nullptr)
return;
//1.普通情况
if (deListNode->next)
{
ListNode *p = deListNode->next;
deListNode->val = deListNode->next->val;
deListNode->next = deListNode->next->next;
delete p;
p = nullptr;
}
//2.只有一个节点
else if (head == deListNode)
{
delete deListNode;
deListNode = nullptr;
head = nullptr;
}
//3.删除的节点是尾节点
else
{
ListNode *p = head;
while (p->next != deListNode)
{
p = p->next;
}
p->next = nullptr;
delete deListNode;
deListNode = nullptr;
}
}
3.链表中的倒数第k个节点
输入一个链表,输出该链表中倒数第k个结点。
思路:双指针思路。时间复杂度 O(n)
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};*/
class Solution
{
public:
ListNode *FindKthToTail(ListNode *head, unsigned int k)
{
if (head == nullptr || k == 0)
return nullptr;
ListNode *p1 = head;
ListNode *p2 = head;
for (int i = 0; i < k-1 ; i++) //注意 k-1
{
if (p2->next)
p2 = p2->next;
else //如果 k 比链表整个的长度还要长,怎么办?
return nullptr;
}
while (p2->next)//不需要循环到 nullptr
{
p1 = p1->next;
p2 = p2->next;
}
return p1;
}
};
拓展:找最中间的节点和判断是否成环也是双指针的思路
4.合并两个排序的链表
5.两个链表的第一个公共节点
6.环形链表(圆圈中最后剩下的数字)
- 约瑟夫环的问题。时间复杂度O(MN),空间复杂度O(N)
class Solution
{
public:
int LastRemaining_Solution(int n, int m)
{
if (n < 1 || m < 1)
return -1;
std::list<int> ll;
for (int i = 0; i < n; i++)
ll.push_back(i);
auto it = ll.begin();
while (ll.size() != 1)
{
for (int i = 0; i < m - 1; i++)
{
it++;
if (it == ll.end())
it = ll.begin();
}
//删除 第 m 个
auto tmp = it;
it++;
if (it == ll.end())
it = ll.begin();
ll.erase(tmp);
}
return *it;
}
};
- 经过上面复杂的分析,我们终于找到了一个递归公式。
要得到n个数字的序列中最后剩下的数字,只需要得到n-1个数字的序列中最后剩下的数字,并以此类推。当n=1时,也就是序列中开始只有-一个数字0,那么很显然最后剩下的数字就是0。我们把这种关系表示为:
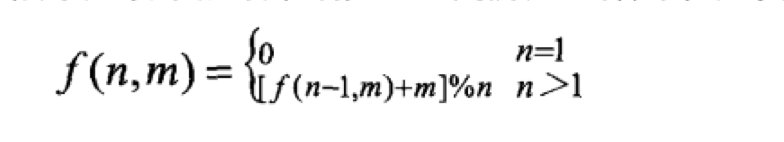
时间复杂度O(n),空间复杂度O(1)
class Solution
{
public:
int LastRemaining_Solution(int n, int m)
{
if (n < 1 || m < 1)
return -1;
int last = 0;
for (int i = 2; i <= n; i++)
last = (last + m) % i;
return last;
}
};
7.二叉搜索树与双向链表
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
思路:

时间复杂度O (n)
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution {
public:
//左 根 右
TreeNode *lastMax = nullptr ;
void ConvertNode(TreeNode* node){
if(node)
{
if(node->left)
ConvertNode(node->left);
node->left = lastMax;
if(lastMax)
lastMax->right = node;
lastMax = node ;
if(node->right)
ConvertNode(node->right);
}
}
TreeNode* Convert(TreeNode* root)
{
if(root == nullptr )
return nullptr;
//先找到需要返回的节点的指针
TreeNode *ret = root;
while(ret->left)
ret = ret->left;
ConvertNode(root);
return ret;
}
};
8.复杂链表的复制
给定一个链表,每个节点包含一个额外增加的随机指针,该指针可以指向链表中的任何节点或空节点。
要求返回这个链表的深拷贝。
class Solution
{
public:
//1.复制节点
void CloneNodes(Node *pHead)
{
Node *p = pHead;
while (p)
{
Node *pNew = new Node(p->val, nullptr, nullptr);//一定要置空,不然过不了
pNew->next = p->next; //节点的中间插入法
p->next = pNew;
p = pNew->next;
}
}
//2.设置 random 指针
void SetRandom(Node *pHead)
{
Node *p = pHead;
Node *pClone = nullptr;
while (p)
{
pClone = p->next;
if (p->random)
{
pClone->random = p->random->next;
}
p = pClone->next;
}
}
//3.将复制链表从原链表分离。
Node *GetResult(Node *head)
{
Node *node = head;
Node *newHead = head->next;
Node *newNode = head->next;
while (node != nullptr)
{
node->next = node->next->next;
if (newNode->next != nullptr)
{
newNode->next = newNode->next->next;
}
node = node->next;
newNode = newNode->next;
}
return newHead;
}
Node *copyRandomList(Node *pHead)
{
if (pHead == nullptr)
return nullptr;
CloneNodes(pHead);
SetRandom(pHead);
return GetResult(pHead);
}
};
树
0.树三种递归&&非递归遍历&&层次遍历
1.重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
思路:
前序遍历序列的第一个节点是根节点,可以根据根节点将中序遍历序列划分成左子树区间和右子树区间。根据左子树和右子树节点的个数,又可以将前序遍历序列划分成左子树区间和右子树区间。因此得到了左子树的前序遍历序列和中序遍历序列、右子树的前序遍历序列和中序遍历序列。递归构造左右子树
class Solution
{
public:
TreeNode *buildTree(vector<int> &pre, vector<int> &vin)
{
if (pre.empty() || vin.empty() || (pre.size() != vin.size()))
{
return nullptr;
}
return reConstructBinaryTreeCore(pre, 0, pre.size() - 1, vin, 0, vin.size() - 1);
}
TreeNode *reConstructBinaryTreeCore(const vector<int> &pre, int preL, int preR,
const vector<int> &vin, int vinL, int vinR)
{
if (preL > preR)
return nullptr;
TreeNode *root = new TreeNode(pre.at(preL));
int i = vinL;
for (; i <= vinR; i++)
{
if (vin.at(i) == pre.at(preL))
break;
}
int leftsz = i - vinL;
int rightsz = vinR - i;
root->left = reConstructBinaryTreeCore(pre, preL + 1, preL + leftsz,
vin, vinL, i - 1);
root->right = reConstructBinaryTreeCore(pre, preL + leftsz + 1, preR,
vin, i + 1, vinR);
return root;
}
};
2.二叉树的深度
输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。时间复杂度为O(N),空间复杂度为O(logN)。
思路:
- 如果没有左右子树,深度为1
如果只有左子树,深度为左子树深度加1
如果只有右子树,深度为右子树深度加1
如果都有,深度为左子树和右子树深度较大者加1
class Solution {
public:
int TreeDepth(TreeNode* pRoot)
{
if(!pRoot)
return 0;
int left = TreeDepth(pRoot->left);
int right = TreeDepth(pRoot->right);
return (left > right)? left+1 : right+1;
}
};
2.1 平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:
给定二叉树 [3,9,20,null,null,15,7]
3
/
9 20
/
15 7
返回 true 。
示例 2:
给定二叉树 [1,2,2,3,3,null,null,4,4]
1
/ \
2 2
/ \
3 3
/
4 4
返回 false 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/balanced-binary-tree
思路:
- 1.对每一个节点分别求左右子树的高度,然后通过遍历所有节点得到答案。这样会重复遍历树的节点。让我想起了美团出的那道面试题,难怪人家会问我还有更好的解决方案吗??
class Solution
{
public:
int getDeep(TreeNode *root)
{
if (!root)
return 0;
int ll = getDeep(root->left);
int rr = getDeep(root->right);
return ll > rr ? ll + 1 : rr + 1;
}
bool isBalanced(TreeNode *root)
{
if (root)
{
int ll = getDeep(root->left);
int rr = getDeep(root->right);
if (std::abs(ll - rr) > 1)
{
return false;
}
return isBalanced(root->left) && isBalanced(root->right);
}
return true;
}
};
- 2.在求高度的过程中判断是否是平衡二叉树。这样子每个节点只遍历一遍的解法,才是面试官想要的东西。
class Solution
{
public:
int getDeep(TreeNode *root)
{
if (!root)
return 0;
int ll = getDeep(root->left);
if (ll == -1)
return -1;
int rr = getDeep(root->right);
if (rr == -1)
return -1;
//这里就已经是递归计算高度了,直接使用一下
if (std::abs(ll - rr) > 1)
{
return -1;
}
else
{
return 1 + std::max(ll, rr);
}
}
bool isBalanced(TreeNode *root)
{
if (getDeep(root) == -1)
return false;
else
return true;
}
};
3.树的子结构
输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们约定空树不是任意一个树的子结构)
思路:
- 先判断当前以及对应的左右子树,这是比较完整的一颗树的流程。
然后 如果当前的就不满足要求的话,就看左子树与其的对比。右子树也相同。
class Solution
{
public:
bool HasSubtree(TreeNode *s, TreeNode *t)
{
if (s == nullptr || t == nullptr)
return false;
bool ret = false;
//完整的判断是否相同
if (t->val == s->val)
{
//判断左右子树
ret = sameTree(s->left, t->left) && sameTree(s->right, t->right);
if (ret)
return true;
}
return (HasSubtree(s->left, t) || HasSubtree(s->right, t));
}
bool sameTree(TreeNode *p1, TreeNode *p2)
{
if (p2 == nullptr)
return true;
if (p1 == nullptr)
return false;
if (p1->val == p2->val)
return sameTree(p1->left, p2->left) && sameTree(p1->right, p2->right);
else
return false;
}
};
4.二叉树中和为某一值的路径
输入一颗二叉树的根节点和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
思路:
当用前序遍历的方式访问到某一节点时,把该节点添加到路径(vector)上,并累加该节点的值
- 如果节点为叶节点,并且路径中节点值的和刚好等于输入的整数,则当前路径符合要求,打印出来
- 如果不是叶节点,继续访问子节点
当前节点访问结束后,递归函数将自动回到它的父节点。因此,在函数退出之前要在路径上删除当前节点并减去当前节点的值,以确保返回父节点时路径刚好是从根节点到父节点
class Solution
{
public:
vector<vector<int>> res;
void fun(TreeNode *root, int expectNumber, int curSum, vector<int> &path)
{
curSum += root->val;
path.push_back(root->val);
bool isLeaf = (root->left == nullptr) && (root->right == nullptr);
if (isLeaf && curSum == expectNumber)
res.push_back(path);
if (root->left)
fun(root->left, expectNumber, curSum, path);
if (root->right)
fun(root->right, expectNumber, curSum, path);
path.pop_back();
curSum -= root->val;
}
vector<vector<int>> FindPath(TreeNode *root, int expectNumber)
{
if (root == nullptr)
return res;
vector<int> path;
fun(root, expectNumber, 0, path);
return res;
}
};
5.二叉树的后序遍历序列
6.从上到下遍历二叉树
8.树中两个节点的最近公共祖先 lowest-common-ancestor问题
(1) 树是二叉搜索树
思路就是如果两个节点都比当前的节点大,那么最近公共祖先一定在右子树。
如果两个节点都比当前的节点小,那么最近公共祖先一定在左子树。
否则当前节点就是所需要的节点。
时间O(n),空间O(n)
class Solution
{
public:
TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q)
{
if (!root || !p || !q)
return nullptr;
if (root->val > std::max(p->val, q->val))
return lowestCommonAncestor(root->left, p, q);
else if (root->val < std::min(p->val, q->val))
return lowestCommonAncestor(root->right, p, q);
else
return root;
}
};
(2) 树是普通的二叉树
思路 1:
- 在左、右子树中分别查找是否包含p或q:
- 如果以下两种情况(左子树包含p,右子树包含q/左子树包含q,右子树包含p),那么此时的根节点就是最近公共祖先
- 如果左子树包含p和q,那么到root->left中继续查找,最近公共祖先在左子树里面
- 如果右子树包含p和q,那么到root->right中继续查找,最近公共祖先在右子树里面
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(!root || p == root || q == root )
return root ;
TreeNode* left_lca = lowestCommonAncestor(root->left,p,q);
TreeNode* right_lca = lowestCommonAncestor(root->right,p,q);
if(left_lca && right_lca )
return root;
return left_lca ? left_lca : right_lca;
}
};
思路 2:(适用于普遍的树,不只是二叉树)
用两个容器 ,保存从根节点到输入的两个节点的路径,然后把问题转换成求两个链表的最后最后公共节点。时间复杂度O(logn) ,空间复杂度O(logn)
class Solution
{
vector<vector<TreeNode *>> paths;
vector<TreeNode *> path;
public:
TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q)
{
if (!root || !p || !q)
return nullptr;
if (p == q)
return p;
dfs(root, p, q); //dfs 找到两条路径
// 去找最后相同的一个数字即可
if (paths.size() != 2)
return nullptr;
int idx = 0;
while (idx < paths[0].size() && idx < paths[1].size() && paths[0][idx]->val == paths[1][idx]->val)
{
idx++;
}
return paths[0][idx - 1];
}
private:
void dfs(TreeNode *root, TreeNode *p, TreeNode *q)
{
if (!root)
return;
path.push_back(root);
if (root == p || root == q)
paths.push_back(path);
if (root->left)
dfs(root->left, p, q);
if (root->right)
dfs(root->right, p, q);
path.pop_back();
}
};
(3) 树的节点中存在指向父节点的指针
思路:通过所给的节点去逆着将每个节点串联起来,直到到达根节点。然后就是找两个链表的公共节点的问题。时间复杂度O(n)。空间复杂度O(n)
9.二叉树的镜像与对称的问题
(1) 二叉树的镜像
操作给定的二叉树,将其变换为源二叉树的镜像。
class Solution {
public:
void Mirror(TreeNode *pRoot) {
if(pRoot)
{
std::swap(pRoot->left,pRoot->right);
Mirror(pRoot->left);
Mirror(pRoot->right);
}
}
};
(2)对称的二叉树
请实现一个函数,用来判断一颗二叉树是不是对称的。注意,如果一个二叉树同此二叉树的镜像是同样的,定义其为对称的。
递归:
class Solution
{
public:
bool isSymmetricCore(TreeNode *root1, TreeNode *root2)
{
if (!root1 && !root2)
return true;
if (!root1 || !root2)
return false;
if (root1->val != root2->val)
return false;
return isSymmetricCore(root1->left, root2->right) &&
isSymmetricCore(root1->right, root2->left);
}
bool isSymmetric(TreeNode *root)
{
return isSymmetricCore(root, root);
}
};
迭代:二叉树的层次遍历,然后就是判断是不是回文数组!!!
class Solution
{
public:
bool isSymmetric(TreeNode *root)
{
if (!root)
return true;
std::queue<TreeNode *> QQ;
QQ.push(root);
while (!QQ.empty())
{
int len = QQ.size();
vector<int> vv;
for (int i = 0; i < len; i++)
{
TreeNode *tmp = QQ.front();
QQ.pop();
if (!tmp)
{
vv.push_back(-100);//特殊值,独一无二的值
}
else
{
vv.push_back(tmp->val);
QQ.push(tmp->left);
//这里就会将空指针也给 push 进去,在这道题中是需要这样做的。
QQ.push(tmp->right);
}
}
//判断是不是回文数组
for (int j = 0; j < vv.size() / 2; j++)
{
if (vv[j] != vv[vv.size() - 1 - j])
return false;
}
}
return true;
}
};
(3)
9.二叉搜索树与双向链表
10.求最小的k个数字与求第k小的数字的问题
栈和队列
1.栈的压入、弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。(注意:这两个序列的长度是相等的)
思路:
- 将 pushed 队列中的每个数都 push 到栈中,同时检查这个数是不是 popped 序列中下一个要 pop 的值,如果是就把它 pop 出来。
最后,检查不是所有的该 pop 出来的值都是 pop 出来了。时间复杂度O(n),空间复杂度O(n)
class Solution {
public:
bool validateStackSequences(vector<int>& pushV, vector<int>& popV) {
if (pushV.empty() || popV.empty() || pushV.size() != popV.size())
return true;
std::stack<int> QQ;
int index = 0;
// 遍历的是 push 序列
for (const auto &it : pushV)
{
QQ.push(it);
//栈不空 数组下标不越界 (如果不相等就继续把 push 序列的数字压入栈中)
while (!QQ.empty() && index < pushV.size() && QQ.top() == popV[index])
{
QQ.pop();
index++;
}
}
return index == pushV.size();
}
};
位运算
动态规划和贪心
1.最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
链接:https://leetcode-cn.com/problems/maximum-subarray
思路:
- 贪心 。
如果之前的数值状态不会对我们当前的数值产生减幅,就将其加入进来。时间复杂度O(n),空间复杂度O(1)
class Solution
{
public:
int maxSubArray(vector<int> &nums)
{
int before = 0;
int result = nums[0];
//贪心法 O(n) 的解法
for (int i = 0; i < nums.size(); i++)
{
if (before > 0) //注意判断的是 before
before += nums[i];
else
before = nums[i];
if (before > result) result = before;
}
return result;
}
};
- DP ,dp数组表示以 i 为右端点的最大子序和。时间复杂度O(n),空间复杂度O(n)
class Solution
{
public:
int maxSubArray(vector<int> &vv)
{
if (vv.size() <= 0)
return -1;
vector<int> dp(vv.size());
int res = vv[0];
dp[0] = vv[0];
for (int i = 1; i < vv.size(); i++)
{
dp[i] = std::max(vv[i], vv[i] + dp[i - 1]); //DP 方程
if (res < dp[i])
res = dp[i];
}
return res;
}
};
- 分治法 时间O(nlogn),空间O(1)
2.剪绳子/切割杆的问题
给你一根长度为n的绳子,请把绳子剪成m段(m、n都是整数,n>1并且m>1),每段绳子的长度记为k[0],k[1],…,k[m]。请问k[0]xk[1]x…xk[m]可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
思路:
- 贪心 / 动态规划
动态规划:
设f(n)代表长度为n的绳子剪成若干段的最大乘积,如果第一刀下去,第一段长度是i,那么剩下的就需要剪n-i,那么 f(n)=max{f(i)*f(n-i)}。而f(n)的最优解对应着f(i)和f(n-i)的最优解,假如f(i)不是最优解,那么其最优解和f(n-i)乘积肯定大于f(n)的最优解,和f(n)达到最优解矛盾,所以f(n)的最优解对应着f(i)和f(n-i)的最优解。
首先,剪绳子是最优解问题,其次,大问题包含小问题,并且大问题的最优解包含着小问题的最优解,所以可以使用动态规划求解问题,并且从小到大求解,把小问题的最优解记录在数组中,求大问题最优解时就可以直接获取,避免重复计算。
n<2时,由于每次至少减一次,所以返回0。n=2时,只能剪成两个1,那么返回1。n=3时,可以剪成3个1,或者1和2,那么最大乘积是2。当n>3时,就可以使用公式进行求解。
f(4)=max{f(1)f(3), f(2)f(2)}
f(5)=max{f(1)f(4), f(2)f(3)}`
...
f(n)=max{f(1)f(n-1), f(2)f(n-2), f(3)f(n-3), ..., f(i)(fn-i), ...}
class Solution
{
public:
int cutRope(int n)
{
if (n < 2)
return 0;
if (n == 2)
return 1;
if (n == 3)
return 2;
vector<int> dp(n + 1, 0);
//数组中第i个元素表示 把长度为i的绳子剪成 若干段之后 各段长度乘积的最大值
dp[1] = 0;
dp[1] = 1;
dp[2] = 2;
dp[3] = 3;
for (int i = 4; i <= n; i++)
{
int Max = 0;
for (int j = 1; j <= i / 2; j++)
{
int product = dp[j] * dp[i - j];
if (product > Max)
Max = product;
}
dp[i] = Max;
}
return dp[n];
}
};
贪心:(需要一定的数学知识,暂时略)
3.动态规划:字符串编辑距离(edit distance)
Posted on 2017-05-21 | In 动态规划
转载请注明出处:blog.justkitt.com
问题描述
有两个字符串A和B,现在将A经过三种变换可以得到B,即插入、删除和修改,这三种操作的代价分别为c0,c1和c2,问题就是A到B的变换所需要的最小代价是多少。
思路
典型的动态规划问题,娇哥曾经说过,字符串的问题大部分都是动态规划的问题,那么这个问题要怎么解决呢?动态规划问题首先定义状态,然后定义状态转移方程,然后确定初始状态和终止状态,然后就可以得到终止状态下的结果输出。
定义状态
我们定义状态dp[i][j]表示A从0-i和B从0-j这两段的最小编辑距离。状态的定义需要注意的是,状态只能和前面的情况有联系不能和后面的情况有联系。
转移方程
有了状态,那么就定义状态转移方程,状态转移方程的定义有时候会需要“找规律”,但是这道题的规律比较明显,很容易知道,当A[i] == B[j]的时候,从dp[i-1][j-1]到dp[i][j]是不需要任何编辑的,所以dp[i-1][j-1] = dp[i][j],但是当他们不相等的时候,就需要考虑是插入、删除还是编辑的代价最短了,那么自然而然地有三种情况:插入,删除和编辑。插入的情况是什么?
插入是A在和B的前j-1个比,然后再在A的基础上进行插入一个字符,插入的字符是B的第j位,所以插入的代价是dp[i][j-1]+c0
删除是A的前i-1个和B的j个比,因为把A删除了一个字符,所以删除的代价是dp[i-1][j]+c1
编辑是A的前i-1个和B的j-1个比,然后把A的第i位变成B的第j位。所以编辑的代价是dp[i-1][j-1]+c2
由以上分析,可以得到状态转移方程如下:

有了状态转移方程,代码就很好写了。代码如下
int findMinCost(string A, int n, string B, int m, int c0, int c1, int c2) {
vector<vector<int>> dp(n+1,vector<int>(m+1,0));
for(int i = 1;i<=m;++i){
dp[0][i] = dp[0][i-1]+c0;
}
for(int i = 1;i<=n;++i){
dp[i][0] = dp[i-1][0] + c1;
}
for(int i = 1;i<=n;++i){
for(int j = 1;j<=m;++j){
if(A[i-1] == B[j-1])
dp[i][j] = dp[i-1][j-1];
else
dp[i][j] = min(min(dp[i-1][j]+c1,dp[i-1][j-1]+c2),
dp[i][j-1]+c0);
}
}
return dp[n][m];
回溯法和DFS,BFS
1.矩阵中的路径/单词搜索
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。 例如 a b c e s f c s a d e e 矩阵中包含一条字符串"bcced"的路径,但是矩阵中不包含"abcb"路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入该格子。

思路:DFS
class Solution
{
private:
int dir[4][2] = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
int row = 0;
int col = 0;
public:
bool check(vector<vector<char>> &board,
const string &word, const int pathLength, int rr, int cc)
{
if (rr < 0 || rr > row - 1)
return false;
if (cc < 0 || cc > col - 1)
return false;
if (board[rr][cc] != word[pathLength])
return false;
return true;
}
bool dfs(vector<vector<char>> &board, const string &word,
int pathLength, int r, int c, vector<vector<int>> &visted)
{
if (pathLength == word.size())
return true;
for (int i = 0; i < 4; i++)
{
int rr = r + dir[i][0];
int cc = c + dir[i][1];
if (check(board, word, pathLength, rr, cc) && visted[rr][cc] != 1)
{
visted[rr][cc] = 1;
if (dfs(board, word, pathLength + 1, rr, cc, visted)) //注意这里的 pathLength + 1
return true;
visted[rr][cc] = 0;
}
}
return false;
}
bool exist(vector<vector<char>> &board, string word)
{
if (word == "")
return true;
if (board.empty())
return false;
row = board.size();
col = board[0].size();
vector<vector<int>> visted(row, vector<int>(col, 0));
int pathLength = 0;
for (int i = 0; i < row; i++)
{
for (int j = 0; j < col; j++)
{
if (visted[i][j] != 1 && board[i][j] == word[0])
{
visted[i][j] = 1;
if (dfs(board, word, pathLength + 1, i, j, visted))
return true;
visted[i][j] = 0;
}
}
}
return false;
}
};
简单优化就是直接将 board 修改掉来表示是否走过 ,不实用辅助空间visted,从而降低空间复杂度。
2.子集
/给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]/
class Solution
{
public:
vector<vector<int>> subsets(vector<int> &nums)
{
result.push_back(path);
dfs(0, nums);
return result;
}
private:
vector<vector<int>> result;
vector<int> path;
void dfs(int index, const vector<int> &nums)
{
for (int i = index; i < nums.size(); i++)
{
path.push_back(nums[i]);
result.push_back(path);
//便于理解
for(auto i:path)
cout << i<<" ";
cout << endl;
dfs(i+1, nums);
path.pop_back();
}
}
};

3.
k 数之和的问题
1.两数之和
思路:
- 哈希表维护 数值到下标的映射。时间O(n),空间O(n)
class Solution
{
public:
vector<int> twoSum(vector<int> &nums, int target)
{
unordered_map<int, int> map;
vector<int> res;
for (int i = 0; i < nums.size(); i++)
{
if (map.find(target - nums[i]) != map.end())
{
res.push_back(map[target - nums[i]]);
res.push_back(i);
return res;
}
map[nums[i]] = i;
}
return res;
}
};
2.两数之和 II - 输入有序数组
给定一个已按照升序排列 的有序数组,找到两个数使得它们相加之和等于目标数。
函数应该返回这两个下标值 index1 和 index2,其中 index1 必须小于 index2。
说明:
返回的下标值(index1 和 index2)不是从零开始的。
你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/two-sum-ii-input-array-is-sorted
思路:
- 双指针思想,时间复杂度O(n),空间复杂度O(1)
class Solution
{
public:
vector<int> twoSum(vector<int> &numbers, int target)
{
if (numbers.size() < 2)
return {};
int start = 0, end = numbers.size() - 1;
while (start < end)
{
int addUp = numbers[start] + numbers[end];
if (addUp > target)
end--;
else if (addUp < target)
start++;
else
return {start + 1, end + 1};
}
return {};
}
};
3.两数之和 IV - 输入 BST
给定一个二叉搜索树和一个目标结果,如果 BST 中存在两个元素且它们的和等于给定的目标结果,则返回 true。
案例 1:
输入:
5
/
3 6
/ \
2 4 7
Target = 9
输出: True
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/two-sum-iv-input-is-a-bst
思路:
- 1.HashSet 法
任意方法遍历,通过把遍历的值记录到 set 中,然后在遍历的过程中通过 set.contains(target - node.val) 来判断是否存在。
时间复杂度 O(N),空间复杂度 O(N)
- 2.双指针法
通过中序遍历可以把值存入一个 list 中,而且该 list 中的值升序排列。我们可以用两个指针分别指向头和尾,然后通过判断他们的和与 target 的大小关系来移动头指针或者尾指针,最终得出结果。
时间复杂度 O(N),空间复杂度 O(N)
- 3.BST 查找法
时间复杂度 O(NlogN),空间复杂度 O(1)
class Solution
{
public:
TreeNode *findNum(TreeNode *root, int num)
{
if (root == nullptr)
return nullptr;
if (root->val == num)
return root;
else if (root->val > num)
return findNum(root->left, num);
else
return findNum(root->right, num);
}
bool fun(TreeNode *node, TreeNode *root, int k) // O(n)
{
if (node == nullptr)
return false;
TreeNode *p = findNum(root, k - root->val); // O(logN)
if (p == nullptr || p == node)
return fun(node->left, root, k) || fun(node->right, root, k);
else
return true;
}
bool findTarget(TreeNode *root, int k)
{
if (root == nullptr)
return false;
return fun(root, root, k);
}
};
4.三数之和
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/3sum

class Solution
{
public:
vector<vector<int>> threeSum(vector<int> &nums)
{
vector<vector<int>> result;
int len = nums.size();
if (len < 3)
return result;
sort(nums.begin(), nums.end()); //先转换成有序向量
for (int i = 0; i < len; ++i)
{
if (nums[i] > 0)
break; // 如果当前数字大于0,则三数之和一定大于0,所以结束循环
if (i > 0 && nums[i] == nums[i - 1])
continue; //去重
int L = i + 1;
int R = len - 1;
while (L < R)
{
int sum = nums[i] + nums[L] + nums[R]; //转换成两数之和的问题
if (sum == 0)
{
result.push_back({nums[i], nums[L++], nums[R--]});
while (L < R && nums[L] == nums[L - 1])
L++; //L跳过重复元素
while (L < R && nums[R] == nums[R + 1])
R--; //R跳过重复元素
}
else if (sum > 0)
R--; //sum(两数和)较大时,R左移
else
L++; //sum 较小时,L右移
}
}
return result;
}
};
5.和为S的连续正数序列
小明很喜欢数学,有一天他在做数学作业时,要求计算出9~16的和,他马上就写出了正确答案是100。但是他并不满足于此,他在想究竟有多少种连续的正数序列的和为100(至少包括两个数)。没多久,他就得到另一组连续正数和为100的序列:18,19,20,21,22。现在把问题交给你,你能不能也很快的找出所有和为S的连续正数序列? Good Luck!
思路:
- 同两数之和的双指针的思路。时间O(n),空间最坏 O(n)
class Solution
{
public:
vector<vector<int>> FindContinuousSequence(int sum)
{
vector<vector<int>> res;
if (sum < 3)
return res;
int small = 1;
int big = 2;
int curSum = small + big;
//当small > mid 时,自然就不会形成 == sum 的情况了
while (small <= sum / 2)
{
if (curSum > sum)
{
curSum -= small; //注意这里与下面的代码顺序不同
small++;
}
else if (curSum < sum)
{
big++;
curSum += big;
}
else
{
vector<int> tmp;
for (int i = small; i <= big; i++)
tmp.push_back(i);
res.push_back(tmp);
tmp.clear();
big++;
curSum += big; //继续移动 big ,找下一个序列!!!
}
}
return res;
}
};
- 拓展:
最接近的三数之和
中等
四数之和
中等
较小的三数之和