GroupBlog

1.

/* 题目描述
如果一个数列S满足对于所有的合法的i,都有S[i + 1] = S[i] + d, 这里的d也可以是负数和零,我们就称数列S为等差数列。
小易现在有一个长度为n的数列x,小易想把x变为一个等差数列。小易允许在数列上做交换任意两个位置的数值的操作,并且交换操作允许交换多次。但是有些数列通过交换还是不能变成等差数列,小易需要判别一个数列是否能通过交换操作变成等差数列
输入描述:
输入包括两行,第一行包含整数n(2 ≤ n ≤ 50),即数列的长度。
第二行n个元素x[i](0 ≤ x[i] ≤ 1000),即数列中的每个整数。
输出描述:
如果可以变成等差数列输出"Possible",否则输出"Impossible"。
示例1
输入
复制
3
3 1 2
输出
复制
Possible
*/

#include <bits/stdc++.h>
using namespace std;
int main(void)
{
    int n;
    cin >> n;
    vector<int> vv;
    int temp;
    while (n--)
    {
        cin >> temp;
        vv.push_back(temp);
    }
    sort(vv.begin(), vv.end());
    int len = vv.size();
    int sum = 0, tt = vv[1] - vv[0];
    for (int i = 2; i < len; i++)
    {
        if (tt != vv[i] - vv[i - 1])
        {
            cout << "Impossible" << endl;
            return 0;
        }
        tt = vv[i] - vv[i - 1];
    }
    cout << "Possible" << endl;
}

以上代码AC

2.

题目描述
小Q和牛博士在玩一个石子合并的游戏，初始一共有n堆石子，每堆石子有w[i]个石子。小Q和牛博士他们需要对石子堆进行合并，每次他们可以任意选择两堆石子进行合并。一堆有x个石子的石子堆和一堆有y个石子的石子堆合并将得到一堆x+y个石子的石子堆，这次合并得分为x*y，当只剩下一堆石子的时候游戏结束。

、小Q和牛博士希望采取优秀的策略获得最大得分，希望你能来帮他们算算最大得分多少。

输入描述:
输入包括两行，第一行一个正整数n(2≤n≤100)。

第二行包括n个正整数wi，即每堆石子的个数。
输出描述:
输出一个正整数，即小Q和牛博士最大得分是多少。
示例1
输入
复制
3
1 2 3
输出
复制
11 */

#include <bits/stdc++.h>
using namespace std;
//贪心,两个两个student一个桌子的问题
int main()
{
    int n;
    cin >> n;
    vector<int> vv;
    int temp;
    while (n--)
    {
        cin >> temp;
        vv.push_back(temp);
    }
    sort(vv.begin(), vv.end());
    for (auto i : vv)
        cout << i << "  ";
    cout << endl;
    int result = vv[0] * vv[1];
    int sum = 0;
    for (int i = 1; i < vv.size(); i++)
    {
        sum += vv[i - 1];
        result += vv[i] * sum;
        cout << "v[i] = " << vv[i] << "   " << sum << "  " << result << endl;
    }
    cout << result - 1 << endl;
}

以上代码AC 70%

别人通过的代码：

#include <iostream>
 
using namespace std;
 
int main() {
    int n; cin >> n;
    int stock = 0, score = 0;
    for(int curr; cin >> curr; ) {
        score += stock * curr;
        stock += curr;
    }
    cout << score;
}

证明：
其实顺序完全不影响的。无论什么顺序都是一样的结果。

设w1,w2,…,wn是一个任意的合并顺序（即先取w1，之后w1和w2合并，再之后w1 + w2,w3合并……）
在该合并顺序下的得分为：
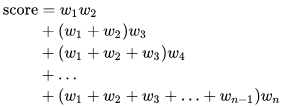
在这里插入图片描述
将上面的式子乘以二，再将含有w1,w2,…wn的项提出来（把下面的和上面的对比你会发现每一个都多用了一遍），得到：

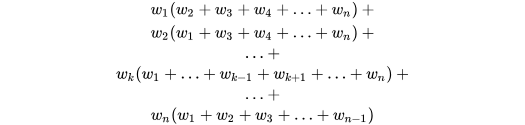
记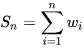，那么其实总得分就是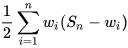，与具体序列的顺序无关，只与序列元素的值有关。