1.重建二叉树
题目:输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回
思路:前序(根左右)遍历的第一个节点就是根节点,于是我们在中序(左根右)遍历中找到该节点,于是该节点就把树划分成了左子树和右子树,之后递归求解即可
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution
{
public:
TreeNode *buildTree(vector<int> &preorder, vector<int> &inorder)
{
auto pre_size = preorder.size();
auto in_size = inorder.size();
if (pre_size != in_size || pre_size == 0 || in_size == 0)
return nullptr;
return fun(preorder, 0, pre_size - 1, inorder, 0, in_size - 1);
}
TreeNode *fun(vector<int> &preorder, int preL, int preR,
vector<int> &inorder, int inderL, int inderR)
{
if (preL > preR)
return nullptr;
TreeNode *root = new TreeNode(preorder[preL]);
int i = 0;
for (; i <= inderR; i++)
{
if (inorder[i] == preorder[preL])
break;
}
int left_size = i - inderL;
int right_size = inderR - i;
root->left = fun(preorder, preL + 1, preL + left_size,
inorder, inderL, i - 1);
root->right = fun(preorder, preL + left_size + 1, preR,
inorder, i + 1, inderR);
return root;
}
};
2. 中序遍历的下一个节点
题目:给定一个二叉树和其中的一个结点,请找出中序遍历顺序的下一个结点并且返回。注意,树中的结点不仅包含左右子结点,同时包含指向父结点的指针
思路:
- 如果一个节点有右子树,那么下一个节点就是它的右子树中的最左子节点
- 如果节点没有右子树,并且它是父节点的左子节点,则下一节点就是它的父节点
- 如果节点没有右子树,并且它是父节点的右子节点,则沿着指向父节点的指针一直向上遍历,直到找到一个是它父节点的左子节点。如果这样的节点存在,那么这个节点的父节点就是我们要找的下一个节点
class Solution
{
public:
TreeLinkNode *GetNext(TreeLinkNode *pNode)
{
if (!pNode)
return nullptr;
if (pNode->right) /*如果右节点没空,就去找右节点的最左边的节点即可*/
{
TreeLinkNode *temp1 = pNode->right;
while (temp1->left)
{
temp1 = temp1->left;
}
return temp1;
}
else /*右节点是空的*/
{
TreeLinkNode *temp2 = pNode;
while (temp2->next && (temp2 != temp2->next->left))
{
temp2 = temp2->next;
}
if (!temp2->next)
return nullptr;
else
return temp2->next;
}
}
};
3. 树的子结构
题目:
输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们约定空树不是任意一个树的子结构)
思路:
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};*/
class Solution
{
public:
bool HasSubtree(TreeNode *pRoot1, TreeNode *pRoot2)
{
if (!pRoot1 || !pRoot2)
return false;
bool ret = false;
if (pRoot1->val == pRoot2->val)
{
ret = (sametree(pRoot1->left, pRoot2->left) && sametree(pRoot1->right, pRoot2->right));
if(ret) return true;
}
return (HasSubtree(pRoot1->left, pRoot2) || HasSubtree(pRoot1->right, pRoot2));
}
bool sametree(TreeNode *t1, TreeNode *t2)
{
if (!t2)
{
return true;
}
else
{
if (!t1)
return false;
}
if (t1->val == t2->val)
return (sametree(t1->left, t2->left) && sametree(t1->right, t2->right));
else
return false;
}
};
4. 序列化二叉树
题目:实现两个函数,分别用来序列化和反序列化二叉树
题解:首先,前序遍历化为一个序列!
反序列化时,第一个就是root,之后前半部分是左子树,后半部分是右子树,遇到一个’#'就得回到前面去找其
class Codec
{
public:
// Encodes a tree to a single string.
string serialize(TreeNode *root)
{
if (root == nullptr)
return "#";
return to_string(root->val) + "," + serialize(root->left) +","+ serialize(root->right);
};
// Decodes your encoded data to tree.
TreeNode *deserialize(string data)
{
return fun(data);
}
private:
TreeNode *fun(string &data)
{
if (data == "")
return nullptr;
if (data[0] == '#')
{
data = data.substr(data.find(',')+1);
return nullptr;
}
size_t idx=0;
int x = stoi(data,&idx);
data = data.substr(idx + 1);
TreeNode *root = new TreeNode(x);
root->left = fun(data);
root->right = fun(data);
return root;
}
};
这是最骚的:
class Codec {
private:
TreeNode* _root;
public:
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
_root = root;
return string();
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
return _root;
}
};
7. BST的后序遍历序列
题目:输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同
后序遍历(左右根).最后一个节点一定是整个树的根节点,根据树与递归的关系,泛化而讲,他会是树的根节点(包括左子树,右子树等等).所以我们的思路就是先找到根,然后判断前部分(相当于左子树)是否小于根,后部分(相当于右子树)是否大于根即可
class Solution
{
public:
bool VerifySquenceOfBST(vector<int> sequence)
{
int sz = sequence.size();
if (sz == 0)
return false;
return IsBST(sequence, 0, sz - 1);
}
//第一部分是左子树结点的值,它们都比根结点的值小
bool IsBST(const vector<int> &sequence, int left, int right)
{
if (left >= right)
return true;
int mid, tp = left;
int root = sequence.at(right);
/*先找左子树*/
while (tp < right && sequence.at(tp) < root)
{
tp++;
}
if (tp < right)
{
mid = tp;
//第二部分是右子树结点的值,它们都比根结点的值大
// 查找右子树是否符合要求
while (tp < right)
{
if (sequence.at(tp) < root)
{
return false;
}
tp++;
}
}
// 递归的判断左右子树是否符合要求
return IsBST(sequence, left, mid - 1) && IsBST(sequence, mid, right - 1);
}
};
公共祖先
1. 两个节点的最低公共祖先
题目:
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
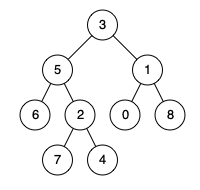
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。
思路:将root到两个点的路径保存下来,然后找到最后一个相同的节点,那这个节点就是最近的公共祖先(就是都经过该节点)
class Solution
{
public:
TreeNode *lowestCommonAncestor(TreeNode *root, TreeNode *p, TreeNode *q)
{
if (!root || !p || !q)
return NULL;
if (p == q)
return p;
dfs(root, p, q);
// 去找最后相同的第一个数字即可
// ....
if (paths.size() != 2)
return NULL;
int idx = 0 ;
while(paths[0][idx] == paths[1][idx])
idx++;
return paths[0][idx-1];
}
private:
void dfs(TreeNode *root, TreeNode *p, TreeNode *q)
{
if (!root)
return;
path.push_back(root);
if (root == p || root == q)
paths.push_back(path);
if (root->left)
dfs(root->left, p, q);
if (root->right)
dfs(root->right, p, q);
path.pop_back();
}
vector<vector<TreeNode *>> paths;
vector<TreeNode *> path;
};
6.关于树的深度的问题
(1)104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回它的最大深度 3 。
class Solution
{
public:
int maxDepth(TreeNode *root)
{
if (!root)
return 0;
int leftdepth = maxDepth(root->left);
int rightdepth = maxDepth(root->right);
return leftdepth > rightdepth ? leftdepth + 1 : rightdepth + 1;
}
};
(2)111. 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/
9 20
/
15 7
返回它的最小深度 2
class Solution
{
public:
int minDepth(TreeNode *root)
{
if (root == NULL)
return 0;
int left = minDepth(root->left), right = minDepth(root->right);
if (root->left && root->right)
return 1 + min(left, right);
else //只要有一方 左边或者右边 为空
return 1 + left + right;
/*
1.左空:1+0+右
2.右空:1+左+0
3.左右都空的:1+0+0
*/
}
};