关于他们的思想,这里就不再罗嗦了,直接 show you my code ,看题讨论 。
题目1:自然是最最经典的塔类问题啦(数字之塔 )
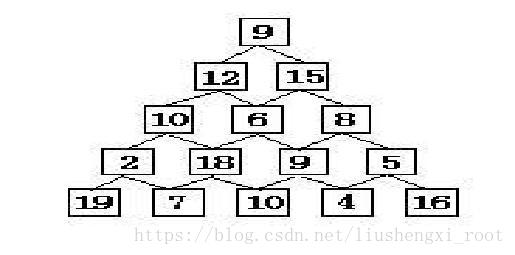
有如下所示的数塔,要求从顶层走到底层,若每一步只能走到相邻的结点,则经过的结点的数字之和最大是多少?
Input
输入数据首先包括一个整数C,表示数据的个数。
每个测试实例的第一行是一个整数N(1 <= N <= 100),表示数塔的高度,接下来用N行数字表示数塔,其中第i行有个i个整数,且所有的整数均在区间[0,99]内。
Output
对于每个测试实例,输出可能得到的最大和,每个实例的输出占一行。
Sample Input
1
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
Sample Output
30
解题思路:这类问题从塔的底层开始看起,从倒数第二层计算找到一个最大的和(倒数第二层与倒数第一层左右的和),比如:在这道题中,可以找到( 21,9,25,28,19,13,9,21),那么倒数第二层就会变成了(21,28,19,21)可以看出是目前从10->18最优,依次类推,下一步就会得到(31,38,34,25,27,29),那么倒数第三层就变成了(38,34,29),再下一步得到(50,46,49,44),,那么倒数第四层就变成了(50,49),以此类推即可。重点就是(局部最优,不一定整体最优)
#include <iostream>
#include <string.h>
#include<algorithm>
using namespace std;
#define TT 200 //整数 N(1 <= N <= 100),表示数塔的高度
int F[TT][TT];
int DP(int row)
{
for (int i = row - 2; i >= 0; i--)
{
for (int j = 0; j <= i; j++)
F[i][j] = max(F[i][j] + F[i + 1][j], F[i][j] + F[i + 1][j + 1]);
}
return F[0][0];
}
int main(void)
{
int C, N;
while (cin >> C)
{
for (int i = 0; i < C; i++)
{
memset(F, -1, sizeof(F));
cin >> N;
for (int j = 1; j <= N; j++)
{
for (int k = 0; k < j; k++)
cin >> F[j - 1][k];
}
cout << DP(N) << endl;
}
}
}题目2:B - 兑换硬币 + (DP || 数学)
在某个国家,只有 1 元、2 元和 3 元面值的三种硬币。现在你持有 N 元,想
把它全部兑换为硬币,请问有多少种兑换方法呢?
输入
输入的数据有多组,每组数据在一行内有一个正整数 N。
输出
对于每组数据,在一行内输出将 N 元换成硬币的方法数。
样例输入
2934
12553
样例输出
718831
13137761
DP 方法求解:
思路:递推即可
#include <iostream>
#include <vector>
using namespace std;
int DP(int amount)
{
vector<int> F(amount + 1, 1);
for (int i = 2; i <= 3; ++i)
{
for (int j = i; j <= amount; ++j)
{
F[j] += F[j - i]; //F[k]表示的兑换方法数
}
}
return F[amount];
}
int main(void)
{
int N = 0;
while (cin >> N)
{
cout << DP(N) << endl;
}
return 0;
}数学方法求解:有了数学,真的可以为所欲为。这句话真的没有一点毛病。先上AC代码看看:
#include <iostream>
#include <vector>
using namespace std;
int main(void)
{
int N = 0;
int temp ,Sum ,MM ;
while (cin >> N)
{
temp = N / 3; //不仅表示有多少个三,还表示有3和1的组合的种类与多少种
Sum = N / 3 + 1; // +1代表什么?代表用 1 所构成的兑换方法数
for (int i = 0; i <= temp; ++i)
{
MM = (N - i * 3) / 2; /* “/2”是什么意思? */
/* 代表用2和1的组合去换拿掉一个3时剩下的数,可是,
这又是为什么呐?为什么要拿掉一个三?不拿掉其他的?
*/
Sum += MM;
}
cout << Sum << endl;
}
return 0;
}情景叙述:这里我们就以10元钱为例,10元可以只由3和1的组合构成10/3种([3,3,3,1],[3,3,111,1],[3,111,111,1]),而由1构成的只有一种([111,111,111,1]),当然,在这时,我们也知道了它有多少(N/3)个三,这时我们求它只由2和1构成的数量(N/2),然后我们拿出来一个三(其实就是这个三不变了,其余的用2和1的组合代替),以此类推,我们再拿出来一个三,再拿出来一个三,再拿出来一个三,直到把三拿完即可。
PS:感觉这个结论,是具有普适性的,以后遇到再进行更加一步的证明。有待论证。
题目3,4:都是最长公共子序列的变式,以前写过,这里就不说了 。不会的可以点 这里
题目5:E - 超级跳跃 Remake
输入
输入的数据有多组,每组数据首先是两个正整数 N 和 M (1 ≤ N, M ≤ 100)
表示在一个 N × N 的区域内进行游戏,且超级跳跃只能移动到距离为 M 的区
域中。接下来有 N 行,每行有 N 个以空格为分dp
若 N 和 M 均cout << 等,表示输入结束,每组数据,在一行内输出一个正整数,表示游戏中可获得的最大价值。
样例输入
3 1
1 2 5
10 11 6
12 12 7
-1 -1
样例输出
37 */
解题思路:DFS+DP。DFS通过递归的手段从后向前找寻答案,而我们一般的DP从前向后寻找答案。这道题则采用 DFS+DP(记忆化搜索)的手段去解决。当前状态的值等于 Max(下一个状态1,下一个状态2,下一个状态3,下一个状态4 。。。)这里需要通过递归获得。
DP[i][j] 表示的就是从[i][j] 点开始所能吃到的最大奶酪数
#include <iostream>
#include <string.h>
#include <algorithm>
using namespace std;
const int TT = 101;
int map[TT][TT] = {0};
int dp[TT][TT] = {0};
/*用dp[i][j]表示以(i,j)为起点进行dfs的结果,从而下次扫到(i,j)时就不需要再扫一遍了。*/
int M = 0, N = 0;
int dir[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; //右,下,左,上
bool check(int x, int y, int xx, int yy)
{
if (xx < 0 || xx > N || yy < 0 || yy > N)
return false;
if (map[xx][yy] <= map[x][y]) // 判断条件
return false;
return true;
}
int DFS(int x, int y)
{
if (dp[x][y] > 0)
return dp[x][y];
int result = 0;
for (int i = 0; i < 4; i++)
{
for (int j = 1; j <= M; j++)
{
int xx = x + dir[i][0] * j;
int yy = y + dir[i][1] * j;
if (check(x, y, xx, yy))
{
result = max(result, DFS(xx, yy));
//printf("result == %d \n", result);
}
}
}
dp[x][y] = result + map[x][y];//从dp[x][y]开始能吃到的最大奶酪量
/*可以走各个点的最大值中最大的那个+当前点的数值 = 当前点的最大值*/
printf("dp[%d][%d] == %d\n", x, y, dp[x][y]);
return dp[x][y];
}
int main(void)
{
while (cin >> N >> M)
{
if (N == -1 && M == -1)
return 0;
memset(map, 0, sizeof(map));
memset(dp, 0, sizeof(dp));
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
cin >> map[i][j];
}
}
cout << DFS(0, 0) << endl;
}
}记忆化搜索与DP的区别:
DP是从下向上,而记忆化搜索是从上向下的
DP是从下向上,为了求到最终结果需要把过程中所有的值都保存下来,以便下一步可能会使用,而因为记忆化搜索是从上向下的,所以求解过程求的都是需要的;也就是说不需要的值并没有求
记忆化搜索使用递归实现的,而DP是使用迭代实现的
如果一个dp[i][j]的值已经求过,使用DP直接调用即可;而使用记忆化搜索则要进入递归中去求,而这个递归很有可能是多重的
题目6:F - 超级跳跃 2 + 排队问题
广受好评的《超级跳跃》游戏终于出了新作品,你作为它的粉丝已经迫不及
待的想要购买了。当你到达电玩店时,发现店前已经排起了长队,加上你一
共有 N 个人之多!每个人单独购买自己所需要的产品所需 Ki 秒,也可以选择
和排在自己前面的那个人合作,这样的话则需要 Si 秒。现在是早上 8 点,若
这 N 个人采用了最快的方式买完了自己所需的产品,那么买完的时候是什么
时间呢?
输入
输入的数据首先是一个整数 C,表示有 C 组输入数据。每组数据首先是一个
正整数 N(1 ≤ N ≤ 10),然后在下一行内有 N 个整数 K1,K2 … KN,表示 N
个人单独购买需要的时间,接下来有 N – 1 个整数 S1,S2 … SN-1,表示每个
人和前面那个人一起购买需要的时间。
输出
对于每组数据,在一行内输出 N 个人最快在何时全部完成购买。
输出格式为 HH:MM:SS am/pm,如开始时间就表示为 08:00:00 am,下午 2
时则表示为 14:00:00 pm。
样例输入
2
2
20 25
40
1
8
样例输出
08:00:40 am
08:00:08 am
解题思路:状态转移方程叙述:第n个人所用的时间就是 Min(前一个人所用的时间+第n个人单独用的时间,前n-2个人所用的时间+第n-1个人和第n个人时间和)
#include <iostream>
#include <string.h>
#include <algorithm>
#include <climits>
using namespace std;
const int TT = 2000;
int F[2][TT] = {0}; // 2 行 ,最大是 N 列
int dp[TT] = {0};
int DP(int n)
{
dp[0] = F[1][0];
dp[1] = min(F[0][0], dp[0] + F[1][1]);
for (int i = 2; i < n; i++)
dp[i] = min(dp[i - 1] + F[1][i], dp[i - 2] + F[0][i - 1]);
/*状态转移方程叙述:第n个人所用的时间就是
Min(前一个人用的时间+第n个人单独用的时间,前n-2个人所用的时间+第n-1个人和第n个人的时间和)*/
return dp[n - 1];
}
int main(void)
{
int C, N;
while (cin >> C)
{
for (int k = 0; k < C; k++)
{
cin >> N;
memset(F, 0, sizeof(F));
for (int i = 0; i < N; i++)
cin >> F[1][i];
for (int j = 0; j < N - 1; j++)
cin >> F[0][j];
int temp = DP(N);
int second = temp % 60;
int hour = temp / 60 / 60 + 8;
temp = temp / 60;
int minutes = temp % 60;
if (hour >= 12)
printf("%02d:%02d:%02d pm\n", hour, minutes, second);
else
printf("%02d:%02d:%02d am\n", hour, minutes, second);
}
}
}
