问题描述
把椅子往不平的地面一放,通常只有三只脚着地,放不稳,然而挪动几次,就可以使四只脚同时着地,放稳了。
模型假设
为了简化该问题,抛开一些非主干的问题,我们需要对问题做一些假设:
1. 假设椅子的四条腿一样长,椅子腿与地面接触处抽象为一个点
2. 椅子腿的四个点所构成的平面图形为正方形椅子腿的四个点所构成的平面图形为正方形
3. 地面高度是连续变化的,可以看做一个连续曲面
4. 地面是相对椅子平坦的,在任何时候椅子至少要能有三条腿着地(地面不会出现深沟或者凸峰)
模型构造
中心问题是用数学语言把椅子四条腿同时着地的条件和结论
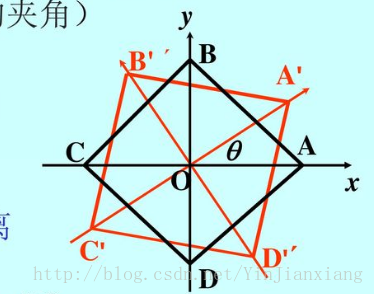
我们用椅子腿对角线 AC 与 x 轴的夹角 θ 来表示椅子的位置
其次,我们需要用数学语言来描述椅子腿距地面的距离,由于正方形的中心对称性,我们只需要设两个距离函数:
- A,C 两脚距离地面的距离和 f(θ)
- B,D 两脚距离地面的距离和 g(θ)
我们看到这两个函数都是关于椅子位置(θ)的函数,并且根据我们之前的假设3,我们可以知道这两个函数都是连续函数。
根据假设4(在任何时候椅子至少要能有三条腿着地),我们就可以得到,对于任意的 夹角 θ ,f(x) 与 g(x) 至少有一个为0,我们假设 g(x) = 0, f(x) > 0,由于正方形的中心对称性,当椅子转动90度后,于是 f(π/2) = 0, g(π/2) > 0
因此我们就把问题抽象为了一个数学命题,用数学语言描述如下:
已知 f(x) 和 g(x) 是关于 θ 的连续函数,对于任意的 θ ,f(x) * g(x) = 0 ,且 g(0) = f(π/2) = 0, f(0) > 0 , g(π/2) > 0 。证明:存在一个角度θ0,使得f(θ0) = g(θ0) = 0
模型求解
对于以上抽象出的问题就已经很简单了,只要我们证明出了以上命题就可以得到最后问题的答案。
我们试着证明一下上面的命题,其实根据命题我们就知道根据很简单的微积分中连续函数的基本性质就可以证明出来
证明: 令h(θ) = f(θ) - g(θ),则 h(0) > 0 h(π/2) < 0,由于 f(x) 和 g(x) 的连续性可知 h(x) 同样也是连续函数。根据连续函数基本性质,我们可以得到必存在 θ0(0 < θ0 < π/2)使h(θ0) = 0,即f(θ0) = g(θ0),最后,因为f(x) * g(x) = 0,得到f(θ0) = g(θ0) = 0
最终我们得到的结论是,在我们的假设的条件下,椅子能在不平的地面上放平。
扩展延伸
假设椅子腿的四个点所构成的平面图形为长方形
转自:http://www.chinadmd.com/file/xxawuzuvowzx66rtoiosrwwv_1.html


