Scrooge McDuck keeps his most treasured savings in a home safe with a combination lock. Each time he wants to put there the treasures that he's earned fair and square, he has to open the lock.

The combination lock is represented by n rotating disks with digits from 0 to 9 written on them. Scrooge McDuck has to turn some disks so that the combination of digits on the disks forms a secret combination. In one move, he can rotate one disk one digit forwards or backwards. In particular, in one move he can go from digit 0 to digit 9 and vice versa. What minimum number of actions does he need for that?
The first line contains a single integer n (1 ≤ n ≤ 1000) — the number of disks on the combination lock.
The second line contains a string of n digits — the original state of the disks.
The third line contains a string of n digits — Scrooge McDuck's combination that opens the lock.
Print a single integer — the minimum number of moves Scrooge McDuck needs to open the lock.
5 82195 64723
13
In the sample he needs 13 moves:
- 1 disk:

- 2 disk:
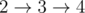
- 3 disk:

- 4 disk:

- 5 disk:
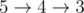
#include<stdio.h>
int main(void){
int i;
int m;
int n;
int s=0;
char a[1002],b[1002];
scanf("%d",&n);
scanf("%s",&a);
scanf("%s",&b);
for (i = 0;i < n;i++){
m = a[i] - b[i];
if (m < 0) {
m = -m;
}
if (m > 5) {
m = 10 - m;
}
s+=m;
}
printf("%d\n",s);
return 0;
}