动态规划之切割绳子

/*
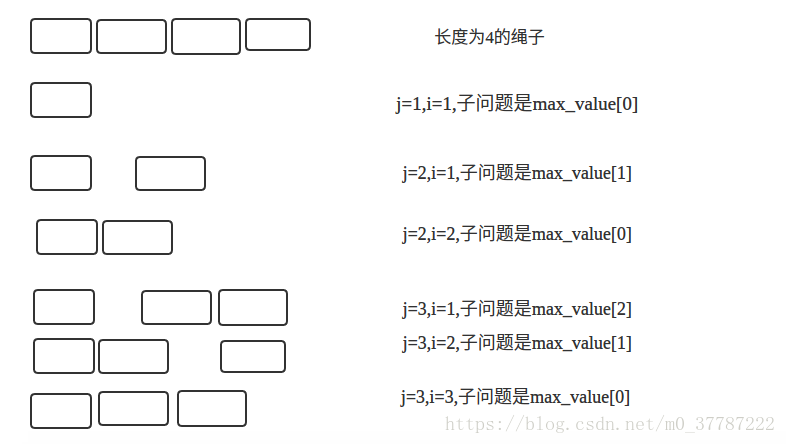
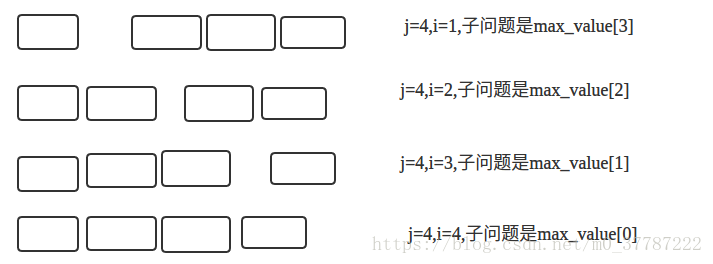
    切割绳子，每段绳子都有一个最大值，给定长度为n的绳子，如何切割让利益最大化
    自底而上的方法，对于任何子问题，直至它依赖的所有子问题都解决，才会去解决它。
*/
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
vector<int> max_value(100,0);//当长度为n时，最大利益
vector<int> first_cut(100,0);//当长度为n时，切割一刀的位置
vector<int> price{0,1,5,8,9,10,17,17,20,24,30};//每段绳子的价值
void cut_rope(int n)
{
    int max;
    max_value[0] = 0;//长度为0，值为0;
    for(int j = 1;j <= n;j++)//总长度
    {
        max = -1;
        for(int i = 1;i <= j;i++)//第一刀的长度
        {
            if(max < price[i] + max_value[j-i])//切割长度为i时的价值加上剩余长度的价值最大
            {
                max = price[i] + max_value[j-i];
                first_cut[j] = i;//长度为j时切第一刀的位置
            }
        }
        max_value[j] = max;//长度为j的时候，最大值为
    }
}
void print_cut_rope_solution(int n)
{
    cut_rope(n);
    cout <<"最大值为:"<<max_value[n]<<endl;
    cout <<"切割方案为:";
    while(n > 0)
    {
        cout << first_cut[n]<<" ";
        n = n-first_cut[n];
    }
}
int main()
{
    cout <<"请输入绳子长度:";
    int n;
    cin >>n;
    print_cut_rope_solution(n);

    return 0;
}

每个子问题说白了就是上一次求解的所有子问题的和