GroupBlog

一个思考题

在利用DFS和BFS遍历图时，有没有考虑过能不能在出队（栈）时访问元素呢？访问在前有什么好处呢？

BFS依靠队列来实现，以BFS来简单说一下吧

访问在前

void BFS(Graph g , int v0)
{
    visit(v0); //访问在前
    visited[v0] = 1;
    InitQueue(&Q);
    EnterQueue(&Q,v0);           //入队
    while(! Empty(Q)){
        DeleteQueue(&Q,&v);     //出队
        w = FirstAdjVex(g,v);       //图g中顶点v的第一个邻接点
            while(w!=-1){
                if(!visited(w)){
                visit(w);
                visited[w] = 1;
                EnterQueue(&Q,w);
            }
            w = NextAdjVex(g,v,w);
            //图g中顶点v的下一个邻接点
        }
    }
}

过程模拟

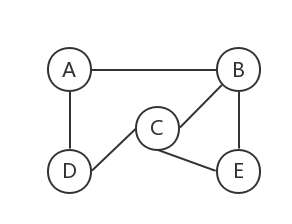
访问A并使A入队

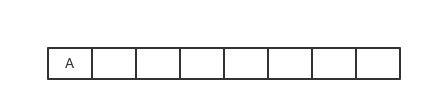
A出队，获得A的临接点有B、D且两者均没有被访问过，则访问B、D并使它们入队

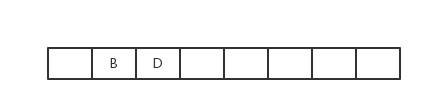
B出队，获得B的临接点有A、C、E，其中C、E没有被访问过，则访问C、E并使它们入队

D出队，获得D的临接点有A、C且两者均被访问过，则不操作

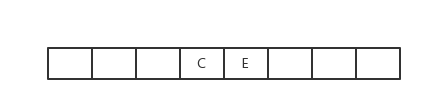
C出队，获得C的临接点有B、D、E且三者均被访问过，则不操作

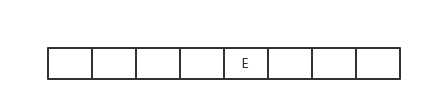
E出队，获得E的临接点有B、C且两者均被访问过，则不操作

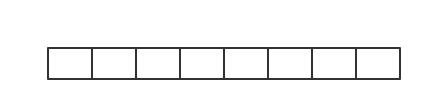
此时队列为空，一次遍历结束

注意：如果还有其它结点未被访问（非连通图），要选择一个未被访问的结点重复以上操作

访问在后

void BFS(Graph g , int v0)
{
    InitQueue(&Q);
    EnterQueue(&Q,v0);           //入队
    while(! Empty(Q)){
        DeleteQueue(&Q,&v);//出队
        visit(v);
        visited[v] = 1;    //访问在后
        w = FirstAdjVex(g,v);       //图g中顶点v的第一个邻接点
            while(w!=-1){
                if(!visited(w)){
                    EnterQueue(&Q,w);
            }
            w = NextAdjVex(g,v,w);
            //图g中顶点v的下一个邻接点
        }
    }
}

过程模拟

A入队

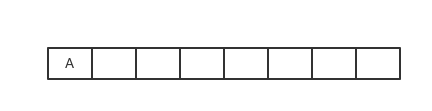
A出队，访问A，获得A的临接点有B、D且两者均没有被访问过，则使它们入队

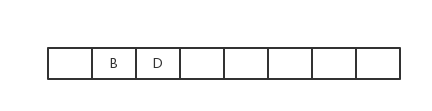
B出队，访问B，获得B的临接点有A、C、E，其中C、E没有被访问过，则使它们入队

D出队，访问D，获得D的临接点有A、C，其中C没有被访问过，则使它入队

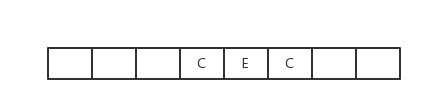
C出队，访问C，获得C的临接点有B、D、E，其中E没有被访问过，则使它入队

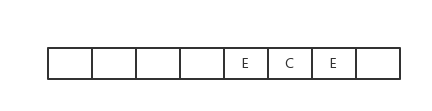
E出队，访问E，获得E的临接点有B、C且两者均被访问过，则不操作

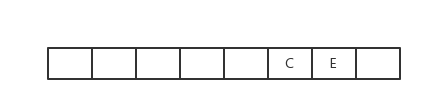
C出队，C已被访问，无操作
获得C的临接点有B、D、E且三者均被访问过，则不操作

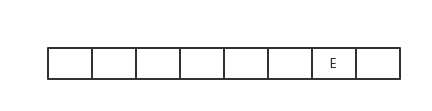
E出队，E已被访问，无操作
获得E的临接点有B、C且两者均被访问过，则不操作

此时队列为空，一次遍历结束

如果还有其它结点未被访问（非连通图），要选择一个未被访问的结点重复以上操作

总结

通过上面的两种访问元素的先后顺序，可以发现，如果我们在出队时访问元素，那么不可避免在队列中会出现重复的元素，而我们只访问一次就够了，后面的相当于空操作，浪费时间和空间，没有任何意义。如果我们不是有条件的访问，结果也会我们预想的很大差别，一个元素会被重复访问。所以，要在入队前访问元素。

DFS用栈来实现，如果在出栈时访问元素，也会造成栈中会存在相同元素，最终无意义的操作，浪费时间和空间，所以，要在入栈前访问元素。