GroupBlog

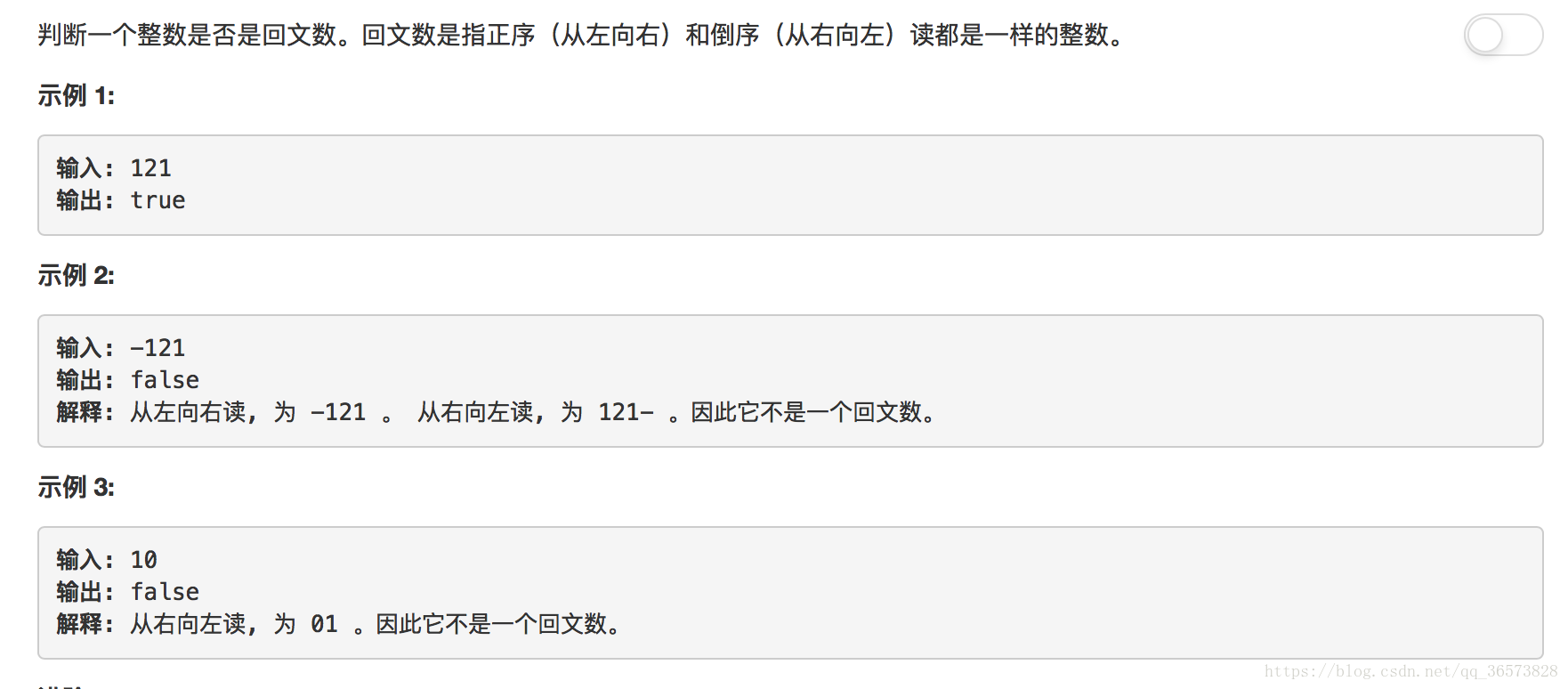
一、题目描述

二、思路

（1）可以将该整数转换成字符串，根据字符串的长度奇偶性来确定中间位置，然后首尾进行对比是否是回文数字。此时需要额外空间来存储字符串，然后进行判断

（2）可以将整数的最后一半数字进行整数反转，然后将反转的部分与数字的前部分进行比较，判断是否是回文数。也可以将整个整数进行反转然后进行比较，但是会发生溢出情况，所以可以选择只反转数字的后半部分，若与前半部分相同则为回文数。

我选择的方案是只对后半部分的数字进行反转，但是反转的停止点是反转的数字是否反转了一半的判断。

根据题目中的描述，若该整数是一个负数那么肯定不是回文数，或者该整数的最后一位为0而第一位不为0也不可能是回文数，所以可以直接将这两种情况判断返回false。此时剩下的普通情况的话，此处分为两种情况，若假设该数字是一个回文数，若是回文数的话，长度又分为奇数和偶数。若该整数长度为奇数的话那么反转一半的标志就是反转的数字与目前剩下的前面的那部分数字相同了，此时应停止反转；若该回文整数长度为偶数的话，我们将中间的那个元素归在反转数字中（例如：12321 我们一直将从1一直反转到3才停止）此时的话反转后的数字123大于了目前剩下的12的时候停止反转。若假设该数字不是一个回文数字，其中若整数长度无论是偶数还是奇数，进行反转的时候，反转的数字和目前前半部分剩下的数字永远不可能相等的，所以停止反转的标志就是当反转的数字大于目前前半部的数字的时候，停止反转。停止反转后，我们只需要将反转的结果和目前剩下的前半部分进行对比就行。在此处，若该数字是回文数的话，长度并且为奇数的时候（之前回文数长度为奇数的时候，我们反转的时候是将中间的那个数字算了进去），所以在最后进行对比的时候，要将反转的数字／10，再与前半部分的数字进行对比才可以，若该回文数长度是偶数的话，只需要将反转数和前半部数字直接对比就可以。而若该数字不是回文数的话，无论是奇数还是偶数长度，它都是不可能满足以上两种可能的，所以若都不满足以上的两种情况的话就说明该数字不是回文数。

三、代码实现（方法二）

class Solution {
public:
    bool isPalindrome(int x) {
        int sum=0;
        if(x<0 || (x/10!=0 && x%10==0))
        {
            return false;
        }
        else{
           while(x>sum)
           {
               sum  = sum * 10 + x%10;
               x = x/10;
           }
        }
        /*若整数为偶数*/
        if(sum == x)
        {
            return true;
        }
        /*若整数位数为奇数*/
        if(sum/10 == x)
        {
            return true;
        }
        return false;
    }
};

四、时间空间复杂度

（1）时间复杂度

对于每次迭代，我们会将输入除以10，因此时间复杂度为 $O(log10(n))$ 。

（1）空间复杂度

O(1)