给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:
输入: [7,6,4,3,1] 输出: 0 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
看到这道题,首先我想着使用贪心算法,但是并不合适!
想了好久,知道使用动态规划可以做!
在看了解答之后,才发现这个问题使用牛顿莱布尼茨公式来解决。
设数组中的第n个元素为F[n],则要求的是
MAX(F[m]-F[n])的值,我们可以有牛顿莱布尼茨公式:
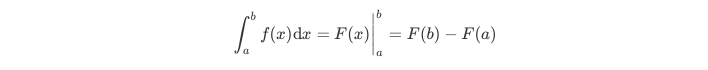
这里,F()函数不是连续的,而是离散的,a和b表示数组的下标。
所以我们只需要求出的值:
a[i]-a[j]=a[i]-a[i-1]+a[i-1]-a[i-2]+…+a[j+1]-a[j]=dif[i]+dif[i-1]+…+dif[j+1]
即代码实现:
int maxProfit(vector<int>& prices) {
if (prices.size() <= 1) return 0;
vector<int> diff(prices.size() - 1);
for (int i = 0; i < prices.size() - 1; ++i) {
diff[i] = prices[i+1] - prices[i];
}
int last = 0;
int profit = last;
for (int i = 0; i < diff.size(); ++i) {
last = max(0, last + diff[i]);
profit = max(profit, last);
}
return profit;
}