题目描述:东东在一本古书集上看到一个神奇数(大于0),如果能够将一个数的所有位的数分成两组数,其中一组数字之和等于另一组数字的和,那这个数就是神奇数。现在给定一个取值范围,求该范围中神奇数的个数!
数字224,可以分为(2,2)和(4)两组数字相等,符合神奇数的要求。
数字123可以分成(1,2)和(3)所以是神奇数。
234 无论那种分发都不能分成和相等的两组数,所以不是神奇数。
对于这个问题,我们需要先要拆分这个数中每一位存到数组中,并对这些数字进行求和。
我们所设置的数字上限是9999999999!则我们需要设置一个长度为46的数组(在此不考虑类型,因为不是重点)。
为什么要开长度为46的数组?这个看完下面你就知道了。
这个题的解决方法按照我的理解就是将每组数字的加操作用数组的变化来表现出来。
先通过一个简单例子来慢慢理解我上面所述的那句话:
这里有一个元素全为false的bool数组a,还有一个存有一些整型数字的数组tmp。现在要求出整型数组中所有元素的和,并通过查询数组a得到结果。如何解决?
设置sum=0,从tmp中元素为0开始,sum加上tmp[0],设置a[sum]=true,这样依次改变a中的元素即可;
//这里为伪代码
int sum = 0;
//假设len为数组长度
for(int i=0;i<len;i++)
{
sum += tmp[[i] ;
a[sum]=true ;
}
int index = 0 ;
最后只需要找最后一个部位true所在a中的下标即可,这个下标就是数组tmp中所有元素的和。
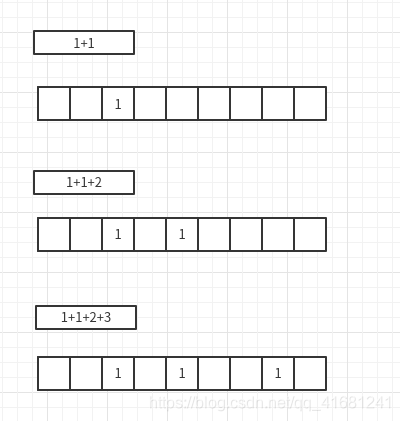
过程就是上图中的过程!
下面我们看一下神奇数问题的解决。
我们假设要判断最大的神奇数上限是9999999999,当然这个数一看就是神奇数,将每一位分离,然后分成两个组,每组为5个9,两边和都为45。对于9999999999这个数,分组后,其中一个组的总和在bool数组array中表示出来的话:
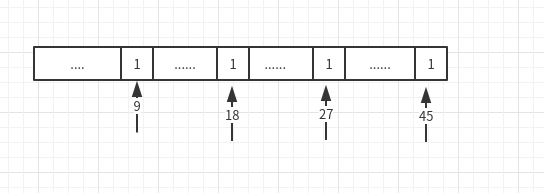
array[45]的值是1,由此判断9999999999这个数是神奇数。
所以我们用同样的方式来判段其他数是否为神奇数。这时候看为什么将数组长度置为46,因为比如数字为9999999999的话
,判断的数将每一位分成两组后,每组求和,判断和是否为45。即当array[45]=1时,则得出该数为神奇数。
经过以上分析,对于任何数,将他的分成任意两组,只要判断其中一组的和是否为sum/2,也就是我们只关心bool数组array[sum/2]是否为true即可(sum为这个数的每一位数相加的总和,且sum为偶数这也是满足神奇数的前提条件,我们初始化bool数组全为false),只要array[sum/2]为true那么就说明存在一个子序列纸盒为sum/2,也就是这个数是神奇数!
#include <iostream>
using namespace std ;
bool check(int num)
{
int sum = 0 ;
int a[20] ;
int cur = 0 ;
while(num>0)
{
a[cur] = num%10 ;
sum += a[cur++] ;
num=num/10 ;
}
if(sum%2 !=0)
{
return false ;
}
int t = sum/2 ;
bool tmp[46] ={0};
tmp[a[0]] = 1 ;
for(int i=1; i<cur; i++)
{
int index = a[i] ;
for(int j=45; j>=0; j--)
{
if(tmp[j] && j+index<46)
{
tmp[j+index] = 1 ;
}
}
if(tmp[t] == 1)
{
return true ;
}
}
return false ;
}
int main()
{
int counts = 0 ;
int m,n ;
cin >> m >> n ;
for(int i=m; i<n; i++)
{
if(check(i))
{
cout << i << endl ;
counts ++ ;
}
}
cout << counts << endl ;
return 0;
}
还有一种方法是递归比较好理解:
#include <iostream>
using namespace std;
bool isMagicArr(int index, int sum, int* nums)
{
if (sum == 0) // 递归结束条件1
return true;
if (sum < 0 || index < 0) // 递归条件结束2, 累加和超过了或者数组中没有值了
return false;
// num[index]是sum中的一部分或者不是sum中的一部分
return isMagicArr(index - 1, sum - nums[index], nums) || isMagicArr(index - 1, sum, nums);
}
bool checkMagic(int num)
{
int nums[11]; // 把数字num按位存到nums中
int index = 0;
int sum = 0; // 每位数字求和
for ( ; num > 0; index++)
{
nums[index] = num % 10; // 获取并保存每位数字
sum += nums[index]; // 每位数字累计求和
num = num / 10; // 除去个位数字
}
// 每位数和是奇数,则肯定不是神奇数
if (sum % 2 != 0)
return false;
return isMagicArr(index, sum / 2, nums);
}
int main()
{
int l = 0, r = 0;
cin >> l >> r;
int start = clock() ;
int count = 0;
for (int num = l; num <= r; num++)
{
if (checkMagic(num)){
cout <<num <<endl ;
count++;
}
}
cout << "神奇数总数:"<<count << endl;
int end =clock() ;
cout <<"总耗时:"<<end-start<<endl ;
return 0;
}
以上两种方法在时间上开销是差不多的!