二叉搜索树学习

原 作者 畅柯 | 发表于 | 分类于 2017级

二叉搜索树：对于二叉搜索树，若左孩子不为空，父亲节点的值大于左孩子的值；若右孩子不为空，则右孩子的值大于父亲节点的值。
就像下面这个图一样：
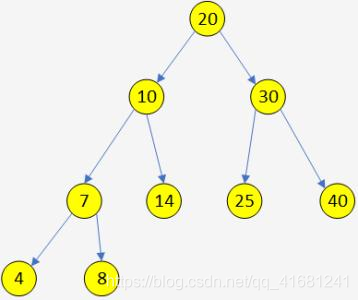
在这里插入图片描述

二叉搜索树的创建和插入
本篇文章主要总结二叉搜索树的创建和插入，删除的话，感觉没啥用，就不想写了。

创建
创建的话，和二叉树的创建区别就那么一丢丢，只不过得加个判断，根据性质，左孩子值要比父亲节点小，右孩子值要比父亲节点大，所以加个判断。

判断根节点是否为空，不为空的话，当添加的节点比当前节点要大的话，向右创建节点；否则向左添加节点；为空的话，直接创建新节点将数据存入。

  //添加新元素
    shared_ptr<node> build(shared_ptr<node>root, int e)
    {
        if(root == NULL)
        {
            size ++ ;
             shared_ptr<node>p = make_shared<node>(e) ;
             return p ;
        }
        else
        {
            if(e > root->a)
            {
                root->r = build(root->r, e) ;
            }
            else
            {
                root->l = build(root->l, e) ;
            }
        }
        return root ;
    }

插入
插入操作的话，有两种方式：

  • NO.1
    传入数据

判断要是比当前节点大的话，将其插入到当前节点的右子树，当然别忘了比较插入的数据和右孩子节点的数据的大小，右孩子节点的值比插入数据大，将右孩子作为插入数据的右孩子，作为插入数据的左孩子。

否则，将数据插入到左子树，同样插入节点与当前节点右孩子数据进行比较，并决定将当前节点的左孩子作为插入数据的左孩子还是右孩子。

总之，一定得遵循文章刚开始所将的原则，才能维护好二叉搜索树。
如图所示：
在这里插入图片描述这样插入的好处就是方便快捷。

  • NO.2
    我想我们应该都会发现，上一种做法插入时间复杂度为O(1)，随着数据的增多，很可能会使我们的二叉搜索树退化为链表，那我们岂不是白忙活！
    对上一种插入方法，我是拒绝的！！！
    所以我的插入操作是用下面这种方法：

继续从头结点开始，比较当前结点数据和插入数据的值，
比插入数据大的话:

  • 判断当前节点的右子树是否为空，为空的话，直接将要插入的节点查到当前节点的右子树位置。
  • 要是不为空
    • 比较插入节点和右子树数据的值，要是也大于等于右子树数据的话，就直接向右子树递归。
    • 要是小于右子树节点，将所插入的数据和当前节点数据进行交换，向左递归比较。

要是当前节点比插入数据小的话，向左类似于向右。

我觉得这种做法插入时间复杂度为o(logn)，但是他一直维护着这个二叉搜索树不会退化成链表。

下面是过程图：
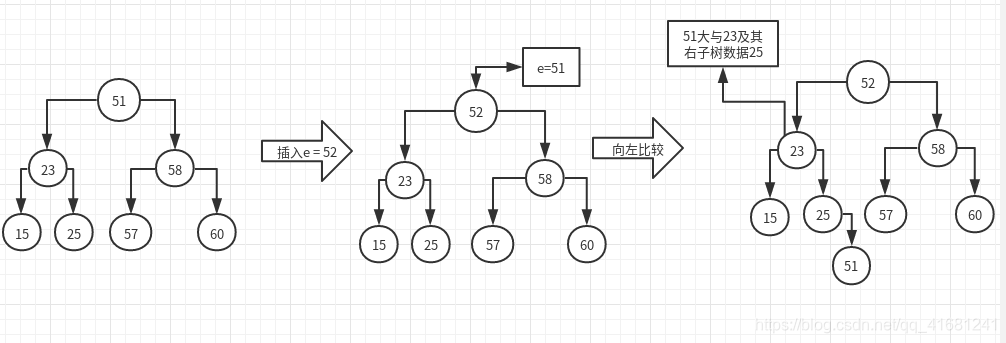
在这里插入图片描述
以上是部分过程图，要是看不懂的话下面是实现和测试代码，也许能帮助理解这个过程，遍历过程是二叉树的前序遍历。

#include <iostream>
#include<memory>
using namespace std ;
//二叉搜索树的学习

class node
{
    
    public :
        shared_ptr<node>l ;
        shared_ptr<node>r ;
        int a ;
    public :
        node()
        {
            a = 0 ;
            l = NULL ;
            r = NULL ;
        }

        node(int e)
        {
            a = e ;
            l = NULL ;
            r = NULL ;
        }

        ~node()
        {
            l = NULL ;
            r = NULL ;
        }
};

class BST: public node 
{
private :
    shared_ptr<node>root ;
    int size ;
    int a ;
public : 
    BST()
    {
        node() ;
        root = NULL ;
        size = 0 ;
    }
    
    ~BST()
    {
    }

public :
    void build()
    {
        int e ;
        while(1)
        {
            cin >>e ;
            if(e != -1)
            {
                root = build(root, e) ;
            }
            else 
            {
                break ;
            }
        }
    }

    //添加新元素
    shared_ptr<node> build(shared_ptr<node>root, int e)
    {
        if(root == NULL)
        {
            size ++ ;

             shared_ptr<node>p = make_shared<node>(e) ;
            
             return p ;
        }

        else
        {
            if(e > root->a)
            {
                root->r = build(root->r, e) ;
            }

            else 
            {
                root->l = build(root->l, e) ;
            }
        }

        return root ;
    }       

    void print()
    {
        print(root) ;
    }

    void print(shared_ptr<node>root)
    {
           if(root)
           {        
                cout << root->a <<endl ;
                print(root->l) ;
                print(root->r) ;
           }
    }
    
    //向树中插入元素
    void add(int e)
    {
        root = add(root, e) ;
        cout << "插入元素"<<e<<"后:" << endl ;
        print(root) ;
    }

    shared_ptr<node> add(shared_ptr<node>root, int e)
    {
        if(root == NULL)
        {
            return shared_ptr<node>(new node(e)) ;
        }
        else
        {
            if(e < root->a)
            {
              
                if(root->l == NULL)
                {
                    root->l = add(root->l, e) ;
                }

                //要是e不小于当前节点的左孩子数据
                if(e > root->l->a)
                {
                    swap(root->a, e) ;
                    add(root->r , e) ;
                } 

                if(e <= root->l->a)
                {
                    add(root->l, e) ;
                }
            }

            else if(e > root->a)
            {   
                if(root->r == NULL)
                {
                    root->r = add(root->r, e) ;
                }

                if(root->r->a > e)
                {
                    swap(root->a, e) ;
                    add(root->l, e) ;
                }

                if(root->r->a <= e)
                {
                    add(root->r, e) ;
                }
            }

            else
            {
                add(root->r, e) ;
            }
        }

        return root ;
    }

    void swap(int& old_, int& new_)
    {
        int temp = old_ ;
        old_ = new_ ;
        new_ = temp ;
    }

    //删除元素，感觉不常用，所以偷懒不写了！！！
    //思路：
    //1.当有左右孩子时
    //将左子树的最大节点或者右子树的最小节点调到当前节点位置即可这里省略了....
    //2.当没有左右孩子时，将当前节点指向空
    //3.当仅有右孩子或者左孩子，将当前节点的父亲节点指向该节点的左子树或者右子树即可
};

int main()
{
    BST bst ;
    //创建搜索树
    bst.build() ;
    bst.print() ;
	//插入40
    bst.add(40) ;
}

测试数据及结果

51 23 58 15 25 60 57 12 19 27 30 -1
51   23   15   12   19   25   27   30   58   57   60   
插入元素40后:
40   23   15   12   19   25   27   30   58   57   51   60