搜索算法在实际编程应用中起着举足轻重的作用,学会掌握搜索算法并熟练应用搜索算法来解决实际问题不得不说是一件相当COOL的事,所以我将深度搜索和广度搜索认真地做了详细的总结,与诸君共勉,也方便以后查阅复习
广度优先搜索(BFS)
顾名思义,追求的是”覆盖面积”,
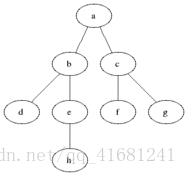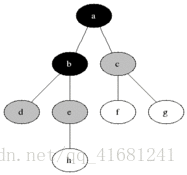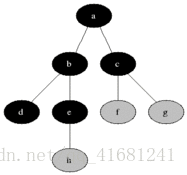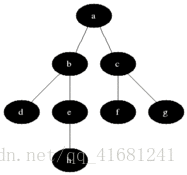
现在来一张简单的有向图,广度搜索就是按照那个顺序搜索的,像有句话所说,道生一,一生二,二生万物!
- 具体思想:从图中某顶点a出发,在访问了a之后依次访问a的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问,直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止。
换句话说,广度优先搜索遍历图的过程是以a为起点,由近至远,依次访问和a有路径相通且路径长度为1,2…的顶点,一般用数据结构中的队列来解决比较方便。
用途:求最短路径或最优方案
举个例子吧:
5 X 5迷宫问题
定义一个二维数组:int maze[5][5] = {
0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0,};
它表示一个迷宫,其中的1表示墙壁,0表示可以走的路,只能横着走或竖着走,不能斜着走,要求编程序找出从左上角到右下角的最短路线。
Input
一个5 × 5的二维数组,表示一个迷宫。数据保证有唯一解。
Output
左上角到右下角的最短路径,格式如样例所示。
Sample Input0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
Sample Output
(0, 0)
(1, 0)
(2, 0)
(2, 1)
(2, 2)
(2, 3)
(2, 4)
(3, 4)
(4, 4)
这是一个简单的算法题,可以尝试用广度优先的算法来解决它!
对于这个题我们该怎样下手呢~~~他找的是最短路径,方法很简单,用广搜,从起始坐标为(x0,y0), a[x0][y0]不为1的点开始,在遍历后,遍历第二个点之前,将第一个点a[x0][y0]赋值为1,并将a[x0][y0].next=NULL,后面的a[x1][y1].next=&a[x0][y0]以此类推后面的,这个作为到达终点后,用循环从终点往起点返回,保存(这一路走来)坐标数据的终止条件。这个点的数据加到队列中,遍历下一个节点前,将上一个结点以结构体指针形式弹出队列,因为要根据这个点来判断a[xp-1][yp-1],和a[xp][yp+1],a[xp+1][yp],a[xp][yp-1]是否为0,来决定向哪个方向走,凡是a[xx][yy]不为1的点都要遍历,每次遍历一个点就改变他的状态并将这个点加入到队列中a[xx][yy].next,当遍历的点的坐标都等于目的地的坐标时,终止,又往回走吧!
不纸上谈兵了,由于C语言用广度优先代码量比较多一点,我直接讲我的代码吧,或许更容易理清思路:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define N 100
int head ,rear ,num = 0;
typedef struct node{
int x , y ;//坐标
struct node * next ;
} node_t;
node_t b[N],way[N] ;//队列b,和记录路的座标的结构体数组
void go_map();
void cover() ;
void init();
void print();
node_t * pop();
int a[N][N];//构造地图
int main(){
while(1){
memset(a , 0 , sizeof(a));
int i , j ;
for( i =1 ; i< 6 ; i ++){
for( j = 1 ; j < 6; j++) {
if(scanf("%d",&a[i][j]) == EOF){//传入地图
//数据,注意这儿是从a[1][1]开始存的,后面将地图边缘用1围起来
return 0;
}
}
}
cover();
init();//初始化队列
go_map();
print();
}
return 0;
}
void print(){
int i;
for(i = num-1 ; i >= 0 ; i--){//打印最短路径
printf("(%d, %d)\n",way[i].x,way[i].y);
}
}
void cover(){//将整个地图外围用1围起来,方便搜索
int i , j ;
for( i = 0 ; i< 7 ; i++){
for( j = 0 ;j < 7 ; j++){
if( i == 0 || i == 6 || j == 0 || j == 6){
a[i][j] = 1;
}
}
}
}
void init(){//初始化队列
head = 0;
rear = 0;
}
node_t * pop(){//弹出队列成员
node_t * p ;
p = &b[head];
head ++;
return p ;
}
void record(int x ,int y ,node_t * next){//将走过的点信息加入队列,next为指向
//上一个节点数据的指针
b[rear].x = x;
b[rear].y = y;
b[rear].next =next ;
rear ++;
}
void go_map(){//遍历地图
node_t * temp ;
record(1,1,NULL);
while(1){
if(head >=rear )return ;//当队头和队尾相等时,退出
temp = pop();
if( temp -> x == 5 && temp->y == 5){//当走到终点时,用way 数
//组又保存返回到起点的路径
while(temp != NULL){//将第一个数据的next 指针指向空,
//作为返回起点的终止条件。
way[num].x = temp->x-1;
way[num].y =temp->y-1 ;
num ++ ;
temp = temp->next;
}
return ;
}
if(a[temp->x][temp->y - 1]!= 1)//遍历四个方向,只要满足条件,
//就加入队列
{
record(temp->x , temp->y -1 ,temp);
a[temp->x][temp->y - 1] = 1 ;
}
if(a[temp->x][temp->y + 1]!=1){
record(temp->x ,temp->y + 1 ,temp);
a[temp->x][temp->y + 1] = 1;
}
if(a[temp->x-1][temp->y]!= 1){
record(temp->x- 1 ,temp->y , temp);
a[temp->x - 1][temp->y] = 1;
}
if(a[temp->x + 1][temp->y]!= 1){
record(temp->x + 1 ,temp->y ,temp);
a[temp->x + 1][temp->y] = 1;
}
}
}现在对这个题还有那不懂的,可以留言交流,可能讲的不是很清楚,有意见欢迎提出!
凡是涉及最值的用广搜优势是比较突出的!
深度优先搜索(DFS)
重在追求”专一”吧!一条道走到黑
看这个无向图吧:
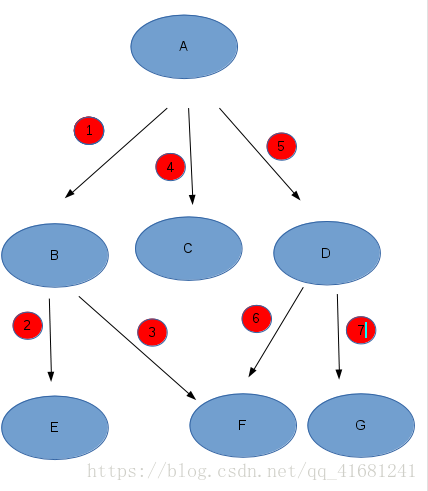
用深搜从A开始该怎样遍历呢?
A -> B ->E ->F ->C ->D ->G
图中我也按照序号从小到大遍历,就是这样子!按照递归,先沿着一条道走到黑,撞到南墙后,再返回一层,找另一条路继续走,不停返回,不停深入。
- 具体思想:
①访问顶点a;
②依次从a的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和a有路径相通的顶点都被访问;
③若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。
这有个问题:
不规则棋盘问题
在一个给定形状的棋盘(形状可能是不规则的)上面摆放棋子,棋子没有区别。要求摆放时任意的两个棋子不能放在棋盘中的同一行或者同一列,请编程求解对于给定形状和大小的棋盘,摆放k个棋子的所有可行的摆放方案C。
Input
输入含有多组测试数据。
每组数据的第一行是两个正整数,n k,用一个空格隔开,表示了将在一个n*n的矩阵内描述棋盘,以及摆放棋子的数目。 n <= 8 , k <= n
当为-1 -1时表示输入结束。
随后的n行描述了棋盘的形状:每行有n个字符,其中 # 表示棋盘区域, . 表示空白区域(数据保证不出现多余的空白行或者空白列)。
Output
对于每一组数据,给出一行输出,输出摆放的方案数目C (数据保证C<2^31)。
Sample Input
2 1
#.
.#
4 4
...#
..#.
.#..
#...
-1 -1
Sample Output
2
1
这个题刚开始我看了也束手无策,甚至不知道它什么意思,此处应该哭笑一波……根本不会想到用深度优先,弄懂它以后,才豁然开朗,它第一个参数是行列数,设置好后,随便摆棋子,第二个是符号“#”的个数,设置好行列数n后,建立二维数组,输入n组含“#“的字符串,且输入的字符串中的“#”要多与你第一个参数设置的“#”数量,根据深度优先算法每次遍历一个字符,判断它是否是“#”,若是,则将你设定的记录次数+1,(由于原题规定设定的棋子不能在同一行同一列,所以下面讲的代码,是遍历按照列数多少记录棋子和棋盘棋子重合的次数的),递归直到它能等于你所设置的“#”数量即可。然后又退到上一层递归检查分支……这样不断循环….设置一个全局变量专门记录遍历能等于你所设棋子数量的次数即可。最后退出递归,输出这个全局变量的值。Ok ,问题得以解决!
代码说明如下,这个不要作为Acm提交用,方法较为麻烦,说明用,提交的话会超时:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define N 10
void search(int x, int y);
int columns[N];//记录第n列的状态,存在棋子且遍历过状态为1,否则为0
int num , fang_an ,area;//棋子数,方案数,行列数
char qipan[N][N];//设置字符串数组
int main(){
int j,i ;
while((scanf("%d%d",&area,&num))!=EOF){
while('\n'!=getchar());//输入完缓冲区会有换行符,后面
//要输入字符所以得清理缓冲区,本人惯用吃换行手段
if(area == -1 && num==-1 )break;
memset(qipan, 0 , sizeof(qipan));
for(i = 0; i < area ;i++ ){//输入字符串
scanf("%s",qipan[i]);
while('\n'!=getchar());
}
fang_an = 0;//将可行反案设置为0
memset(columns,0,sizeof(columns));//将记录行数的数组元素初始化0
search(0 ,0);//从坐标为(0,0)处开始走
printf("%d\n",fang_an);
}
}
void search(int x ,int y){
int i,j;
if(y == num ){//棋子数等于列数时,使方案递增,并退出当前层递归
fang_an++ ;
return ;
}
for( i = x ; i< area ; i++){
for( j = 0 ;j< area ; j++){
if((!columns[j]) && qipan[i][j] == '#'){//判断当前
//列是否已存在遍历过的棋子,并判断当前坐标中是否放的是棋子
columns[j] = 1;//若是的话,将当前列的状态改为1
search(x+1,y+1);
columns[j] = 0; //既然要退出了本层递归,就将本
//层行的状态改为初始状态
}
}
}
return ;
}
总结
一般来说,广搜常用于找单一的最短路线,或者是规模小的路径搜索,它的特点是”搜到就是最优解”, 而深搜用于找多个解或者是”步数已知(好比3步就必需达到前提)”的标题,它的空间效率高,然则找到的不必定是最优解,必需记实并完成全数搜索,故一般情况下,深搜需要很是高效的剪枝(优化).
像搜索最短路径这些的很显著是用广搜,因为广搜的特征就是一层一层往下搜的,保证当前搜到的都是最优解,当然,最短路径只是一方面的操作,像什么起码状态转换也是可以操作的。
深搜就是优先搜索一棵子树,然后是另一棵,它和广搜对比,有着内存需要相对较少的所长,八皇后标题就是典范楷模的操作,这类标题很显著是不能用广搜往解决的。或者像图论里面的找圈的算法,数的前序中序后序遍历等,都是深搜。
深搜的实现近似于栈,
广搜则是操作了队列,边进队,边出队。
优缺点:BFS:对于解决最短或最少问题特别有效,而且寻找深度小,但缺点是内存耗费量大(需要开大量的数组单元用来存储状态)。
DFS:对于解决遍历和求所有问题有效,对于问题搜索深度小的时候处理速度迅速,然而在深度很大的情况下效率不高
不管是BFS还是DFS,它们虽然好用,但由于时间和空间的局限性,以至于它们只能解决数据量小的问题。
题型归类
坐标类型搜索 :这种类型的搜索题目通常来说简单的比较简单,复杂的通常在边界的处理和情况的讨论方面会比较复杂,分析这类问题,我们首先要抓住题目的意思,看具体是怎么建立坐标系(特别重要),然后仔细分析到搜索的每一个阶段是如何通过条件转移到下一个阶段的。确定每一次递归(对于DFS)的回溯和深入条件,对于BFS,要注意每一次入队的条件同时注意判重。要牢牢把握目标状态是一个什么状态,在什么时候结束搜索。还有,DFS过程的参数如何设定,是带参数还是不带参数,带的话各个参数一定要保证能完全的表示一个状态,不会出现一个状态对应多个参数,而这一点对于BFS来说就稍简单些,只需要多设置些变量就可以了。
数值类型搜索:这种类型的搜索就需要仔细分析分析了,一般来说采用DFS,而且它的终止条件一般都是很明显的,难就难在对于过程的把握,过程的把握类似于坐标类型的搜索(判重、深入、枚举),注意这种类型的搜索通常还要用到剪枝优化,对于那些明显不符合要求的特殊状态我们一定要在之前就去掉它,否则它会像滚雪球一样越滚越大,浪费我们的时间 。
这次解题感觉很多地方并没有说清,若大神有疑问或发现一些bug,还请指正!!!