概念
鉴于普通二叉树使用过程中会出现空间的浪费,后人对在在二叉树的的基础上做了改进,利用它的空指针域存放在某种遍历次序下指向它的前驱结点,和后继结点的指针。这些指针称为线索,相应的二叉树就成了线索二叉树。
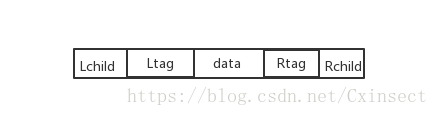
结点结构
- Ltag为0时指向该结点的左孩子,为1时指向该结点的前驱。
- Rtag为0时指向该结点的右孩子,为1时指向该结点的后继。
结构实现
线索存储结构定义
typedef enum {Link,Thread} PointerTag; //定义线索
typedef struct BithrNode{
char data; //结点数据
struct BithrNode *pLchild;
struct BithrNode *pRchild; //左右孩子
PointerTag Ltag;
PointerTag Rtag; //左右标志
}BiThrNode,*BiThrTree;树的线索化
树的线索化过程其实就是遍历过程中修改空指针域,因为此时当前结点的后继还没有访问到,只能对它的前驱结点进行判断,所以用一个全局变量来存储该结点的前驱结点,完成后续结点线索化。
BiThrTree pre; //定义全局变量,保存前驱结点中序遍历线索化过程
void InThreading(BiThrTree T)
{
if( T ) //判断根结点是否为空
{
InThreading(T->pLchild); //递归左子树线索
if (!T->pLchild) //左子树为空
{
T->Ltag = Thread; //前驱线索
T->pLchild = pre; //左子树保存前驱结点
}
if(!pre->pRchild) //右孩子为空
{
pre->Rtag = Thread; //后继线索
pre->pRchild = T; //右子树指向后继
}
pre = T; //保持pre指向T的前驱
InThreading(T->pRchild); //递归右子树线索化
}
return;
} 为了和双向链表一样,从根结点或者是尾结点都能访问整个树当中的数据,我们可以定义一个头结点,(a)让头结点的左指针域指向根结点,(b)右指针域指向中序遍历的最后一个结点。(c)让中序遍历的第一个结点的左指针域指向头结点,(d)最后一个结点的右指针域指向头结点。
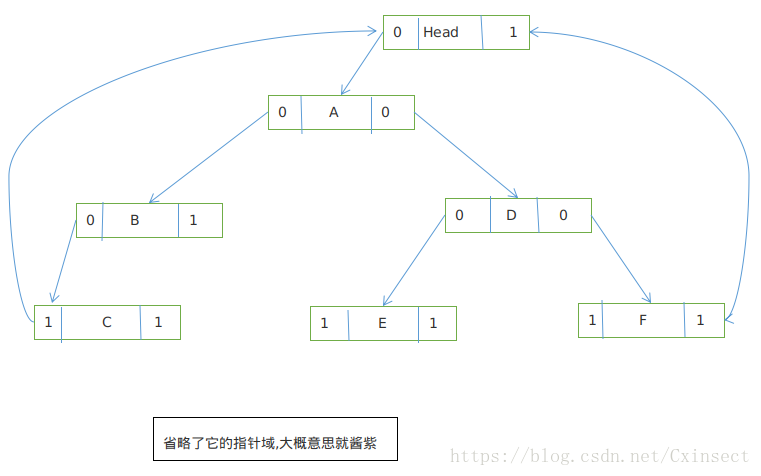
代码如下
- 其中p是头指针,t是根结点
void InOrdThreading(BiThrTree *p,BiThrTree t)
{
*p = (BiThrTree)malloc(sizeof(BiThrNode)); //为头结点分配空间
if((*p) == NULL)
{
printf("内存分配失败\n");
exit(1);
}
(*p)->Ltag = Link;
(*p)->Rtag = Thread; //后继线索线索
(*p)->pRchild = *p; //右指针域先指向自身
if(!t) //判断根结点是否为空
(*p)->pLchild = *p; //为空头结点左指针域指向自身
else{
(*p)->pLchild = t; //不空指向根结点
pre = *p; //初始化前驱结点
InThreading(t); //线索化过程
pre->pRchild = *p; //完成(b)过程
pre->Rtag = Thread; //后继线索化
(*p)->pRchild = pre; //完成(d)过程
}
return;
}遍历输出
- 其中p是头结点,T是根结点
void InOrderTraverse(BiThrTree p)
{
BiThrTree T;
T = p->pLchild;
while( p!=T) //空树或者遍历结束时
{
while(T->Ltag == Link) // 当Link等于0时循环到中序序列第一个结点
T = T->pLchild;
printf("%c\t",T->data); //打印数据
while(T->Rtag == Thread && T->pRchild != p)
{
T = T->pRchild;
printf("%c\t",T->data);
}
T = T->pRchild; //T递进至右子树根
}
printf("\n");
return;
} 输入
输出
树的建立采用前序遍历递归的方式创建,本篇文章不再赘述。
有问题欢迎指正。