写在前面:
大整数相加是很久之前写的,最近又写了大整数相乘,都不难,总结一下吧。
如果以后写了大整数相除也会补充进来的。
众所周知,int型的范围为:-2147483648 ~ +2147483647
long long in型的范围为:-9223372036854775808 ~ +9223372036854775807
在现在这个大数据横行的时代,有些非常大的数据根本不够。
所以我们需要进行数据很大的计算,简要思路就是:用字符串做运算。
大整数相加
大数相加是大数运算的基础,理解这个,理解其他就不难了。
我们在运算时,采用列竖式的方式,回忆一下,我们在小学时学习列竖式的时候:将个位与个位相加,大于10就进位,
再十位与十位相加,再进位。从低位开始,相同位数相加,多于10的进位,这就是基本思想。
就像这样:

我们不难发现,这种方法无疑就分为两步:
1.从最低位开始,先将同级位数对应相加。
2.判断是否需要定位,从低位开始往前一位进位。
(或者全部相加完再进位也可以)
相加这步很简单,而通过上面的例子我们发现进位也很简单,因为个位数和个位数相加是不超过20的,所以进位也就是说如果当前位数的值大于10,需要进位,便对10取余,然后前一位数加1便可。
我们通过代码来分析:
首先定义3个字符串数组,分别用来存储需要相加的两个值和最后结果,并对结果字符串初始化:
//#define N 200 //N自行设置
char a[N];
char b[N];
char s[N]; //结果数组
for(int i=0;i<N;i++) //初始化,一定要
{
s[i]=0;
}
cin>>a;
cin>>b;
然后就是将其从个位数字开始对应相加,因为要从个位数字开始,所以字符串要倒着开始遍历:
int la=strlen(a)-1,lb=strlen(b)-1;
int k=N-1;
while(la>=0 && lb>=0) //两个都还剩有数字
{
s[k]=s[k]+(b[lb--]-48)+(a[la--]-48); //两数相加,记得一定要减去48,因为是按字符数字存进去的
if(s[k]>=10) //进位设置
{
s[k]=s[k]%10;
s[k-1]++;
}
k--;
}
因为不能确定两个整数的总位数是否相等,所以需要判断看看是否加完了
if(la>=0 || lb>=0) //如果还有剩的
{
int x=max(la,lb);
for(int i=x;i>=0;i--)
{
if(la>=0) //如果还剩a字符串
{
s[k]=s[k]+(a[i]-48);
la--;
}
else //如果还剩b字符串
{
s[k]=s[k]+(b[i]-48);
lb--;
}
if(s[k]>=10) //进位
{
s[k]=s[k]%10;
s[k-1]++;
}
k--;
}
}
到这里计算过程就结束了,将其输出就可以了:
for(int i=1;i<N;i++) //输出
{
if(s[i]!=0) //当不为0时开始输出
{
for(int j=i;j<N;j++)
{
printf("%d",s[j]);
}
cout<<endl;
break;
}
}
单步代码很详细了,所以在这里就不列出完整代码了。
代码结果:
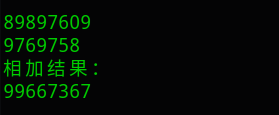
大整数相乘
相乘跟相加有共通之处也有不同之处,只要思路清晰,就很简单。
相乘也是列竖式法,
我们将被乘数的每一位,从低到高,依次乘以乘数的每一位,也是依次到高
最后对应每个位数,将其相加,再依次进位
不过因为char型字符串最大为128,而乘法每一位乘出来有可能会很大,加起来很有可能会超过这个值,更别说有的位数多,所以我们需要每次相加都进位。
如图所示:

初始化部分代码与上面相加部分相同,不做赘述。
因为乘法中,被乘数每一位都需要与乘数的每一位相乘,所以我们需要一个二维for循环:
int count=1,k;
int la=strlen(a),lb=strlen(b);
for(int i=lb-1;i>=0;i--) //二维for循环 ,i是被乘数
{
k=N-count; //因为乘法的进位,每次乘循环后,位数都要整体向前挪一位,count用来控制位数变化
for(int j=la-1;j>=0;j--) //j是乘数
{
s[k]=s[k]+((b[i]-48)*(a[j]-48)); //相加所乘的数
k--;
}
for(int l=N-count++;l>k-2;l--) //进位
{
if(s[l]<10) //如果小于10就不用进位
{
continue;
}
int m,n;
n=s[l];
s[l]=n%10;
m=n/10;
s[l-1]=s[l-1]+m; //进的位数加到前一位
}
}
输出部分也跟上述相加的部分相同,所以不做赘述。
代码结果:
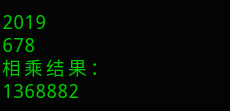
大整数相加和相乘相对来说比较简单,之后有时间看下大整数相除后会继续补充上来的。