最近看了看类的相关题，感觉简单的题过于模板，但是对于难题的转化，如果对与这方面的概念不清楚，很难写，故总结一下。
PS：博客里部分内容会和离散数学中的图论知识有联系，如果没有了解过相关知识可能比较难理解。
下文所说的割点=关节点，割边=桥=关节边。
首先声明一下，名叫Tarjan的算法有三种，分别为
（1） 有向图的强联通分量类问题
（2） 无向图的双联通分量（求割点，桥）类问题
（3） 最近公共祖先（LCA）
这里前两类问题比较相似，而第三类是解决LCA公共祖先问题的算法，这篇帖子将不会涉及。
下面我来具体解释一下各种概念
首先，先来理解一下连通图的概念
连通图，顾名思义，他所有的点应该都是连通的，这里的连通对于有向图和无向图来说还是有一定区别的。
无向图
在一个无向图G中，若从顶点i到顶点j有路径相连（当然从j到i也一定有路径），则称i和j是连通的。如果图中任意两点都是连通的，那么这个无向图就是连通图，简单来说只要他的所有节点都在一起连着，没有任何一个节点与其他节点直接没有连边，那么他就是一个连通图。
有向图
如果G是有向图，那么连接i和j的路径中所有的边都必须同向。如果图中任意两点都是连通的，则称为强连通图（注意：有向图需要双向都有路径，如果i可以到j而j不可以到i，那么就不是强连通图）。
有强连通图，就一定还会有弱连通图，将有向图的所有的有向边替换为无向边，所得到的图称为原图的基图。如果一个有向图的基图是连通图，则有向图是弱连通图。
简单理解就是，一个有向图，如果不是强连通图，把所有的边从无向看成有向，把有向图看成无向图，这时他如果变成了连通图，那么就说他是弱连通图。
上面在讲解有向图和无向图时引出了两个概念，强连通图和连通图，我先从无向图中的连通图来开始介绍
在无向图连通图的问题中，有两个概念非常重要，割点和桥，在大多数问题中都需要求这两个东西，在讲这两个东西之前，先来给大家介绍几个前置概念。
点连通度与边连通度 by kuangbin
在一个无向连通图中,如果有一个顶点集合,删除这个顶点集合,以及这个集合中所有顶点相关联的边以后,原图变成多个连通块,就称这个点集为割点集合。
一个图的点连通度的定义为,最小割点集合中的顶点数。
类似的,如果有一个边集合,删除这个边集合以后,原图变成多个连通块,就称这个点集为割边集合。
一个图的边连通度的定义为,最小割边集合中的边数。
简单总结：
点双连通：删掉一个点之后，图仍联通
边双连通：删掉一条边之后，图仍联通
双连通
定义：在无向连通图中，如果删除该图的任何一个结点或边都不能改变该图的连通性，则该图为双连通的无向图。，和点连通度与边连通度来结合这来说，就是点连通度或边连通度大于1的图。
ps：这部分概念理解知道就好，对于做题来说帮助不是很大。
双连通图割点与桥 by kuangbin
如果一个无向连通图的点连通度大于 1,则称该图是点双连通的 (point biconnected),简称双连通或重连通。一个图有割点,当且仅当这个图的点连通度为 1,则割点集合的唯一元素
被称为割点 (cut point),又叫关节点 (articulation point)。
这里割点的概念就出来了，大概意思就是，如果连通图里有一个点，把这个点和他所连接的边删掉，那么他就不连通了，那么这个点就叫做割点，下图标红的点就是割点。
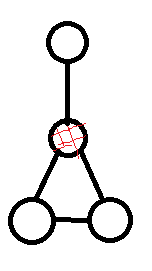（图源自网络，侵删）
理解了割点，那么理解割边也就很容易了
如果一个无向连通图的边连通度大于 1,则称该图是边双连通的 (edge biconnected),简称双
连通或重连通。一个图有桥,当且仅当这个图的边连通度为 1,则割边集合的唯一元素被称为桥 (bridge),又叫关节边 (articulation edge)。
下图标红的边就是割边。
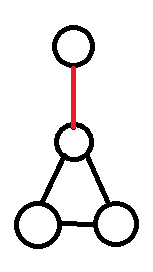图源自网络，侵删）
可以看出,点双连通与边双连通都可以简称为双连通,它们之间是有着某种联系的,下文中提到的双连通,均既可指点双连通,又可指边双连通。
PS：而如果有桥，这个图必有割点，如果有割点，不一定会有桥，这个很好证明，看看图就知道了。
总结：若一个无向图中的去掉任意一个节点（一条边）都不会改变此图的连通性，即不存在割点（桥），则称作点（边）双连通图。
相信看过上面如此详细的概念，大家对割点和割边已经有了深刻的认识了，那么这里就给大家求割点和割边的两道入门题，学习如何用求tarjan算法求割点割边，可以在啊哈算法中看相应章节，个人感觉是市面上能找到资料里写的最好的了。
luogu P3388 【模板】割点（割顶）
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
vector<int> g[20010];
int dfn[20010],low[20010],iscut[20010],son[20010];
int deep,root,n,m,ans;
int tarjan(int u,int fa)
{
int child=0,lowu;
lowu=dfn[u]=++deep;
int sz=g[u].size();
for(int i=0;i<sz;i++)
{
int v=g[u][i];
if(!dfn[v])
{
child++;
int lowv=tarjan(v,u);
lowu=min(lowu,lowv);
if(lowv>dfn[u])
{
iscut[u]=1;
}
}
else
{
if(v!=fa&&dfn[v]<dfn[u])
{
lowu=min(lowu,dfn[v]);
}
}
}
if(fa<0&&child==1)
{
iscut[u]=false;
}
low[u]=lowu;
return lowu;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++){
int from,to;
scanf("%d%d",&from,&to);
g[from].push_back(to);
g[to].push_back(from);
}
for(int i=1;i<=n;i++){
if(!dfn[i]){
root=i;
tarjan(i,-1);
}
}
for(int i=1;i<=n;i++){
if(iscut[i]){
ans++;
}
}
printf("%d\n",ans);
for(int i=1;i<=n;i++){
if(iscut[i]){
printf("%d ",i);
}
}
}
luogu P1656 炸铁路（割边）
#include<cstdio>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
vector<pair<int,int>>bridge;
vector<int> g[10010];
int dfn[10010],low[10010];
int deep,root,n,m,ans;
bool cmp(pair<int,int> a,pair<int,int> b){
if(a.first == b.first)
return a.second < b.second;
else
return a.first < b.first;
}
int tarjan(int u,int fa)
{
int lowu;
lowu=dfn[u]=++deep;
int sz=g[u].size();
for(int i=0;i<sz;i++)
{
int v=g[u][i];
if(!dfn[v])
{
int lowv=tarjan(v,u);
lowu=min(lowu,lowv);
if(lowv>dfn[u])
{
int from,to;
from=u;
to=v;
if(from>to)
{
swap(from,to);
}
bridge.push_back(make_pair(from,to));
}
}
else
{
if(v!=fa&&dfn[v]<dfn[u])
{
lowu=min(lowu,dfn[v]);
}
}
}
low[u]=lowu;
return lowu;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int from,to;
scanf("%d%d",&from,&to);
g[from].push_back(to);
g[to].push_back(from);
}
for(int i=1;i<=n;i++)
{
if(!dfn[i])
{
root=i;
tarjan(i,-1);
}
}
sort(bridge.begin(),bridge.end(),cmp);
for(int i=0;i<bridge.size();i++)
{
printf("%d %d\n",bridge[i].first,bridge[i].second);
}
}
好，现在这一阶段结束了，我们进行下一阶段的概念理解
双连通分量
先来看一看kuangbin的解释，个人感觉不是很好理解，所以下面还有一种比较简单易懂的解释。
在图 G 的所有子图 G’ 中,如果 G’ 是双连通的,则称 G’ 为双连通子图。如果一个双连通子
图 G’ 它不是任何一个双连通子图的真子集,则 G’ 为极大双连通子图。双连通分支
(biconnected component),或重连通分支,就是图的极大双连通子图。特殊的,点双连通分
支又叫做块。
双连通分量分为边双连通分量和点双连通分量两种。
一个无向图中的每一个极大点（边）双连通子图称作此无向图的点（边）双连通分量。
边双连通分量
边双连通分量：在分量内的任意两个点总可以找到两条边不相同的路径互相到达。总而言之就是一个圈，正着走反着走都可以相互到达，至少只有一个点。也就是同一边双内，点与点的边集中无桥，注意割边不属于任何一个边双联通分量。
简单的说，就是一个无向图，减去他们所有的割边，剩下个各个部分，就是各个边连通分量，如下两张图所示，红边为割边，删掉以后，剩下的三个子图就是三个边连通分量（图源网络，侵删）
删掉之后
边双联通分量求法模板
边双联通分量的求解关键点在于桥。如果遇到一个桥的时候就说明有两个边双联通分量。
poj 3177 Redundant Paths(边双连通分量+缩点) 来自这篇帖子
#include<cstdio>
#include<cstring>
const int N=5000+5;
const int M=10000+5;
struct EDGE
{
int v,next;
}edge[M*2];
int first[N],low[N],dfn[N],belong[N],degree[N],sta[M],instack[M];
int g,cnt,top,scc;
int min(int a,int b)
{
return a<b?a:b;
}
void AddEdge(int u,int v)
{
edge[g].v=v;
edge[g].next=first[u];
first[u]=g++;
}
void Tarjan(int u,int fa)
{
int i,v;
low[u]=dfn[u]=++cnt;
sta[++top]=u;
instack[u]=1;
for(i=first[u];i!=-1;i=edge[i].next)
{
v=edge[i].v;
if(i==(fa^1))
continue;
if(!dfn[v])
{
Tarjan(v,i);
low[u]=min(low[u],low[v]);
}
else if(instack[v])
low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u])
{
scc++;
while(1)
{
v=sta[top--];
instack[v]=0;
belong[v]=scc;
if(v==u)
break;
}
}
}
int main()
{
int n,m,u,v,i,j;
scanf("%d%d",&n,&m);
g=cnt=top=scc=0;
memset(first,-1,sizeof(first));
memset(low,0,sizeof(low));
memset(dfn,0,sizeof(dfn));
memset(instack,0,sizeof(instack));
memset(degree,0,sizeof(degree));
for(i=0;i<m;i++)
{
scanf("%d%d",&u,&v);
{
AddEdge(u,v);
AddEdge(v,u);
}
}
for(i=1;i<=n;i++)
if(!dfn[i])
Tarjan(1,-1);
for(i=1;i<=n;i++)
{
for(j=first[i];j!=-1;j=edge[j].next)
{
v=edge[j].v;
if(belong[i]!=belong[v])
degree[belong[i]]++;
}
}
int sum=0;
for(i=1;i<=n;i++)
if(degree[i]==1)
sum++;
int ans=(sum+1)/2;
printf("%d\n",ans);
return 0;
}
点连通双分量
点双连通分量：至少为一个点。对于同属一个点双的任意点，删除后，该分量中的点仍能互相到达；或者说仅对于该分量而言，无割点。
由于割点将原图分成互不相连的多个联通块，显然每个联通块本身已经是一个点双了，但不完整，因为相邻的割点在边界，如果与联通块共同组成一个新联通块，割掉后也不会另外产生联通块(相当于该连通块上的叶子节点)，所以需要加上割点来才完整(故割点会同时出现在多个点双联通分量中)。但注意，非割点只会出现在一个点连通分量中（图源网络，侵删）
原图
其中一个点双连分量
与上面那个点连通分量同割点的另一个点连通分量
点双联通分量的求解关键点在于割点。
点双联通分量求法模板
该模板可求，遇见题可根据相求的点进行求解。
点连通分量个数：num
每个点连通分量的个数：bccnum[i]
求解完点连通分量之后的结果：bcc
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int mod = 998244353;//取模
const int maxn = 3e5+10;//点的数量
const int maxm = 10e5+10;//边的数量,注意双向边要弄两倍的
struct edge
{
int to,pre;
}edges[maxm];//邻接表
int head[maxn],dfn[maxn],dfs_clock,tot;
LL num;//BCC数量
int Stack[maxn],Top;//模拟栈
vector<int>bcc[maxn];//缩点之后的图
int bccnum[maxn];//存每个合点中包含点的数量
inline int Min(int a,int b){
if(a>b)return b;
else return a;
}//注意min是自己写的
/* inline LL qpow(LL x) { */
/* LL res = 1, temp = 2; */
/* while (x) { */
/* if (x & 1) { */
/* res = (res * temp) % mod; */
/* } */
/* temp = (temp * temp) % mod; */
/* x >>= 1; */
/* } */
/* return res % mod; */
/* } */
int tarjan(int u,int fa)
{
int lowu=dfn[u]=++dfs_clock;
for(int i=head[u];i;i=edges[i].pre)
if(!dfn[edges[i].to])
{
Stack[++Top]=edges[i].to;//搜索到的点入栈
int lowv=tarjan(edges[i].to,u);
lowu=Min(lowu,lowv);
if(lowv>=dfn[u])//是割点或根
{
num++;
while(Stack[Top]!=edges[i].to){
/* Top--; */
bcc[num].push_back(Stack[Top--]);//图
bccnum[num]++;//点的加法
}
/* Top--; */
bccnum[num]++;
bccnum[num]++;
bcc[num].push_back(Stack[Top--]);//目标点出栈
bcc[num].push_back(u);//不要忘了将当前点存入bcc
}
}
else if(edges[i].to!=fa)
lowu=Min(lowu,dfn[edges[i].to]);
return lowu;
}
inline void add(int x,int y)//邻接表存边
{
edges[++tot].to=y;
edges[tot].pre=head[x];
head[x]=tot;
}
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
add(x,y),add(y,x);
}
for(int i=1;i<=n;i++)//遍历n个点tarjan
if(!dfn[i])
{
Stack[Top=1]=i;
tarjan(i,i);
}
for(int i=1;i<=num;i++)
{
printf("BCC#%d: \n",i);
printf("该分量点的个数：%d\n",bccnum[i]);
printf("分别包含哪一个点：\n");
for(size_t j=0;j<bcc[i].size();j++){
printf("%d ",bcc[i][j]);
}
printf("\n");
}
return 0;
}
【双连通分量常见的模型和问法】
1.给出的图是非连通图，如：
a.有一些点，一些边，加最少的边，要使得整个图变成双联通图。
大致方法：求出所有分量，把每个分量看成一个点，统计每个点的度，有一个度为一则cnt加1，答案为（cnt+1）/2；
b.有一些点，一些边，问最少多少个点单着。
大致方法：求出所有的分量即可，但要注意不同的题可能有特殊要求（如圆桌骑士要求奇圈，要用到二分图判定）
c.各种变式问题
2.给出的图是连通图，如：
a.给定一个起点一个终点，求各种问题是否能实现。
大致方法：求出所有分量，并把每个分量当成点，于是问题得到化简；
b.给一个图，然后有大量的离线回答。
大致方法：求出所有分量，再求出上下子树的信息；
c.各种变式问题；
无向图基本介绍完了，现在在来介绍介绍有向图的相关概念。
强连通图
就像上面说过的，强连通是指一个有向图中任意两点v1、v2间存在v1到v2的路径及v2到v1的路径，同样，有向图也有强连通分量的这一说法。
强连通分量
在强连通图的基础上加入一些点和路径，使得当前的图不在强连通，称原来的强连通的部分为强连通分量。 与上面两种类似，强连通分量也至少为一个点。
缩点
同属一个强连通分量的点，互相之间可以互相到达，所以他们在很多问题中可以看成是一个点，把整个图里每个强连通分量看成一个点的过程就叫做缩点，之后在建一个新图，该图就一定是有向无环图了，便可以解决很多在缩点之前难以解决的问题，建议可以去找板子题做一做。
强连通分量问题模板
我借这道题，把强连通分量几乎会出到的所有模板，都写在这道题的模板里面，做题时只需要选择自己需要的自行使用
tarjan求强连通分量并缩点建图+dag有向无环图的dp问题去求解最大值 洛谷p3387
#include <stdio.h>
#include <string.h>
#include <vector>
#include <stack>
#include <iostream>
#define repu(i,a,b) for(int i=a;i<b;i++)
using namespace std;
#define N 10005 /// 题目中可能的最大点数
stack<int>sta; /// 存储已遍历的结点
vector<int>gra[N]; /// 邻接表表示图
int dfn[N]; /// 深度优先搜索访问次序
int low[N]; /// 能追溯到的最早的次序
int InStack[N]; // 检查是否在栈中(2：在栈中，1：已访问，且不在栈中，0：不在)
vector<int> Component[N]; /// 获得强连通分量结果
int InComponent[N]; /// 记录每个点在第几号强连通分量里
int Index,ComponentNumber;/// 索引号，强连通分量个数
int n,m; // 点数，边数
int chu[N]; //出度
int dianquan[N]; //初始图点权
int dianquan2[N]; //缩点后点权
int dp[N]; //dag缩点时
int vis[N];
int ru[N]; //入度
int num[N]; //各个强连通分量包含点的个数,数组编号 1 ∼ scc
void init() //清空容器，数组
{
memset(dp, 0, sizeof(dp));
memset(vis, 0, sizeof(vis));
memset(dianquan2, 0, sizeof(dianquan2));
memset(dianquan ,0, sizeof(dianquan));
memset(dfn, 0, sizeof(dfn));
memset(low, 0, sizeof(low));
memset(chu, 0, sizeof(chu));
memset(InStack, 0, sizeof(InStack));
Index = ComponentNumber = 0;
for (int i = 1; i <= n; ++ i)
{
gra[i].clear();
Component[i].clear();
}
while(!sta.empty())
sta.pop();
}
void tarjan(int u)
{
InStack[u] = 2;
low[u] = dfn[u] = ++ Index;
sta.push(u);///寻找u所在的强连通分量
for (size_t i = 0; i < gra[u].size(); ++ i)
{
int t = gra[u][i];
if (dfn[t] == 0)///不在的继续递归
{
tarjan(t);///递归到头了就
low[u] = min(low[u], low[t]);
}
else if (InStack[t] == 2)///在栈里
{
low[u] = min(low[u], dfn[t]);
}
}
if(low[u] == dfn[u])///sta出栈就是一个强连通分量的
{
++ComponentNumber;///强连通分量个数
while (!sta.empty())
{
int j = sta.top();
sta.pop();
InStack[j] = 1;///已访问但不在栈中
InComponent[j]=ComponentNumber;
dianquan2[ComponentNumber]+=dianquan[j];
///记录每个点在第几号强连通分量里
num[ComponentNumber]++;
if (j == u)
break;
}
}
}
void input()
{
int x,y;
scanf("%d%d",&n,&m);
repu(i,1,n+1)
{
scanf("%d",&dianquan[i]);
}
repu(i,1,m+1)
{
scanf("%d%d",&x,&y);
gra[x].push_back(y);///有向图才有强连通分量
}
}
int dfs(int u){
if(dp[u]){
return dp[u];
}
else{
dp[u] = dianquan2[u];
for(size_t i = 0;i < Component[u].size();i++){
int y = Component[u][i];
dp[u] = max(dp[u],dfs(y)+dianquan2[u]);
}
return dp[u];
}
}
void solve()
{
for(int i=1; i<=n; i++)
if(!dfn[i])
tarjan(i);
//缩点
for(int i = 1;i <= n;i++){
for(size_t j = 0;j < gra[i].size();j++){
if(InComponent[i] != InComponent[gra[i][j]]){
//chu[InComponent[i]]++;//求出度
//ru[InComponent[gra[i][j]]]++;//求入度
Component[InComponent[gra[i][j]]].push_back(InComponent[i]); //缩点建图
}
}
}
int aans = 0;
for(int i = 1;i <= ComponentNumber;i++){
memset(dp,0,sizeof(dp));
aans = max(dfs(i),aans);
/* printf("%d ",dianquan2[i]); */
}
printf("%d\n",aans);
}
int main()
{
init();
input();
solve();
return 0;
}
【强连通分量常见的模型和问法】
1.给出的是非连通图，如：
a.有一些点，一些有向边，求至少加多少边使任意两个点可相互到达
大致方法：求出所有的分量，缩点，分别求出出度入度为0的点的数量，取多的为答案；
b.有一些点，一些有向边，求在这个图上走一条路最多可以经过多少个点
大致方法：求出所有的分量，缩点，形成一个或多个DAG图，然后做DAG上的dp
c.有一些点，一些有向边，给出一些特殊点，求终点是特殊点的最长的一条路
大致方法：求出所有分量，并标记哪些分量有特殊点，然后也是DAG的dp
2.给出的是连通图，比较少，有也比较简单
总结：
1.遇到非连通图几乎可以肯定是要求连通分量，不论是无向还是有向图；（可以节约大量思考时间）
2.凡是对边、点的操作，在同一个分量内任意一个点效果相同的，几乎都是缩点解决问题；再粗暴点，几乎求了连通分量都要缩点；
3.一定要考虑特殊情况，如整个图是一个连通分量等。
4.对于双连通分量要分析是边还是点双连通分量；通过题目来判断；
5.拿到题目要先搞清楚给的是连通图还是非连通图。
这篇文章有部分是借鉴其他一些博客的内容，链接我放在下面，这篇帖子在算法具体实现上讲解的更加细化，更加适合入门看看。
基本图论-连通分量(强/弱联通 割点/边 边/点双)
tarjan求强连通分量+缩点+割点/割桥（点双/边双）以及一些证明