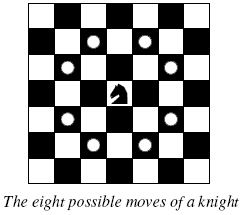
整天待在一个方块里, 骑士感到特别的无聊, 于是, 他决定来一场所走就走的旅行但他只能走日字, 并且世界是一个不大于88的棋盘.你能帮勇敢的骑士制定一个旅行计划吗?请找出一条路使得骑士能够走遍整个棋盘.骑士可以在任一方块出发或结束
输入
第一行输入一个正整数n, 代表数据组数对于每组数据, 含有两个正整数p和q(1 <= pq <= 26), 表示一个p*q的棋盘.每个方块的位置用两个字符表示, 第一个从A开始,代表列, 第二个从1开始,代表行
输出
每组数据的结果首先是一行"Scenario #i:", i是数据序号, 从1开始然后输出一行, 是字典序第一的可以走遍棋盘的路径, 接着有一个空行路径应该是连续的依次所走方块的位置如果不存在这样的路径, 输出"impossible"
Sample Input3
1 1
2 3
4 3Sample OutputScenario #1:
A1
Scenario #2:
impossible
Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4
理解:对于这道题 肯定是要用DFS来做的 我们要注意的问题有两点:
- 首先我们要注意的是回溯的问题 深搜和树的前序遍历很相似 以树来想 有可能已经到了左边的叶结点还有元素没有搜索到 不难明白我们需要回溯
- 对于每次DFS执行的判断条件 因为有可能我们已经遍历了所有的元素 我们需要从前面已经建立的类似栈的结构中一点一点跳出 所以除了一般的条件 我们还需要加上一点 我的代码中是设置了一个bool型的变量 用这个变量的值来去当作判断条件
大概实现思路:
使用了一个结构体数组去储存行与列的下标 使用一个bool型变量来判断是否遍历完所有的元素 再就是上面所说的回溯与判断条件
下面是这道题的AC代码:`
//AC
#include<stdio.h>
#include<string.h>
int dx[8] = {-1, 1, -2, 2, -2, 2, -1, 1};
int dy[8] = {-2, -2, -1, -1, 1, 1, 2, 2};
int a[15][15];
int sum,m,n,ans=1;//ans为步数
bool judge;
struct code
{
int col; //行
int row; //列
} tmp[70];
void dfs(int x,int y,int ans)
{
tmp[ans].row=x;
tmp[ans].col=y;
if(ans==m*n)
{
judge=true;
return;
}
for(int i=0;i<8;i++)
{
int nx=x+dx[i];
int ny=y+dy[i];
if(nx>=1 && nx<=m && ny>=1 && ny<=n && a[nx][ny]==0 && !judge)
{
a[nx][ny]=1;
dfs(nx,ny,ans+1);
a[nx][ny]=0; //很巧妙的一种回溯方法
} //在没有路的可以走的时候开始回溯
}
}
int main()
{
int i,j,k;
scanf("%d",&sum);
for(i=0;i<sum;i++)
{
judge=0; //第一次这里出现错误
memset(a,0,sizeof(a));
scanf("%d %d",&m,&n);
a[1][1]=1;
dfs(1,1,1); //步数在这里每一个循环被初始化
printf("Scenario #%d:\n",i+1);
if(judge)
for(int j=1;j<=m*n;j++)
printf("%c%d",tmp[j].col+'A'-1,tmp[j].row);
else
printf("impossible");
printf("\n");
if(i!=sum-1)
printf("\n");
}
return 0;
}