贪心算法(英语:greedy algorithm),又称贪婪算法,是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的算法 —维基百科
贪心是一种解决问题的策略.如果策略正确,那么贪心法往往是易于描述,易于实现的. —刘汝佳
题目类型 :
1. 最优装载问题
2. 部分背包问题
3. 乘船问题
4. 选择不相交区间
5. 区间选点问题
6. 区间覆盖问题
7.任务调度问题
8.Huffman编码
由于 Huffman编码我暂时也搞的也不是很清楚 就不 班门弄斧 了 ,如果想看Huffman 可以先走了,不用耽误时间了.搞清楚之后,在更新
最优装载问题
题干 : 给出n个物体,第 i 个物体重量为 wi,选择尽量多 的物体,使得总重量不超过 c
由于只关心个数,而忽略重量 .
策略 : 每次选当先剩下物体中重量最小的物体,在 c 的范围内 .
部分背包问题
题干 : 有 n 个物体,第 i 个物体的重量为 wi,价值为 vi.在总重量不超过 c 的情况下让总价值尽量高,每一个物体都可以只取走一部分,价值和重量按比例计算.
这类题型 ,选择重点就是 我们经常所说的 性价比
策略 : 每次所选的 是剩下物体里面 性价比 最高的物体.当背包装不下 整个物体时,可以按照 百分比 选择其中的一部分
乘船问题
题干 : 有 n 个人,第 i 个人重量 为wi,美艘 船的最大载重量均为 c ,且最多只能乘 2 个人,用最少的船装载所有人.
由于所求的是 用最少的船装载 ,所以每次尽量 让 2 个人 同时乘船 当 船的重量允许时.
策略 : 在船的载重量的范围内 ,每次选择时, 让当前所有人中 最轻 的 当前所有人中最重 的人乘坐 一艘船,这样就会使船 的载重量 浪费最少.
当最轻的人 无法和 船上的任意 一人同坐一艘船时,剩下的所有人 都只能一人坐一艘船了 .
因为 当最轻的人都无法 和 别人一起乘坐时 ,再剩下的所有人中,任意两人 的重量 都大于 最轻的人和另一个人的重量,所以只能一人乘坐一艘船了
选择不相交区间
题干 : 数轴上有n 个开区间(ai,bi).选择尽量多个区间,使得这些区间两两没有公共点.
按照 bi从小到大的顺序给区间排序
策略 :每次选择的是目前不相交区间里的第一个区间.
原因
当 a1 == a2 时
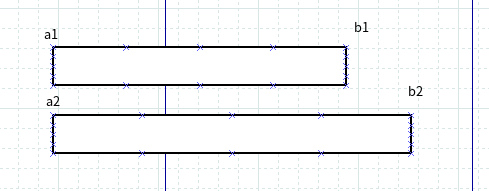
因为 要选择尽量多的区间,所以浪费的区间越小,其他的区间能利用的空间就越大,很明显 选择是第一个
当 a1 > a2 时
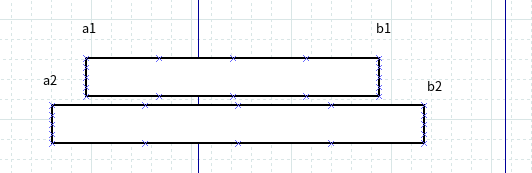
同上, 当在这 所浪费的空间只有 b2 - b1,而 a1 - a2 的空间不算浪费 ,想想为什么
当 a1 < a2 时
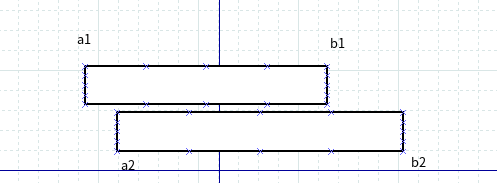
因为 每选择一个区间 后,这个区间 的 起始端 到 它前面 一个区间的 末端 这块 区间 是无法利用的,也就是 b0 到 a1这块区间是利用不到的,减少浪费 是因为 为了后面的区间 能利用上这块区间,当利用不 上的时候 节省 也就没有了意义.
换句话来讲,每次选择的 是 剩下区间 里 bi 最小的一个.当然在不相交的前提下.

#include<iostream>
#include<algorithm>
using namespace std;
struct node
{
int start;
int end;
};
struct node a[105];
int cmp(struct node a,struct node b)
{
return a.end < b.end;
}
int main( )
{
int n;
while(cin >> n && n != 0)
{
for(int i = 1;i <= n;i++) cin >> a[i].start >> a[i].end;
sort(a+1,a+n+1,cmp);
int cnt = 1;
int temp = a[1].end;
for(int i = 2;i <= n;i++)
{
if(temp <= a[i].start)
{
cnt++;
temp = a[i].end;
}
}
cout << cnt << endl;
}
}
区间选点问题
题干 : 数轴上有 n 个闭区间[ai,bi],取尽量少的点,使得每个 区间内 至少有一个点(不同区间含的点 可以是 同一个)
按照 b 从小到大 排序
策略 : 每次选取 当前区间的最后 一个点
原因

如上图 : 如果区间选择 了 (a1,b1) 时,只有在点 D 是,才是最正确的点.也是 目前 最好的选择
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
struct node
{
double start;
double end;
};
struct node a[1005];
int cmp(struct node a,struct node b)
{
if(a.end != b.end) return a.end < b.end;
else return a.start > b.start;
}
int main( )
{
int n,radius;
double tempx,tempy;
int flag;
int num = 1;
while(cin >> n >> radius && n != 0)
{
flag = 0;
for(int i = 1;i <= n;i++)
{
cin >> tempx >> tempy;
if(tempy > radius) flag = 1;
a[i].start = tempx - sqrt((radius * radius *1.0) - (tempy * tempy*1.0));
a[i].end = tempx + sqrt((radius * radius *1.0) - (tempy * tempy*1.0));
}
if(flag == 1)
{
cout << "Case " << num << ": -1" << endl;
num++;
continue;
}
sort(a+1,a+n+1,cmp);
int cnt = 1;
double temp = a[1].end;
for(int i = 2;i <= n;i++)
{
if(a[i].start <= temp) continue;
else
{
cnt++;
temp = a[i].end;
}
}
cout << "Case " << num << ": " << cnt << endl;
num++;
}
return 0;
}
区间覆盖问题
数轴上有n 个闭区间[ai,bi],选择 尽量少的区间覆盖一条指定线段[s,t]
把各区间按照 ai 从小到大排序
策略 : 如果只有一个起点,就选择这个起点,如果是多个起点则 在每次起点 上的 所有区间里 选择 最长的区间.(也就是 bi 最大的区间)

若,起点为 a1,那当然 只能选择 (a1,b1)区间了,若起点 为 A ,则选择的是 区间(a2,b2).因为 相同的起点,当然 b2 越长,所选择的 区间就越少了.
这类题思想简单,实现 时 就稍微 困难点.
Minimal coverage
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
struct node
{
int start;
int end;
};
struct node a[100005];
int book[100005];
int cmp(struct node a,struct node b)
{
return a.start < b.start;
}
int main( )
{
int T;
cin >> T;
while(T--)
{
memset(book,0,sizeof(book));
int len;
cin >> len;
int i = 1;
int tempstart,tempend;
while(cin >> tempstart >> tempend && (tempstart || tempend))
{
if(tempend <= 0 || tempstart >= len) continue;
a[i].start = tempstart;
a[i].end = tempend;
i++;
}
sort(a+1,a+i,cmp);
if(a[1].start > 0)
{
cout << 0 << endl;
continue;
}
int temp = 0,tempmax = 0,coordinate;
int t = -1; //用来备份起点相同 的上一个 区间
for(int j = 1;j < i;j++)
{
if(a[j].start <= temp)
{
if(a[j].end > tempmax)
{
book[j] = 1;
if(t != -1) book[t] = 0;
tempmax = a[j].end;
t = j;
}
}
else
{
temp = tempmax;
t = -1;
j--;
}
if(tempmax >= len) break;
}
if(tempmax < len)
{
cout << 0 << endl;
continue;
}
int cnt = 0;
for(int j = 1;j < i;j++) if(book[j]) cnt++;
cout << cnt << endl;
for(int j = 1;j < i;j++)
{
if(book[j])
{
cout << a[j].start << " " << a[j].end << endl;
}
}
}
return 0;
}
任务调度问题
题干 : 给定 n 向任务,每项任务的开始时间 为si,结束时间为ei,(1 <= i <= n,0<= si< ei),且没想任务只能在一台机器上完成每台机器一次只能完成一项任务.如果任务 i 和任务 j 满足 ei <= sj 或 ej < si.则任务 i 和 任务 j 是不冲突的,可以在一台机器上完成
对每项任务开始时间 升序进行排序
最少用的机器台数为 m = 0
策略 : 每次选择当前最小开始时间的任务
if(任务 i 和已经执行的任务不冲突) 安排任务 i 在空闲的机器上完成
else
{
m++; //添加一台新机器
任务 i 在新机器完成
}
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
typedef pair<int ,int> pii;//时间点,前一个表示时间点的是兼职,后一个表示这个时间点是开始时间还是结束时间
const int N = 1e5 + 10;
pii a[2*N]; //2n 个时间点
int l[N],r[N]; //l 记录机器的开机时间 ,r 机器的关机时间
int main()
{
int t;
long long sum = 0;
scanf( "%d",&t);
while(t--)
{
int n;//一共n 项任务
scanf( "%d",&n);
for(int i = 1;i <= n;i++)
{
int left,right;
scanf("%d%d",&left,&right);
a[2*i - 1] = pii(left,1);
a[2*i] = pii(right,-1);
}
sort(a+1,a+2*n+1);
memset(l,-1,sizeof(l));
memset(r,-1,sizeof(r));
int num = 0,ans = 0; //num 表示当前运行的机器数量 ans 表示到当前一共开过多少台机器
for(int i = 1;i <= 2*n;i++)
{
if(a[i].second == 1)
{
num++;
if(l[num] == -1) l[num] = r[num] = a[i].first;//num 是新开的机器
ans = max(ans,num);
}
else
{
r[num] = a[i].first;
num--;
}
}
sum = 0;
for(int i = 1;i <= ans;i++)
{
sum +=(r[i] - l[i]);
}
cout << ans << " " << sum << endl;
}
}