本篇博客是来讲解一下AVL树的实现过程~~~
文章目录
前言
一、平衡二叉树是什么?
解释:平衡二叉树是带有平衡条件的二叉查找树,也称为平衡二叉树。能被称为平衡二叉树的要求是每个节点的左子树和右子树的高度差的绝对值不能大于1。
想想:二叉查找树对于查找可以说是提升了很大的效率,那为什么还要出现一个平衡二叉,任何事物的出现都有他存在的理由,所以我们先来看一下二叉查找树和平衡二叉树的区别,或者说平衡二叉树他比二叉查找树好在哪里。
看如下两棵树:
图1 普通的二叉查找树
图2 AVL树
比较图一和图二当我们查找 D的时候,很明显图2要比图1查找的效率更高。
我们知道当一颗二叉查找树平衡的时候,该树的平均查找长度为O(Log2^n),近似于折半查找。如果二叉排序树完全不平衡,如上图,则其深度可达到n,那么他的查找效率就退化为为O(n)了,退化为顺序查找。一般的,二叉排序树的查找性能在O(Log2^n)到O(n)之间。因此,为了获得较好的查找性能,就要构造一棵平衡的二叉排序树,也就是我们今天的主角“平衡二叉树(图2)”
如过有同学不会计算平均查找长度的话可以看下面的介绍,会的话就可以直接跳过这部分看下面了。
1.平均查找长度的计算
在查找这一部分,我们暂且称时间复杂度为平均查找长度,那莫如何来计算呢?
我们先来了解一个公式
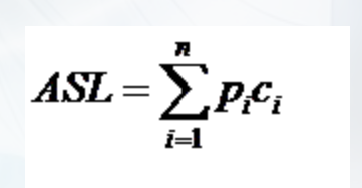
其中ASL是平均查找长度的缩写,Pi代表的是查找第i个元素的概率,通常假设每个元素查找概率相同,Pi=1/n,n为元素的个数,Ci是找到第i个元素的比较次数。
了解了ASL的相关概念,接下来我们就小练一下
我们可以了解到,第一层查找次数为1,第二层为2,.....所以根据上面的ASL的计算公式得出"查找成功"的平均查找长度为(1*1+2*2+2*3+4*1)/ 6 "查找不成功的为"=(2*3+3*4+5*2)/ 7
查找成功很好理解,那为什莫查找不成功这么算呢,假设我们找到了某个想要找到的值,那莫在内部结点就能查找成功,而查找不成功的就是那些空的外部结点,所以一样的道理只是结点换成了那些空的,但是这些空的结点实际是不存在的,只是为了计算查找不成功来专门标注的让大家来理解的。
了解了平均查找长度的计算相信大家对于平衡二叉树和普通的二叉查找树的执行效率也有了更好的理解,同学们可以自己下去找一组数据,分别写出他的普通方式和平衡方式然算一下他的平均查找长度,就能更好地看出那个效率更高了。那莫接下来就让我们进入平衡二叉树的世界吧。
如何构建一个颗平衡二叉树树呢?如下~
二、构建平衡二叉树
1.单旋(LL型)
依次插入3 2 1 同时进行右旋

我们可以看见当依次加入 3 2 时每个结点都是平衡的,当加入1的时候,就出现了不平衡的结点 3,那莫我们就要进行旋转将这个结点变成平衡的,也就是上面的操作,称为LL型(右旋)
2.单旋(RR型)
依次插入1 2 3同时进行左旋

依次插入时,构成不平衡的结点为1 这是我们将他左旋 称为(RR型)
3.双旋(RL型)
依次插入1 3 2 先进行LL型在RR型

双旋看起来就比单旋稍微复杂一点要先进行LL型的旋转在进行RR型的旋转,这样就平衡了。
4.双旋(LR型)

和上面的描述类似。
练习
了解旋转的四种状态,那笔者就出一点稍微复杂的旋转了,可没上面那麽简单了呦。

是不是感觉比起前面的有点难度了呢,接下来我们就来法分析一下这个是如何生成的呢,这棵树变得有难度了就是因为他的有些结点有了子树,你可能不知道他应该放在哪,他就让我们来一探究竟吧。首先我们可以看到发生不平衡的节点为8,我们发现左子树比右子树的高度高。初步判定为以L~型的,然后顺着左边的第一个节点来看发现这个节点的右子树比左子树高,那莫这下我们就可定义为LR型旋转了,想一想LR型旋转怎莫转呢,先进行RR旋转 也就是上面中间的那幅图,将2旋上去,6旋下来,但我们发现4本来就是6的左子树,那这不是冲突了吗,不要担心。既然我们将2旋下来,就不能不要4,那就得重新给4找家了,有同学可能会想到重新遍历树给4找家,这样也没错,但是执行效率就大大降低了,那平衡二叉树的存在又有什么意义呢。我们来想一想,4比6小,现在我们将2旋下来,2的右子树就为空了,4本来就是在2的右边,是不是也就该放在2的右子树上呢。在实际代码的实现也是如此,不用在重新遍历该树给4找家直接添加就可以。在进行LL型旋转最终就平衡了.
分析了平衡二叉树的4种旋转后,接下来我们就开始写代码啦,代码中我们还会增加删除的操作-------上代码
三.代码实现
结点定义
代码如下:
/**
* AVL结点类
* @param <AnyType>
*/
public class AVLNode<AnyType> {
//数据域
AnyType element;
//指向左孩子
AVLNode<AnyType> left;
//指向右孩子
AVLNode<AnyType> right;
//当前结点的高度
int height;
AVLNode(AnyType element){
this(element,null,null);
}
AVLNode(AnyType element,AVLNode<AnyType> left,AVLNode<AnyType> right){
this.element = element;
this.left = left;
this.right = right;
height = 0;
}
}
以下该方法均包含在AVLTree类中
public class AVLTree<AnyType extends Comparable<? super AnyType>>{
/**
* 定义的高度差最大值
*/
private static final int MAX_HEIGHT_DIFFERENCE = 1;
/**
* 根结点
*/
private AVLNode<AnyType> root = null;
定义该类时使用泛型,传入的类的类型必须是实现Comparable接口,后面<? super AnyType> 是为了减少限制,传入的类型可以是AnyType也可以是AnyType的父类。
1.RR(型)
代码如下:
/**
* RR型
* @param avlNode
* @return
*/
private AVLNode<AnyType> rightRightRotation(AVLNode<AnyType> avlNode ) {
//首先获取不平衡节点的右孩子
AVLNode<AnyType> right = avlNode.right;
//将旋转中心的节点的左孩子给不平衡节点的右孩子
avlNode.right = right.left
//将旋下来的那一个节点放在旋转中心的左孩子
right.left = avlNode;
//更新两个节点的高度
avlNode.height = Math.max(height(avlNode.left), height(avlNode.right)) + 1;
right.height = Math.max(avlNode.height, height(right.right)) + 1;
//返回平衡后的根节点
return right;
}
2. LL型
代码如下:
/**
* LL型
* @param avlNode
* @return
*/
private AVLNode<AnyType> leftLeftRotation(AVLNode<AnyType> avlNode ){
//首先获取不平衡节点的左孩子
AVLNode<AnyType> left = avlNode.left;
//将旋转中心的节点的右孩子给不平衡节点的左孩子
avlNode.left = left.right;
//将旋下来的那一个节点放在旋转中心的右孩子
left.right = avlNode;
//更新两个节点的高度
avlNode.height = Math.max(height(avlNode.left),height(avlNode.right)) + 1;
left.height = Math.max(avlNode.height,height(left.left)) + 1;
//返回平衡后的根节点
return left;
}
3. LR型
代码如下:
/**
* LR型 --- 在RR在LL
* @param avlNode
* @return
*/
private AVLNode<AnyType> leftRightRotation(AVLNode<AnyType> avlNode ){
//先进行RR,更新不平衡节点的左孩子
avlNode.left = rightRightRotation(avlNode.left);
//在进行LL并且返回更新后的节点
return leftLeftRotation(avlNode);
}
4. RL型
代码如下:
/**
* RL型 --- 先LL在RR
* @param avlNode
* @return
*/
private AVLNode<AnyType> rightLeftRotation(AVLNode<AnyType> avlNode ){
//先进行LL,更新不平衡节点的右孩子
avlNode.right = leftLeftRotation(avlNode.right);
//在进行RR并且返回更新后的节点
return rightRightRotation(avlNode);
}
5. 插入
代码如下:
private void insert(AnyType key){
this.root = insertNode(this.root,key);
}
/**
* 插入结点的操作,插入一个节点就要判断
* @param avlNode
* @return
*/
private AVLNode<AnyType> insertNode(AVLNode<AnyType> avlNode,AnyType key){
//当为空时就新建一个节点,最后返回给上次一调用他的地方,即就利用链表连接上了
if (avlNode == null){
avlNode = new AVLNode<AnyType>(key,null,null);
} else{
//利用compareTo方法直接比较大小
int cmpResult = key.compareTo(avlNode.element);
//大于0,在右子树上
if (cmpResult > 0){
avlNode.right = insertNode(avlNode.right,key);
} else if(cmpResult < 0){
//小于0,在左子树上
avlNode.left = insertNode(avlNode.left,key);
} else{
//该节点已经存在不再插入
System.out.println("该结点已存在,不再添加!");
}
}
//在插入节点时直接生成当前节点的高度
avlNode.height = Math.max(height(avlNode.left),height(avlNode.right)) + 1;
//每次插入一个节点判断所有节点是否平衡
//接着没插入一个节点就判断该节点以及他的上面的节点是否平衡
return isBalanced(avlNode);
}
6. 删除
代码如下:
private void delete(AnyType key){
this.root = isFind(this.root,key);
}
/**
* 查找该结点是否存在
* @param avlNode
* @param key
* @return
*/
private AVLNode<AnyType> isFind(AVLNode<AnyType> avlNode,AnyType key){
if(avlNode == null){
System.out.println("没有找到该结点,删除失败!");
return null;
}
if(key.compareTo(avlNode.element) > 0){
isFind(avlNode.right,key);
} else if(key.compareTo(avlNode.element) < 0){
isFind(avlNode.left,key);
} else if (key == avlNode.element){
//找到要删除的节点删除它
avlNode = deleteNode(this.root,key);
}
//返回删除后的跟节点
return avlNode;
}
/**
* 删除节点
* @param avlNode
* @param key
* @return
*/
private AVLNode<AnyType> deleteNode(AVLNode<AnyType> avlNode,AnyType key){
//删除叶子时,直接返回空
if(avlNode == null){
return null;
}
if(key.compareTo(avlNode.element) > 0){
avlNode.right = deleteNode(avlNode.right,key);
} else if(key.compareTo(avlNode.element) < 0){
avlNode.left = deleteNode(avlNode.left,key);
//就是二叉排序树的删除方式,左右子树都不为空时
} else if (avlNode.left != null && avlNode.right != null){
//把右子树的最小的赋值给当前结点的数据域
avlNode.element = findMin(avlNode.right).element;
//以当前结点的右子树为根结点来删除右子树中最小的值
avlNode.right = deleteNode(avlNode.right,avlNode.element);
} else {
//为叶子或者只有一个为空的情况
avlNode = avlNode.left != null ? avlNode.left : avlNode.right;
}
//判断树上的节点是否为空
return isBalanced(avlNode);
}
/**
* 找最小结点
* @param root
* @return
*/
private AVLNode<AnyType> findMin(AVLNode<AnyType> root) {
while(root.left != null) {
root = root.left;
}
return root;
}
7. 判断平衡
代码如下:
/**
* 判断是否平衡,不平衡进行旋转,返回平衡后的结点
* @param avlNode
* @return
*/
private AVLNode<AnyType> isBalanced(AVLNode<AnyType> avlNode){
if(avlNode == null){
return null;
}
//右子树高
if (height(avlNode.right) - height(avlNode.left) > MAX_HEIGHT_DIFFERENCE ){
//结点右节点的右子树高度大于等于左子树的高度,则为RR型
//在最后讨论为什么是大于等于的情况
if (height(avlNode.right.right) >= height(avlNode.right.left)) {
avlNode = rightRightRotation(avlNode);
} else {
//反之,则为RL型
avlNode = rightLeftRotation(avlNode);
}
//左子树高
} else if(height(avlNode.left) - height(avlNode.right) > MAX_HEIGHT_DIFFERENCE ){
//结点左节点的左子树的高度大于等于右子树的高度高,则为LL情况
//同上
if (height(avlNode.left.left) >= height(avlNode.left.right)){
avlNode = leftLeftRotation(avlNode);
} else{
//在左子树的右边,LR情况
avlNode = leftRightRotation(avlNode);
}
}
//返回平衡调整后节点
return avlNode;
}
8.求高度
代码如下:
private int height(AVLNode<AnyType> avlNode){
if(avlNode != null){
return avlNode.height;
}
return -1;
}
9.验证
//中序遍历
private void Middle(AVLNode<AnyType> root){
if(root != null){
System.out.print(root.element+ " ");
Middle(root.left);
Middle(root.right);
}
}
AVLTree<Integer> integerAVLTree = new AVLTree<>();
integerAVLTree.insert(1);
integerAVLTree.insert(2);
integerAVLTree.insert(3);
integerAVLTree.insert(4);
integerAVLTree.insert(5);
integerAVLTree.insert(6);
integerAVLTree.insert(7);
integerAVLTree.insert(8);
integerAVLTree.Middle(integerAVLTree.root);//4 2 1 3 6 5 7 8
integerAVLTree.delete(4);
System.out.println();
integerAVLTree.Middle(integerAVLTree.root); //5 2 1 3 7 6 8
讨论
上面在判断为RR还是RL型(LL和LR型道理相同就不在赘述了)有一个大于等于的情况我们可以来探讨一下就是下面这两个图
第一幅是当成RR来看

第二幅是当成RL来看

我们可以看出肯定是看成RR效率更高一点,因为只需要旋转一次就可以达到平衡了,所以在判断为R~之后,再进一步判断时将相等就归为RR型了。
总结
写这个AVL树其实之前看过相关的知识,当时没有直接写下来,这一周就决定把他写出来从写出代码到写完博客大约两天的时间,删除的代码和二叉查找树的删除一样,我当时写二叉查找树时的删除代码很冗余,因为要变双亲结点的指针域,我就加了个Parent指针域,然后还判断是双亲的左孩子还是右孩子,就很复杂,但是后来发现了一种新的删除更加简洁,就是上面的代码,再接受值得时候就可以更新值了就不用判断是左子树还是右子树了。