文章目录
一. 逻辑回归算法原理及应用介绍
1.1. 逻辑回归的介绍
逻辑回归(Logistic regression,简称LR)是一个分类模型,并且广泛应用于各个领域之中。
其最为突出的两点就是其模型简单(部署快!)和模型的可解释性强(用于学术研究的因子分析 & 企业内数分的归因)。
优劣势:
优点:
1.实现简单,易于理解和实现;
2.计算代价不高,速度很快,存储资源低;
缺点:容易欠拟合,分类精度可能不高
1.2. 逻辑回归的算法原理
逻辑回归主要用于两分类问题(也可用于多分类,不过准确性会有所损失),所以利用了Logistic函数(或称为Sigmoid函数,也常见于神经网络的激活函数),函数形式为:
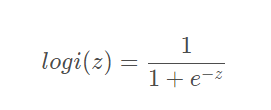
其对应的函数图像可以表示如下:
import matplotlib.pyplot as plt
x = np.arange(-5,5,0.01)
y = 1/(1+np.exp(-x))
plt.plot(x,y)
plt.xlabel('z')
plt.ylabel('y')
plt.grid()
plt.show()

通过上图我们可以发现 Logistic 函数是单调递增函数,并且在z=0的时候取值为0.5,并且logi(.)函数的取值范围是(0,1)。
而回归的基本方程为
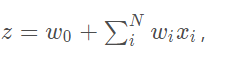
将回归方程写入其中为:
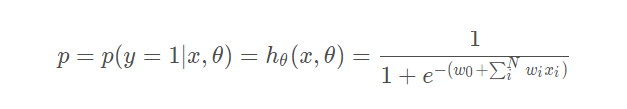
所以可以得到:
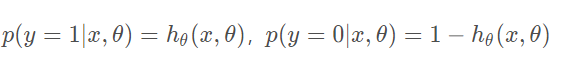
逻辑回归从其原理上来说,逻辑回归其实是实现了一个决策边界:
对于下列函数
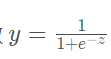
当 z = > 0时,y = > 0.5,分类为1;
当 z < 0 时,y < 0.5 ,分类为0。
其对应的y 值,我们可以视为类别1的概率预测值.
对于模型的训练而言:实质上来说就是利用数据求解出对应的模型的特定的w。从而得到一个针对于当前数据的特征逻辑回归模型。
而对于多分类而言,将多个二分类的逻辑回归组合,即可实现多分类。
1.3. 逻辑回归的应用
逻辑回归模型广泛用于各个领域,包括机器学习,大多数医学领域和社会科学。在经济学中它可以用来预测一个人选择进入劳动力市场的可能性,而商业应用则可以用来预测房主拖欠抵押贷款的可能性。自然语言处理领域也可有用于文本分类等场景(添加条件随机字段)。
逻辑回归模型现在同样是很多分类算法的基础组件,比如 分类任务中基于GBDT算法+LR逻辑回归实现的信用卡交易反欺诈,CTR(点击通过率)预估等,其好处在于输出值自然地落在0到1之间,并且有概率意义。模型清晰,有对应的概率学理论基础。它拟合出来的参数就代表了每一个特征(feature)对结果的影响。也是一个理解数据的好工具。但同时由于其本质上是一个线性的分类器,所以不能应对较为复杂的数据情况。很多时候我们也会拿逻辑回归模型去做一些任务尝试的基线(基础水平)。
二. 入门Demo
## 构造数据集
x_fearures = np.array([[-1, -2], [-2, -1], [-3, -2], [1, 3], [2, 1], [3, 2]]) # 2个特征字段(自变量)
y_label = np.array([0, 0, 0, 1, 1, 1]) # 目标字段(因变量)
## 调用逻辑回归模型(from sklearn.linear_model import LogisticRegression)
lr_clf = LogisticRegression()
## 用逻辑回归模型拟合构造的数据集
#其拟合方程为 y=w0+w1*x1+w2*x2
lr_clf = lr_clf.fit(x_fearures, y_label)
2.1. 模型参数查看
## 查看对应模型的自变量系数w(0.73,0.69)
print('the weight of Logistic Regression:',lr_clf.coef_)
## 查看其对应模型的常数项系数w0(-0.036)
print('the intercept(w0) of Logistic Regression:',lr_clf.intercept_)
2.2. 模型可视化
## 可视化构造的数据样本点
plt.figure()
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis') # 参数详解:x坐标,y坐标,颜色选择,点size大小,画布选择
plt.title('Dataset') # 画布标题
plt.show()

可以看见不同目标变量(因变量)已经用颜色加以区分,而两个特征值(自变量)已经映射到了二维坐标平面
下一步,添加逻辑回归的决策边界:
nx, ny = 200, 100
x_min, x_max = plt.xlim() # x边界
y_min, y_max = plt.ylim() # y边界
x_grid, y_grid = np.meshgrid(np.linspace(x_min, x_max, nx),np.linspace(y_min, y_max, ny))
z_proba = lr_clf.predict_proba(np.c_[x_grid.ravel(), y_grid.ravel()])
z_proba = z_proba[:, 1].reshape(x_grid.shape)
plt.contour(x_grid, y_grid, z_proba, [0.5], linewidths=2., colors='blue') # 参考线设置
plt.show()

是不是更加方便观测了呢?
那么怎么呈现新增样本点呢?
### 可视化预测新样本
plt.figure()
## new point 1 并添加指示箭头
x_fearures_new1 = np.array([[0, -1]])
plt.scatter(x_fearures_new1[:,0],x_fearures_new1[:,1], s=50, cmap='viridis')
plt.annotate(s='New point 1',xy=(0,-1),xytext=(-2,0),color='blue',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))
## new point 2 并添加指示箭头
x_fearures_new2 = np.array([[1, 2]])
plt.scatter(x_fearures_new2[:,0],x_fearures_new2[:,1], s=50, cmap='viridis')
plt.annotate(s='New point 2',xy=(1,2),xytext=(-1.5,2.5),color='red',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))
## 训练样本
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.title('Dataset')
# 可视化决策边界
plt.contour(x_grid, y_grid, z_proba, [0.5], linewidths=2., colors='blue')
plt.show()

2.3. 模型预测
## 在训练集和测试集上分布利用训练好的模型进行预测
y_label_new1_predict = lr_clf.predict(x_fearures_new1) # 对new point 1预测
y_label_new2_predict = lr_clf.predict(x_fearures_new2) # 对new point 2预测
# 预测分类结果
print('The New point 1 predict class:\n',y_label_new1_predict)
print('The New point 2 predict class:\n',y_label_new2_predict)
## 由于逻辑回归模型是概率预测模型(软分类),所以我们可以利用 predict_proba 函数预测其概率
y_label_new1_predict_proba = lr_clf.predict_proba(x_fearures_new1)
y_label_new2_predict_proba = lr_clf.predict_proba(x_fearures_new2)
# 预测概率结果
print('The New point 1 predict Probability of each class:\n',y_label_new1_predict_proba) # (0.675,0.325)
print('The New point 2 predict Probability of each class:\n',y_label_new2_predict_proba) # (0.110,0.890)
逻辑回归的分类判别是依据概率0.5的决策边界(上图蓝线)
因此可以发现训练好的回归模型将X_new1预测为了类别0(判别面左下侧),X_new2预测为了类别1(判别面右上侧)。