[IEEE754-2008] Decimal Floating-Point Number

鉴于中文互联网中关于IEEE754-2008的Decimal浮点数标准描述资料基本没有，这次先粗略的做个解读，抛转引玉

Owing to time constraints, the English version of the article is writing now.

Click here to translate the page into English version for the critical situation.

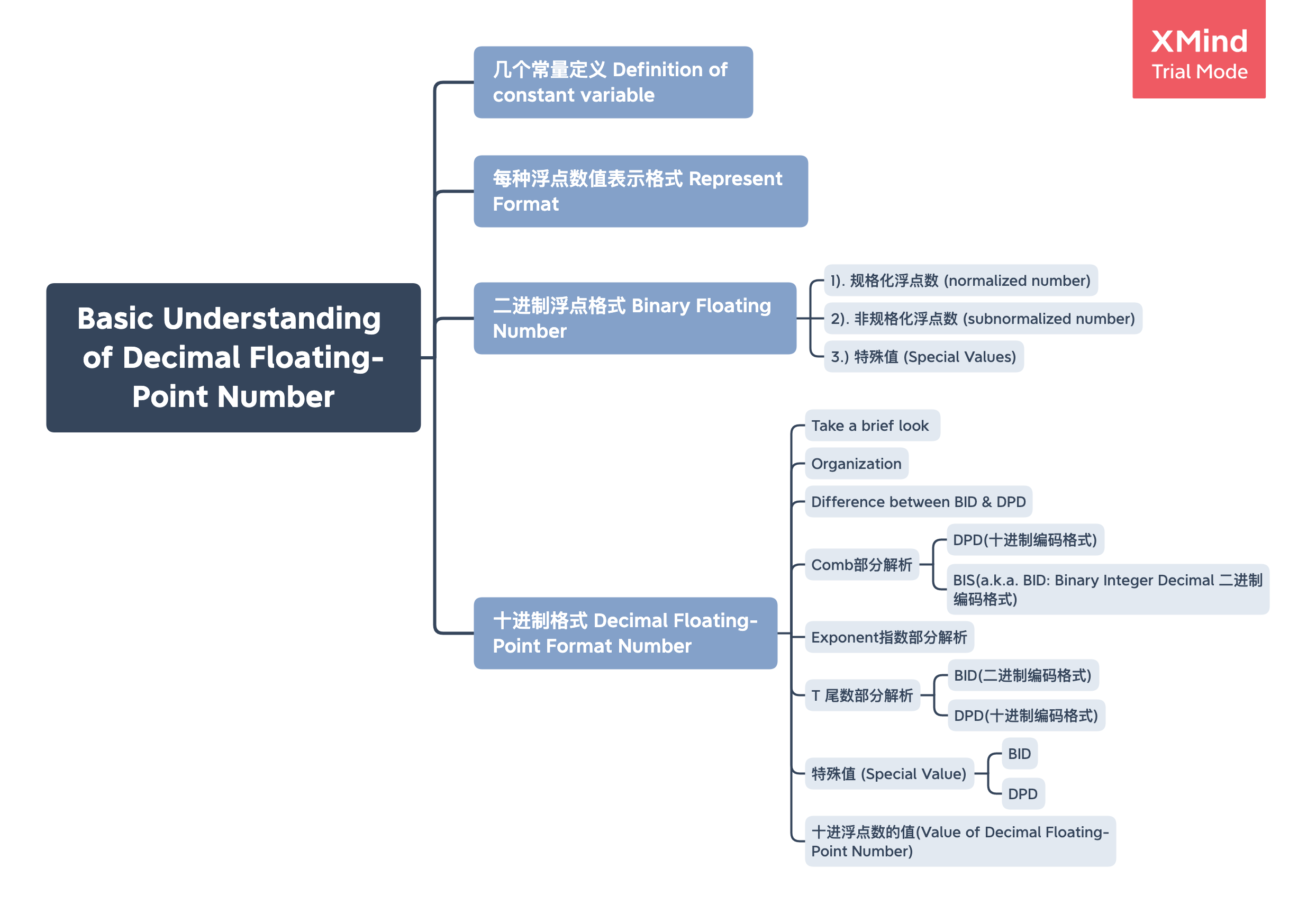
几个常量定义

1. b，基数[base]，为2或10
2. p，精度[precision]
3. emax，指数的最大可能值
4. emin，指数的最小可能值，对于所有类型，emin = 1- emax

每种浮点数值表示格式

• 每一种浮点format都由基数，编码位数(i.e binary64)

• 对于每一种浮点format，其数据域需要这样被表示

  • 带符号的0和不带符号的0的floating number的形式为

  $$(-1{)}^s\times b^e\times m$$

  1. S: is 0 or 1

2. e: emin <= e <= emax
3. m is a number represented by a digit string of the form d₀・d₁ d₂…d_p-1 where d_i is an integer digit 0<= d_i <=b(therefor 0 <= m <=b)
4. Two infinities, +∞ and −∞.
5. Two NaNs(两个非数字，Not a numbers), qNaN (quiet) and sNaN (signaling)

二进制浮点格式 Binary Floating Number

二进制浮点格式的小数是我们熟知的小数表示方式，也是IEEE754-1985中小数表示的标准。

一个二进制浮点数将会被表示成这种形式：

1. S: 符号位 1-bit
2. E: 指数位 w-bit E = e + bias
3. T: 尾数 t-bit t = p - 1, T = d1d2⋯dp−1 [di: s2进制]

参数	binary16	binary32	binary64	binary128	binary{k}
k	16	32	64	128	k, 32|k
p	11	24	53	113	k-round(4log2 k)+13
emax	15	127	1023	16383	2^{k-p-1}-1
bias(辅助偏移值/置偏值)	15	127	1023	16383	emax
sign bit	1	1	1	1	1
w	5	8	11	15	round(4log2 k)−13
t	10	23	52	112	k-w-1

1). 规格化浮点数 (normalized number)

E为8位的无符号整数，表示范围为0～255，E-bias表示范围为-127 ～ 128

但格式化浮点数要求 E₀ ~ E_w-1 不全为0(E为0, E-bias为-127)或不全为1(E为255, E-bias为128)的情况，此时浮点数公式为：(-1)^S × 2^E-bias × m。

E-bias: (-127, 128)

T要求表示为大于等于1小于等于2的科学计数法表示的小数

S, E, T在相应块表示成二进制数

m = 1 + 2^-t T = 1 + ∑(i: 1 ~ t) 2^-id_i

Example:

float(binary32): 9.0

-> 转成二进制：1001.0

-> 使用上述公式表示：-1⁰ * 2^(3+127) * 1.001 -> -1⁰ * 2⁽¹³⁰⁾ * 1.001 (bias: 127)

-> 分区模型：

S(+) E(130) T(1)

0 10000010 00000000000000000000001

Tip.

为什么会有bias(kind of offset)存在？(Why does bisa exist?)

对于E（指数）E是一个无符号整数所以E的取值范围为（0~ 255），但是在计数中指数是可以为负的，且出于范围对称考量，所以规定在存入E时，在它原本的值上加上中间数（127），在使用时减去中间数（127），这样E的真正取值范围就成了（-127~128）。

2). 非规格化浮点数 (subnormalized number)

E₀ ~ E_w-1为0(E为0, E-bias的exponent规定为-126[不是-127，出于无法表示的异常])的情况，此时leading bit从1变为0。

因为 0<= T< 2^t, 1<= m < 2，规格化浮点数无法表示 0 ，因此规定：当一个数字的绝对值小于 b^emin时转为非规格化表示，浮点数的值由公式：(−1)^S×2^emin−tT = (-1)^S2^emin∑(i=1 ~ t) 2^-id_i

得到，此时0的表示是除了符号位之外的其他位全为0.

3.） 特殊值 (Special Values)

+∞：S – 0 E – E_i = 1 T = 0

-∞: S – 1 E – E_i = 1 T = 0

NaN：E上每一位都为1，除去上面两个特殊值，都是NaN

quiet NaN 和 signaling NaN区别在于significand段的标记(flag)位

quiet NaN不会引发任何额外的异常（ FPU 不会产生硬件异常），它们会在大多数操作中被使用。例外情况是，不能简单地将NaN原封不动地传递给输出，例如在格式转换或某些比较操作中。

与此相反的则是signaling NaN

十进制格式 Decimal Floating-Point Format Number

Take a brief look

Decimal Floating-Point format number has two encoding method, one called DPD(Densely Packed Decimal), and the other called BIS(a.k.a BID Binary Integer Decimal).

十进制浮点格式数有两种编码方法，一种称为DPD(密集打包十进制为基数的小数)，另一种称为BIS(又名 BID 二进制整数表示的十进制为基数的小数)。

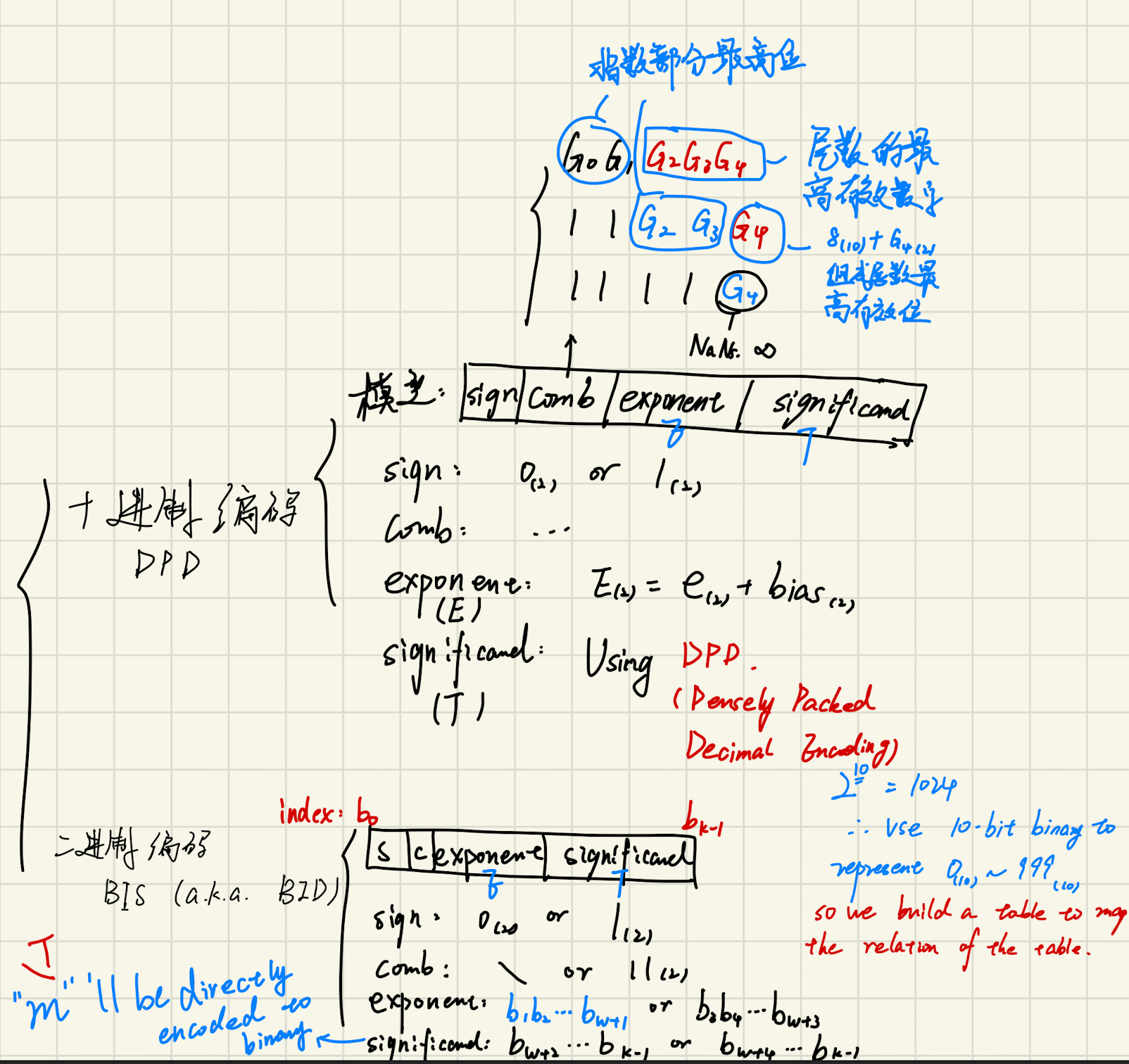
Organization

1. S: 符号位 1-bit
2. Comb: 组合部分
3. E: 指数位 w-bit E = e + bias
4. T: 尾数 t-bit t = p - 1, T = d1d2⋯dp−1 [d_i: 2进制]

参数	decimal32	decimal64	decimal128	decimal{k}
k	32	64	128	k, 32|k
p	7	16	34	9k/32-2
emax	96	384	6144	3*2^(k/16+3)
bias	101	398	6167	emax+p-2
sign bit	1	1	1	1
w	6	8	12	k/16+4
t	20	50	110	15*k/16-10

Difference between BID & DPD

BID编码与另一种DPD编码每一个部分都是最终编码成二进制进行存储，区别是在significand这段，BID编码是直接取科学计数法的有效数字部分将其转化二进制进行存储，DPD编码使用一个映射表，每3位10进制数字对应10位2进制数字，进行存储。

对于十进制编码的方式，某些硬件上直接支持十进制处理，例如IBM的POWER系列，这时直接使用该标准对数字进行存储计算等处理，否则需要使用DPD编码转化二进制进行存储。

Comb部分解析

针对两种情况：In both cases, the most significant 4 bits of the significand (which actually only have 10 possible values[0~9十个数字]) are combined with the most significant 2 bits of the exponent (3 possible values) to use 30 of the 32 possible values of a 5-bit field. The remaining combinations encode infinities and NaNs.

Combination field	Exponent Msbits	Significand Msbits	Other
00mmm	00	0mmm	—
01mmm	01	0mmm	—
10mmm	10	0mmm	—
1100m	00	100m	—
1101m	01	100m	—
1110m	10	100m	—
11110	—	—	±Infinity
11111	—	—	NaN. Sign bit ignored. First bit of exponent continuation field determines if NaN is signaling.

• 对于Significand Msbits 的 0 100在实际的significand表示中是不被表示的，这部分在结合部分(Comb)可以得出

DPD(十进制编码格式)

对于Decimal64，Comb部分由5位构成，这五位分别来自于指数(E)和尾数(T)部分

• G₀G₁ G₂G₃G₄

  G₀G₁是指数部分的最高两位

  G₂G₃G₄是尾数的最高有效位

• 11 G₂G₃ G₄

  G₂G₃ : 指数部分最高两位

  G₄: 8₍₁₀₎ + G_{4 (2)}组成位数的最高有效数字

• 1111 G₄

  表示特殊值，无穷大或NaN

BIS(a.k.a. BID: Binary Integer Decimal 二进制编码格式)

在二进制编码方案中，上图的comb和exponent部分才是真正的组合部分(RComb)，exponent 的具体位置由组合部分的前两个字节决定。

对这种数字内存模型每个位编号，b₀ b₁…b_k-1

• 当b₁b_{2 (2)} != 11₍₂₎，b₁b₂和其后的 w 位组成指数部分，剩下为尾数部分。
• 当b₁b_{2 (2)} == 11₍₂₎，b₃b_{4 (2)} != 11₍₂₎，b₃b₄ 和其后的 w 位组成指数部分，剩下为尾数部分。
• ∞，NaN与十进制编码一致

指数部分解析

指数部分由组合部分的两个比特和剩余的 w 个比特组成，由于组合部分的两个比特不可能为 11 ，组合部分中的指数部分共 3 种取值(00, 01, 10)。因此指数的所有可能取值总计有 3 * 2^w 种。

十进浮点数的指数部分也和二进浮点数的指数部分一样，是由二进制表示的 E 减去一个置偏值 bias 。为什么置偏值不是恰好是 3 * 2^w-1 ，这是因为此处的指数直接和 T 相乘，和二进浮点数乘以规格化(Normalizated)的 T 不同，这里没有规格化浮点数，因此置偏值比 3 * 2^w-1 多出来的部分就相当于规格化后多乘的值，这也是那个 bias = emax+p-2 中 p-2 的由来。

尾数部分解析

尾数部分的最高位在组合部分中，剩余部分在最后的 t (Decimal64就是50) 个比特中。

BID(二进制编码格式)

如果采用二进制编码方式， t直接按照二进制解析存入。

拿Decimal64举例子，significand区域有50二进制位的存储空间，数字有10(significand中最高位0～9) * 2⁵⁰ - 1种可能，但是数据大于10¹⁶-1是非法的，标准将其当作是0

DPD

使用此表表示数更能节省存储空间

如果采用十进制编码方式，将 t 拆成十个十个一组，每组解码出 3 个十进制整数，和组合部分的一个数字拼接成一个十进制的数字，因此十进制编码方式的最大值为 (10^3t/10+1-1) * 10^emax-p+1 。

具体如何将一组三个十进制数字(0~999)对应成一组10个二进制数字需要通过查询下表得知。

CHART FROM WIKIPEDIA

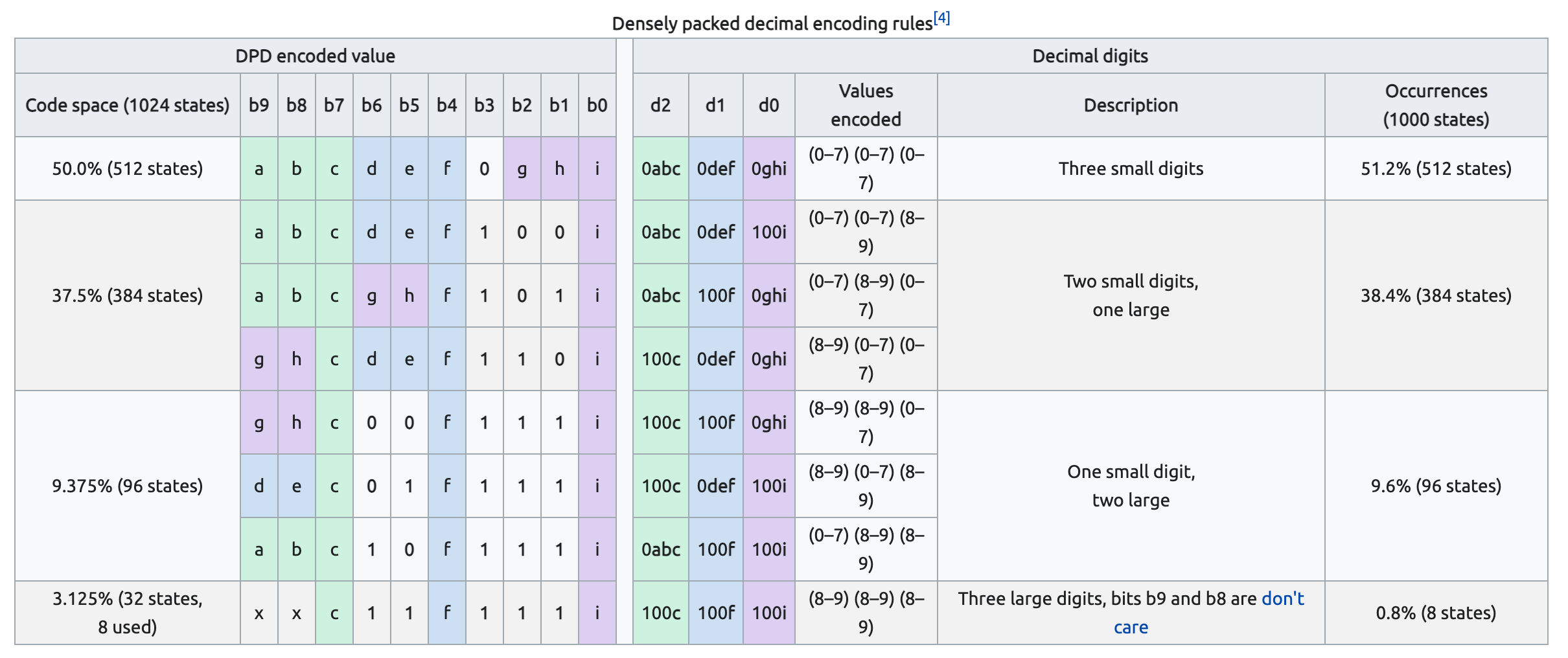
左侧是经过DPD编码过的值，右侧是初始的三位十进制数字

I.E. 我们来解释一下第三行

两侧绿色的abc，紫色的ghi，蓝色的f是同样的二进制数字，不过相对位置可能不同而已。

左侧的DPD编码后的二进制数字序列abcghf 1 0 1 i对应编码三位前十进制数，这三位十进制数表示成二进制分别为0abc 100f 0ghi

如何使用公式来表达？

0abc₍₂₎ * 100₍₁₀₎ + 100f₍₂₎ * 10₍₁₀₎ + 0ghi₍₂₎ * 1₍₁₀₎

即

[0b₉b₈b₇]₍₂₎ * 100₍₁₀₎ + [100b₄]₍₂₎ * 10₍₁₀₎ + [0b₆b₅b₀]₍₂₎ * 1₍₁₀₎

特殊值 (Special Value)

和二进浮点数类似，当组合部分前 4 个比特均为 1 的时候该浮点数表示一个特殊值。其中，第 5 个比特为 0 则表示为无穷大，第 5 个比特为 1 则表示 NaN 。和二进浮点数类似的，第 5 个比特之后的一个比特如果为 0 则为 quiet NaN ，否则为 signaling NaN 。

十进浮点数的值(Value of Decimal Floating-Point Number)

(-1)^S * T * 10^{E - bias}

其中的T和E的值都是由组合部分和各自延续部分(尾数)共同计算得出来的。

Reference

decimal64 floating-point format - Wikipedia

Decimal floating point - Wikipedia