引言
小组2020年的免试题的四位出题人是:小组18级成员李兆龙,20级成员赵子玮,刘树杭,任子涧。
同时19级成员周阔,戚凯萌,胡哲宁,李毅恒参与题目审查与展示工作。
目前题目链接还没有下线,想要挑战的同学可以继续尝试挑战。
好了,现在让我们来开启一场头脑风暴吧!
题解并不是我一个完成的,而是把几份题解拼在一起。
第一关
题目地址:q.xiyoulinux.org

首先,首页没有任何可以点击的触发事件,直接看网页源码,
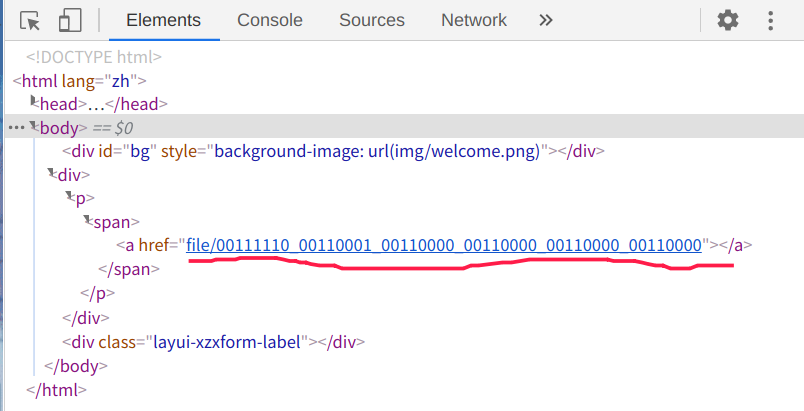
可以看到这里有一个奇怪的文件,文件名00111110_00110001_00110000_00110000_00110000_00110000
一共 8 组数字,每组 8 位数 用下划线隔开,每组数字
分别转换成 ASCII 字符得到>10000的结果
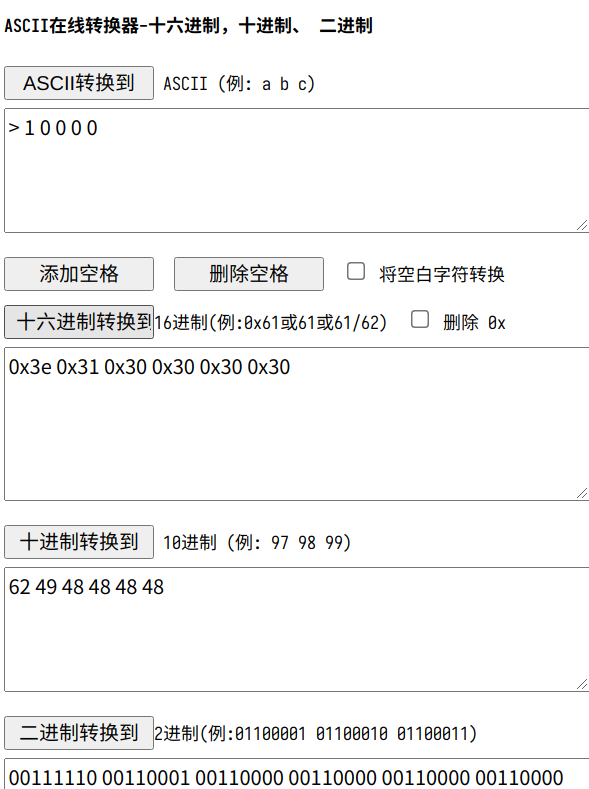
打开文件,好家伙全是 01 串,文件下载下来编辑器打开,找到第10001行,我们注意到一个奇怪的现象,
之前所有行都是80列,从10001行开始出现了81列,10009行又出现了80列,10010行
是81列,直到10710行以后又恢复成整齐的80列
竖着来看,突出的第81列每 8 行空一行,一共出现 79 组,根据先前的经验,我们将突出的这 81 列提取出来,得到一个 01 串
01101100 01100101 01110011 01110011 00100000 00110000 00110000 00110001 00110001 00110001 00110001 00110001 00110000 01011111 00110000 00110000 00110001 00110001 00110000 00110000 00110000 00110001 01011111 00110000 00110000 00110001 00110001 00110000 00110000 00110000 00110000 01011111 00110000 00110000 00110001 00110001 00110000 00110000 00110000 00110000 01011111 00110000 00110000 00110001 00110001 00110000 00110000 00110000 00110000 01011111 00110000 00110000 00110001 00110001 00110000 00110000 00110000 00110000 01111100 01100111 01110010 01100101 01110000 00100000 00100010 00110000 00110001 00110000 00110001 00110000 00110001 00110000 00100010 01111100 01110111 01100011 00100000 00101101 01101100
翻译过来就是
less 00111110_00110001_00110000_00110000_00110000_00110000|grep "0101010"|wc -l

熟悉 linux 的同学这下就看懂了,则是一条命令,我们打开终端在这个二进制文件的所在目录执行,得到了
18451这个结果。
我们翻到 18451 行,观察后发现 18454 行与 18451 行完全相同,
尝试解析中间的 18451 行到 18454 行的内容,得到了出乎意料的答案
00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000
01101000 01110100 01110100 01110000 00111010 00101111 00101111 01100100 01110111 01111010
00101110 01101101 01101011 00101111 01011010 00110111 01101110 01000101 01010010 01110110
00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000 00100000
http://dwz.mk/Z7nERv
Awesome!
第一关通关
第二关
题目地址:http://q.xiyoulinux.org/a4wpAj

网页上只有三个东西:一首诗、一张奇奇怪怪的图片以及一段音乐。无视那个版权声明
这段音乐貌似没有什么特别之处,只是一首优美的纯音乐…我们先从图片入手。
这首李白的诗提到了彩虹,彩虹的成因大家都知道:阳光因为折射发生色散。而计算机中表示颜色的方法是什么呢?这个相信读者也知道:将每种颜色“拆分”成红绿蓝三种颜色,用三个 0-255 的整数分别表示三种颜色的“量”。这就是众所周知的rgb颜色表示法。如果再仔细观察这张图片,会发现这张图片是半透明的。如果读者把这张图片下载下来,会发现这张图片是png格式的。png格式的图片是支持透明度的,除了用3个 0-255 的整数来表示红绿蓝的“量”之外,还有一个 0-255 的值alpha表示透明度。这就是rgba颜色表示法。
在这张图片中,每一个小方格对应一种颜色,每种颜色
对应了4个 0-255 的值,也就是4个字节。所以这张图片中是存储着某些数据的。我们可以用Python中的图片处理库Pillow来解码。
from PIL import Image
from typing import List
from typing import Tuple
# 图片的路径
photo_path = "photopath"
# 方块的大小,可以通过图片的尺寸和一行(列)的方块的数量算出。单位是像素。
block_size: int = 30
def get_block_count(image: Image) -> int:
return int(image.width / block_size)
def decode(photo_path: str) -> List[List[int]]:
image: Image = Image.open(photo_path)
block_count: int = get_block_count(image)
groups: List[List[int]] = []
for i in range(block_count):
for j in range(block_count):
color: Tuple[int] = image.getpixel(
(j * block_size + 5, i * block_size + 5))
groups.append(list(color))
return groups
def to_bytes(groups: list[List[int]]) -> bytes:
file_bytes: bytes = b""
for i in groups:
for j in i:
file_bytes += chr(j).encode("utf-8")
return file_bytes
if __name__ == "__main__":
with open("src.txt", "wb") as src_file:
src_file.write(to_bytes(decode(photo_path)))
src_file.close()
解码结果如下:
.file "showoffsets.c"
.text
.section .rodata.str1.1,"aMS",@progbits,1
.LC0:
.string "%zu\n"
.section .text.startup,"ax",@progbits
.p2align 4
.globl main
.type main, @function
main:
.LFB11:
.cfi_startproc
pushq %r12
.cfi_def_cfa_offset 16
.cfi_offset 12, -16
pushq %rbp
.cfi_def_cfa_offset 24
.cfi_offset 6, -24
leaq .LC0(%rip), %rbp
pushq %rbx
.cfi_def_cfa_offset 32
.cfi_offset 3, -32
leaq array(%rip), %rbx
leaq 168(%rbx), %r12
.p2align 4,,10
.p2align 3
.L2:
movq (%rbx), %rsi
movq %rbp, %rdi
xorl %eax, %eax
addq $8, %rbx
call printf@PLT
cmpq %r12, %rbx
jne .L2
popq %rbx
.cfi_def_cfa_offset 24
xorl %eax, %eax
popq %rbp
.cfi_def_cfa_offset 16
popq %r12
.cfi_def_cfa_offset 8
ret
.cfi_endproc
.LFE11:
.size main, .-main
.globl arraySize
.section .rodata
.align 8
.type arraySize, @object
.size arraySize, 8
arraySize:
.quad 21
.globl array
.data
.align 32
.type array, @object
.size array, 168
array:
.quad 1555019
.quad 1561326
.quad 1561326
.quad 1561291
.quad 1556547
.quad 1561304
.quad 1560062
.quad 1560062
.quad 1561320
.quad 1557817
.quad 1560302
.quad 1561329
.quad 1561332
.quad 1561295
.quad 1560062
.quad 1559069
.quad 1560300
.quad 1561390
.quad 1560305
.quad 1561349
.quad 1560317
.ident "GCC: (GNU) 10.2.0"
.section .note.GNU-stack,"",@progbits
嗯?这是个啥?如果读者熟悉gcc编译器,会发现这是一段由gcc编译出的汇编语言程序。
我们用gcc汇编并链接成可执行文件,然后执行:
gcc showoffsets.s
然后执行这个可执行程序:会输出以下文本:
1555019
1561326
1561326
1561291
1556547
1561304
1560062
1560062
1561320
1557817
1560302
1561329
1561332
1561295
1560062
1559069
1560300
1561390
1560305
1561349
1560317
嗯?这又是个啥???
我们仔细观察这个汇编文件,发现汇编文件是由一个叫showoffsets.c的文件编译出来的,所以这些数字可能是某个文件的偏移量。在这个网页上,还有一段音乐没有用到,那这些偏移量极有可能就是这个音乐文件的偏移量了。我们在用万能的Python将这些偏移量对应的字节连接起来。
from typing import List
offsets: List[int] = [0x17ba4b,
0x17d2ee,
0x17d2ee,
0x17d2cb,
0x17c043,
0x17d2d8,
0x17cdfe,
0x17cdfe,
0x17d2e8,
0x17c539,
0x17ceee,
0x17d2f1,
0x17d2f4,
0x17d2cf,
0x17cdfe,
0x17ca1d,
0x17ceec,
0x17d32e,
0x17cef1,
0x17d305,
0x17cefd]
# 音乐文件的路径
music_path: str = "music_path"
def decode(music_path: str) -> str:
str_bytes: bytes = b""
with open(music_path, "rb") as music_file:
music_bytes: bytes = music_file.read()
music_file.close()
for i in offsets:
str_bytes += chr(music_bytes[i]).encode("utf-8")
return str_bytes.decode("utf-8")
if __name__ == "__main__":
print(decode(music_path))
Python输出结果是:https://dwz.mk/7fAjEr
哈?这不就是第3题的url吗?
第三关
题目地址:https://dwz.mk/7fAjEr

这道题目的提示其实已经非常明确了,重要的点有两个,一点是树,一点是颜色。
所以答案已经呼之欲出了,那就是红黑树!奇了怪了,为什么这里会出现四种颜色呢,如果对红黑树的旋转操作了解的话就会清楚其实在红黑树的删除操作中有一种很特殊的旋转方式。首先我们来看看删除操作的一般过程。
删除操作首先要确定待删除节点有几个孩子,如果有两个孩子,不能直接删除该节点。而是要先找到该节点的前驱(该节点左子树中最大的节点)或者后继(该节点右子树中最小的节点),然后将前驱或者后继的值复制到要删除的节点中,最后再将前驱或后继删除。由于前驱和后继至多只有一个孩子节点,这样我们就把原来要删除的节点有两个孩子的问题转化为只有一个孩子节点的问题。
此时如果要删除的节点为红色不违背红黑树约束,但是如果是黑色节点则违背约束,此时需要进行旋转操作,大多数的删除操作对子树节点颜色有明确定义,但是其中有一种旋转操作不需要,即如下这种情况:

所以这里把题目中的图案映射到图中左边的树,进行一个旋转操作就可以得到另外一颗树,把它按题目规则序列化则可得到正确答案。
即:122332312
第四关
题目地址:http://q.xiyoulinux.org/e9ON0C
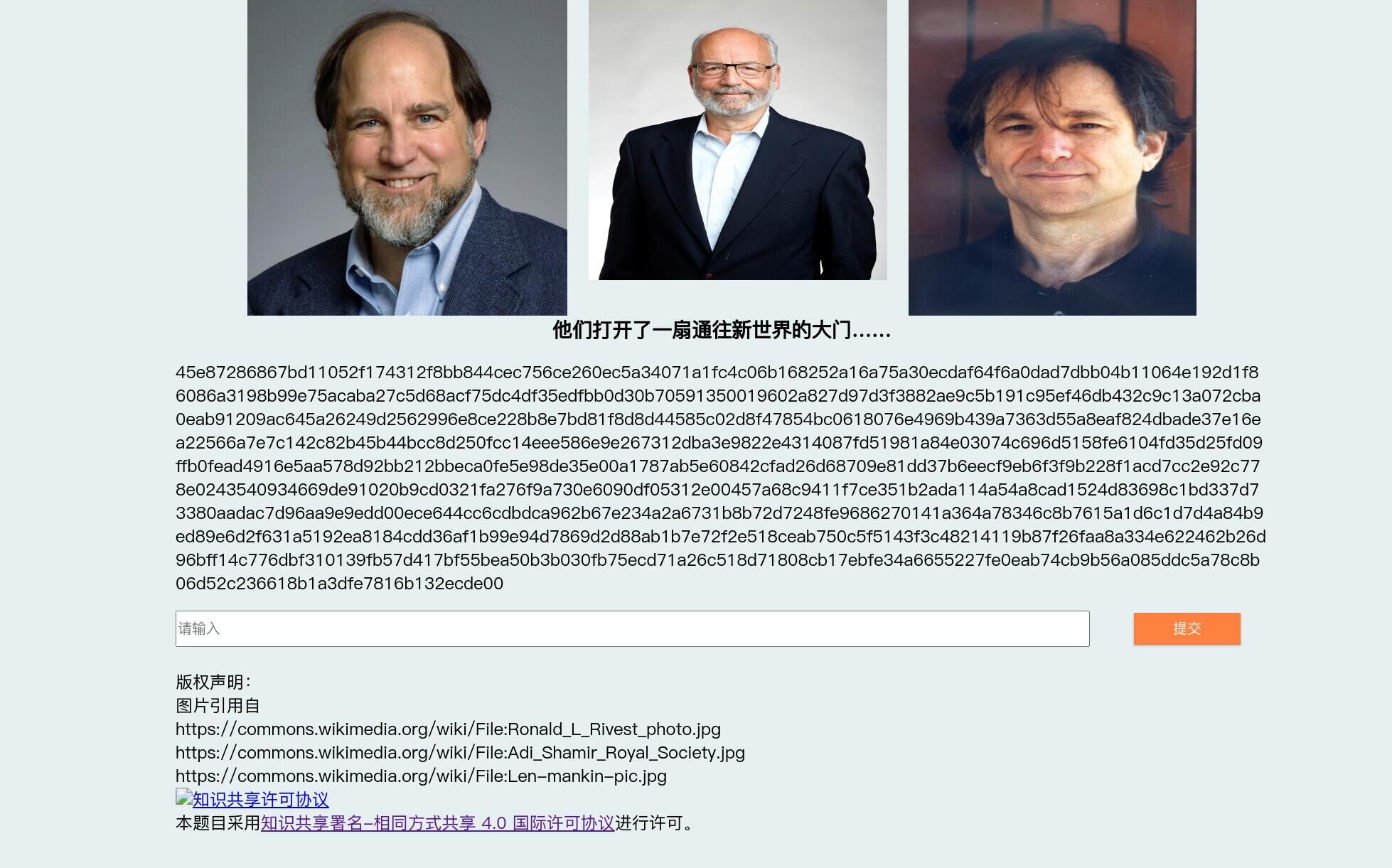
本题目的考察点在于 RSA 算法。
打开网页就能清晰的看到网页上有一串莫名其妙的字符串,仔细观察后会发现他们只含有 0-9 和 a-f,相信所有的人都能想到这就是一个 16 进制数。
45e87286867bd11052f174312f8bb844cec756ce260ec5a34071a1fc4c06b168252a16a75a30ecdaf64f6a0dad7dbb04b11064e192d1f86086a3198b99e75acaba27c5d68acf75dc4df35edfbb0d30b70591350019602a827d97d3f3882ae9c5b191c95ef46db432c9c13a072cba0eab91209ac645a26249d2562996e8ce228b8e7bd81f8d8d44585c02d8f47854bc0618076e4969b439a7363d55a8eaf824dbade37e16ea22566a7e7c142c82b45b44bcc8d250fcc14eee586e9e267312dba3e9822e4314087fd51981a84e03074c696d5158fe6104fd35d25fd09ffb0fead4916e5aa578d92bb212bbeca0fe5e98de35e00a1787ab5e60842cfad26d68709e81dd37b6eecf9eb6f3f9b228f1acd7cc2e92c778e0243540934669de91020b9cd0321fa276f9a730e6090df05312e00457a68c9411f7ce351b2ada114a54a8cad1524d83698c1bd337d73380aadac7d96aa9e9edd00ece644cc6cdbdca962b67e234a2a6731b8b72d7248fe9686270141a364a78346c8b7615a1d6c1d7d4a84b9ed89e6d2f631a5192ea8184cdd36af1b99e94d7869d2d88ab1b7e72f2e518ceab750c5f5143f3c48214119b87f26faa8a334e622462b26d96bff14c776dbf310139fb57d417bf55bea50b3b030fb75ecd71a26c518d71808cb17ebfe34a6655227fe0eab74cb9b56a085ddc5a78c8b06d52c236618b1a3dfe7816b132ecde00
除此之外,网页最上部的三张照片也指引了另一个线索。通过图片搜索或者直接查看网页下方的版权声明就可十分容易得知这三张照片对应的人物分别是: Ronald Linn Rivest、Adi Shamir、Leonard Adleman。发现了三个人的名字后,查查他们是谁,从他们三人的简介中不难发现他们 3 人是 RSA 算法的发明者。
在此,感谢 Ronald Linn Rivest、Adi Shamir、Leonard Adleman 发明 RSA 算法一事为计算机科学作出的杰出贡献,他们打开了通往非对称加密算法的大门。
结合上面的十六进制数与 RSA 算法这个线索,我想不难猜到那串 16 进制数便是使用 RSA 算法加密后得到的密文了。
通过查找相关资料,就会发现 RSA 算法的解密是十分困难的,RSA 算法的可靠性来源于对大数进行因数分解的数学问题。
无论如何,不可能在只有密文的情况下完成解密。
回想图片下方的那句话「他们打开了一扇通往新世界的大门……」,这句话自然不仅仅是对他们三人的功绩的赞叹,更是暗含了本题的提示:「这三张图片是通往下一关的大门的钥匙」。我相信结合整个题目的语境,不难理出这层含义。
下载这三张图片,用 16 进制编辑工具打开,在图片的最后面便可发现出题人给出的信息
e=65537
p=25862393087395144904578136066432622071613031108961508523776645974920112279571321274880403508998728336416174207954650261632773395336341858263117921946924709870308337780316993582832462776992833790440844633839729622746959330775633201140396009253194156382940738022047306941239966667693815888617107292778086039906056984287341581589863951680315082177719811893617114865593727125600782409006574479692430841244064660640437304837974726422158658744419697666717354373939752082268152242347379175058796398284230036914365748933140856442051681786956193712489422851825444698625063619154124978192545710964521177077153134997996710676819
q=29404999009444129808207101477302908884432848806969786898545939981324275388514204221673553167648241936370278958848658876075010146581347728219935243641031572735178324398168430951159612634336354969866091993303600114502652385983156726049132047290354556664894573942338038767376264479356691953013331654008659792346607521273164498138004555036020341291404697545594383622685494235403111339833079531850829660280651225344340068461823095092950097635435100884314446767160779554365653863499309534183976510778377077896265226321210788500229578828827219348128512401723649114755662577546818759852162552127571807817650455670247102677521
好了,现在获得了 e、p、q 就可以开始解密了。
下面将讲述如何手动对 RSA 算法进行解密。当然互联网上有大量的 RSA 算法的解密工具,通过工具完成解密也是完全没问题的。
解密密文需计算出 d。根据 RSA 算法有:
e d ≡ 1 ( m o d φ ( n ) ) ed\equiv1 \pmod{\varphi(n)} ed≡1(modφ(n))
n = p q n=pq n=pq
并且
gcd ( p , q ) = 1 \gcd(p,q)=1 gcd(p,q)=1
又根据欧拉定理得到
φ ( n ) = ( p − 1 ) ( q − 1 ) \varphi(n)=(p-1)(q-1) φ(n)=(p−1)(q−1)
若用 C C C 表示消息的密文,用 M M M 表示消息的明文,求得 d d d 之后,通过
M ≡ C d ( m o d n ) M\equiv C^d\pmod{n} M≡Cd(modn) 就能得到明文了。
好了,思路通顺了。现在求解 d d d。
有人可能要疑惑,为什么要出这样的一道题。这道题的选择事实上也经过了一些深思,我希望免试题不只是「脑筋急转弯式」的游戏,更能从中看出作答者的部分能力。这也是我作为出题人对答题者的尊重。
答题者若使用工具完成本题,那说明答题者具有良好的信息收集能力、有细心观察的能力、有用简单的方式解决问题的能力。
答题者若是通过编程的方式运用一定的算法思想解决本题,那答题者或许会用到同余的性质、模意义下的乘法逆元等数论知识,也需要掌握扩展欧几里德、快速幂等算法知识。还可能需要手动处理大数运算的问题。
为了便于计算,题解中使用 Python 进行演示。
def exgcd(a, b, arr):
if b == 0:
arr[0] = 1
arr[1] = 0
return a
gcd = exgcd(b, a % b, arr)
arr[0], arr[1] = arr[1], arr[0]-(a//b)*arr[1]
return gcd
def modularMultiplicativeInverse(a, n):
tmp = [0, 0]
exgcd(a, n, tmp)
return (tmp[0] % n+n) % n
def quickPower(a, b, n):
result = 1
while b > 0:
if b & 1:
result *= a
result %= n
a *= a
a %= n
b >>= 1
return result % n
p = 25862393087395144904578136066432622071613031108961508523776645974920112279571321274880403508998728336416174207954650261632773395336341858263117921946924709870308337780316993582832462776992833790440844633839729622746959330775633201140396009253194156382940738022047306941239966667693815888617107292778086039906056984287341581589863951680315082177719811893617114865593727125600782409006574479692430841244064660640437304837974726422158658744419697666717354373939752082268152242347379175058796398284230036914365748933140856442051681786956193712489422851825444698625063619154124978192545710964521177077153134997996710676819
q = 29404999009444129808207101477302908884432848806969786898545939981324275388514204221673553167648241936370278958848658876075010146581347728219935243641031572735178324398168430951159612634336354969866091993303600114502652385983156726049132047290354556664894573942338038767376264479356691953013331654008659792346607521273164498138004555036020341291404697545594383622685494235403111339833079531850829660280651225344340068461823095092950097635435100884314446767160779554365653863499309534183976510778377077896265226321210788500229578828827219348128512401723649114755662577546818759852162552127571807817650455670247102677521
e = 65537
d = modularMultiplicativeInverse(e, (p-1)*(q-1))
ciphertext = 0x45e87286867bd11052f174312f8bb844cec756ce260ec5a34071a1fc4c06b168252a16a75a30ecdaf64f6a0dad7dbb04b11064e192d1f86086a3198b99e75acaba27c5d68acf75dc4df35edfbb0d30b70591350019602a827d97d3f3882ae9c5b191c95ef46db432c9c13a072cba0eab91209ac645a26249d2562996e8ce228b8e7bd81f8d8d44585c02d8f47854bc0618076e4969b439a7363d55a8eaf824dbade37e16ea22566a7e7c142c82b45b44bcc8d250fcc14eee586e9e267312dba3e9822e4314087fd51981a84e03074c696d5158fe6104fd35d25fd09ffb0fead4916e5aa578d92bb212bbeca0fe5e98de35e00a1787ab5e60842cfad26d68709e81dd37b6eecf9eb6f3f9b228f1acd7cc2e92c778e0243540934669de91020b9cd0321fa276f9a730e6090df05312e00457a68c9411f7ce351b2ada114a54a8cad1524d83698c1bd337d73380aadac7d96aa9e9edd00ece644cc6cdbdca962b67e234a2a6731b8b72d7248fe9686270141a364a78346c8b7615a1d6c1d7d4a84b9ed89e6d2f631a5192ea8184cdd36af1b99e94d7869d2d88ab1b7e72f2e518ceab750c5f5143f3c48214119b87f26faa8a334e622462b26d96bff14c776dbf310139fb57d417bf55bea50b3b030fb75ecd71a26c518d71808cb17ebfe34a6655227fe0eab74cb9b56a085ddc5a78c8b06d52c236618b1a3dfe7816b132ecde00
message = quickPower(ciphertext, d, p*q)
buf = []
while message > 0:
buf.append(message & 0xFF)
message >>= 8
buf.reverse()
for i in buf:
print(chr(i), end="")
print()
可以看到输出的结果为
RSAis1Public-KeyCrypt0systemThat1sWidelyusedForSecureDa7aTransmission.
在网页中唯一的输入框提交即可进入第 5 题。
细心的话,不难发现是最终结果为这句话的变式:
RSA is a public-key cryptosystem that is widely used for secure data transmission.[1]
在此,请允许我以及XiyouLinuxGroup全体成员再次表达对「在计算机科学领域作出杰出贡献的科学家」的敬意。
第五关
题目地址:http://q.xiyoulinux.org/ieskd
第 5 题原计划为对并查集的考察,但由于一些原因最终替换为了本题。
本题并没有考察什么算法的思想。打开本题网站,最先看到的就是一个 XiYou Linux Group 小组成立 15 周年的纪念图。
当然,纪念图不可能毫无缘由的出现在题目中,正如你所猜测的那样:纪念图实际上是本题目的提示。
可以看到,图片下方有一句「请扫码:」,里面还含有一个「冒号」!!!如果能联想到后文的字符串大概是一个二维码就解决了本题的一大半。
实际上,只要使用图片中出现的 15 也就是 0xF 与每个字符进行 XOR 操作并将其输出,就能得到本题的答案,也就是本题需要去扫描的二维码了。
#include <stdio.h>
#include <stdlib.h>
unsigned char buf[50000];
int main() {
FILE *input = fopen("/home/xiyoulinux/5.txt", "r");
if (!input) {
perror("找不到源文件");
exit(EXIT_FAILURE);
}
ssize_t size = fread(buf, sizeof(buf[0]), sizeof(buf), input);
if (size <= 0) {
perror("读取失败");
exit(EXIT_FAILURE);
}
ssize_t i;
for (i = 0; i < size; i++)
buf[i] ^= 0x0F;
buf[i] = '\n';
if (fclose(input)) exit(EXIT_FAILURE);
FILE *output = fopen("displayQRcode.txt", "w");
if (!output) {
perror("创建 displayQRcode.txt 失败");
exit(EXIT_FAILURE);
}
if (fwrite(buf, sizeof(char), i, output) != i) {
perror("写入 displayQRcode.txt 失败");
exit(EXIT_FAILURE);
}
if (fclose(output))
perror("关闭文件失败");
}
作为结果的二维码非常的大,答题者可能需要经过一定的缩放才能正常的扫描。
扫描二维码后得到一个字符串:
`c)Ic#/lFKyk?#R5
这个字符串由什么用?看看网站中宣传图中的微信公众号二维码,可以想到去将字符串发送给微信公众号。
发送后将收到公众号的宣布你通关的消息。
第 4 题、第 5 题 题解采用 知识共享署名-相同方式共享 4.0 国际许可协议进行许可。

总结
免试题的目的不在于为了刁难参与者而设立,而是在于为了激发每一个对技术有不懈追求的极客!
时代的变迁飞速,今时也早已不同于往日,数据库,操作系统内核,分布式,Web应用,服务端编程等等简单的名词背后是几十年的技术累积与数不尽的实现细节,面对着眼前的数座大山,我们难道要像一个懦弱者一样东推西阻,畏缩不前?
我想技术这条路从某种角度来讲确实是枯燥的,乏味的,这也意味着不是所有人都可以数十年如一日的在这片属于自由者的理想国深耕。想要取得些许果实,唯有热情,努力与持之以恒。
很幸运XiyouLinuxGroup聚集着这样一群人。
博学之,审问之,慎思之,明辨之,笃行之。如是而已。

参考链接:
2018 Linux兴趣小组免试题解析
2017 Linux兴趣小组免试题解析
2016 Linux兴趣小组免试题解析
2015 Linux兴趣小组免试题解析
2014 Linux兴趣小组免试题解析
2013 Linux兴趣小组免试题解析