图的存储结构
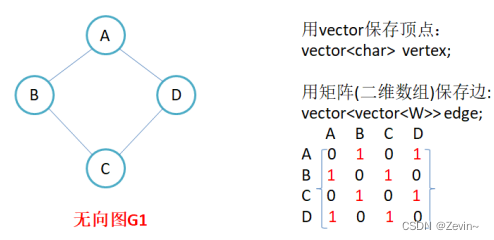
邻接矩阵
边和边之间关系通过矩阵数组来保存关系
- 邻接矩阵适合稠密图(复杂的顶点关系)
- 邻接矩阵可以O(1)判断顶点的连接关系
- 不适合查看一个顶点连接的所有边O(N)
A,B之间相连所以matrix[A][B]=1
template <class V, class W, W MAX_W = INT32_MAX, bool Direct = false>
class Graph
{
typedef Graph<V, W, MAX_W, Direct> Self;
private:
vector<V> _vertex; // 保存顶点
map<V, int> _indexmap; // 顶点映射下标的关系
vector<vector<W>> _matrix; // 邻接矩阵来保存边的数据,邻接矩阵适合稠密的关系图
public:
// 图的创建
// 1.IO输入
// 2.图结构写到文件中
// 3. 手动添加边
Graph() = default;
Graph(const V *a, size_t n)
{
_vertex.reserve(n);
for (size_t i = 0; i < n; i++)
{
_vertex.push_back(a[i]);
_indexmap[a[i]] = i;
}
_matrix.resize(n);
for (size_t i = 0; i < n; i++)
{
_matrix[i].resize(n, MAX_W);
}
}
// 获得顶点的下标
size_t GetVertexIndex(const V &v)
{
auto it = _indexmap.find(v);
if (it != _indexmap.end())
{
return it->second;
}
else
{
throw invalid_argument("顶点不存在");
return -1; // 防止编译器的优化
}
}
void AddEdge(const V &src, const V &dst, const W &w) // 添加边
{
// 添加边
size_t srci = GetVertexIndex(src);
size_t dsti = GetVertexIndex(dst);
_matrix[srci][dsti] = w;
if (Direct == false)
{
// 无相图,两边都要添加
_matrix[dsti][srci] = w;
}
}
邻接表
邻接表:使用数组表示顶点的集合,使用链表来表示边的关系
类似hashtable
- 适合稀疏的图(顶点之间关系比较简单)
- 方便查找一个节点的所有边
- 不适合判断两个节点之间是否相连

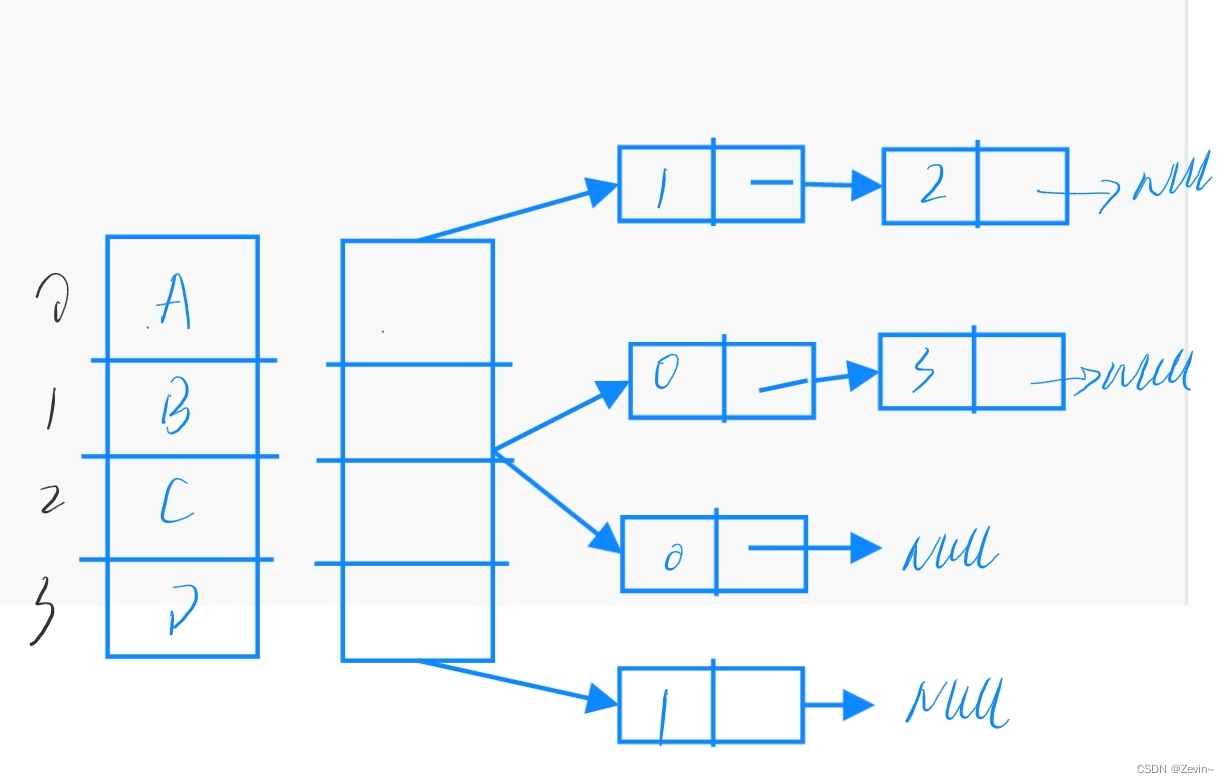
添加边关系:通过src顶点找到对应的数组,进行
头插元素来进行添加边
template <class W>
struct Edge
{
W _w;
int _dsti; // 目标点连接的下标
Edge<W> *_next;
Edge(W w, int dsti)
: _w(w), _dsti(dsti), _next(nullptr)
{
}
};
template <class V, class W, bool Direct = false>
class Graph
{
typedef Table::Edge<W> Edge;
private:
vector<V> _vertex; // 保存顶点
map<V, int> _indexmap; // 顶点映射下标的关系
vector<Edge *> _table; // 邻接表来保存边的数据,邻接矩阵适合稀疏的关系图,类似哈希
public:
// 图的创建
// 1.IO输入
// 2.图结构写到文件中
// 3. 手动添加边
Graph(const V *a, size_t n)
{
_vertex.reserve(n);
for (size_t i = 0; i < n; i++)
{
_vertex.push_back(a[i]);
_indexmap[a[i]] = i;
}
_table.resize(n, nullptr);
}
// 获得顶点的下标
size_t GetVertexIndex(const V &v)
{
auto it = _indexmap.find(v);
if (it != _indexmap.end())
{
return it->second;
}
else
{
throw invalid_argument("顶点不存在");
return -1; // 防止编译器的优化
}
}
void AddEdge(const V &src, const V &dst, const W &w) // 添加边
{
// 添加边
size_t srci = GetVertexIndex(src);
size_t dsti = GetVertexIndex(dst);
Edge *eg = new Edge(w, dsti); // 头插
eg->_next = _table[srci];
_table[srci] = eg;
// 如果是一个无相图
if (Direct == false)
{
Edge *eg = new Edge(w, srci); // 头插
eg->_next = _table[dsti];
_table[dsti] = eg;
}
}
图的遍历
DFS
DFS:深度优先搜索:先往深处遍历,深处遍历完了再回溯,查看上层未边俩的元素
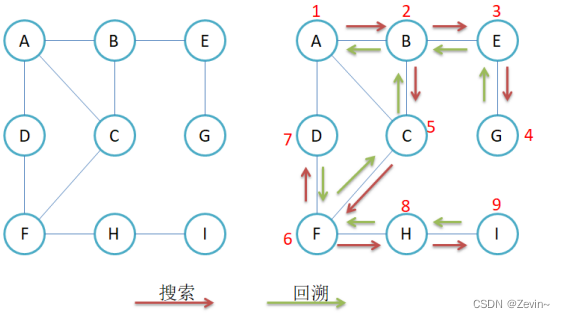
使用一个
visited数组,来标记元素访问与否,用递归来进行遍历
void _DFS(size_t srci, vector<bool> &visited)
{
visited[srci] = true;
cout << srci << ":" << _vertex[srci] << " ";
for (int i = 0; i < _vertex.size(); i++)
{
if (_matrix[srci][i] != MAX_W && visited[i] == false)
{
// 没有被访问过
_DFS(i, visited);
}
}
return;
}
void DFS(const V &src) // 深度遍历,
{
size_t srci = GetVertexIndex(src);
vector<bool> visited(_vertex.size(), false);
_DFS(srci, visited);
}
BFS
BFS:广度优先搜索,一层一层的遍历元素,直到遍历到最后一层的元素
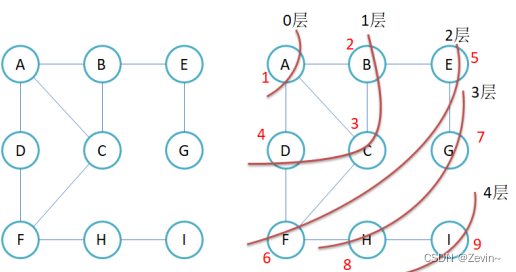
思路
使用一个队列和一个visited数组,元素入队列的时候,标记他对应的visited数组=true,元素出队列的时候,代入他连接的未入队列的所有节点,直到队列为空,遍历结束
// 确认两个点是否相连
// 遍历都是遍历顶点而不是遍历边
// 图的遍历,深搜:优先往深走
// 广搜:类似层序遍历
void BFS(const V &src) // 深度优先搜索
{
int srci = GetVertexIndex(src);
queue<int> q; // 队列进行搜索
q.push(srci);
vector<bool> visited(_vertex.size(), false); // 标记数组,入队列的时候就进行标记
visited[srci] = true;
int levelsize = 1;
while (!q.empty())
{
for (int i = 0; i < levelsize; i++) // 控制层序遍历
{
int front = q.front();
q.pop();
// 获得对头的所有的链接的元素
cout << front << ":" << _vertex[front] << " ";
for (size_t i = 0; i < _vertex.size(); i++)
{
if (_matrix[front][i] != MAX_W)
{
// 入队列
if (visited[i] == false) // 没被访问过,就要入队列
{
q.push(i); // 检查是否被标记了
visited[i] = true;
}
}
}
}
cout << endl;
levelsize = q.size();
}
}
最小生成树
构成最小生成树的原则
- 只能使用图中的边来构成最小生成树
- 只能使用n-1条边来连接图中的n个顶点
- 选用的n-1边不能构成回路
Kruskal
全局贪心的方法,每次在全局查找最小的边,同时判断这个边连接的两个顶点是否会形成环,如果不会形成环,就添加到最小生成树中
struct Edge
{
size_t _srci;
size_t _dsti;
W _w;
Edge(size_t srci, size_t dsti, W w)
: _srci(srci), _dsti(dsti), _w(w)
{
}
// 我们要重新弄一下比较函数
bool operator>(const Edge &e) const // 重载一下>函数
{
return _w > e._w;
}
};
// Kruskal 是每次都选出最小的边,然后保证选出的边不会成环即可,在全局选择最小
W Kruskal(Self &mintree) // 计算最小生成树
{
mintree._vertex = _vertex;
mintree._indexmap = _indexmap;
mintree._matrix.resize(_vertex.size());
for (size_t i = 0; i < _vertex.size(); i++)
{
mintree._matrix[i].resize(_vertex.size(), MAX_W);
}
priority_queue<Edge, vector<Edge>, greater<Edge>> pq; // 建立一个小堆
for (size_t i = 0; i < _vertex.size(); i++)
{
for (size_t j = 0; j < _vertex.size(); j++)
{
if (i < j && _matrix[i][j] != MAX_W) // 无相图,只要走一半即可
{
// 合法
Edge e(i, j, _matrix[i][j]);
pq.push(e);
}
}
}
// 依次选出最小的边,然后依次添加就可以了
// n个顶点,选出n-1条边
W total = W();
int n = _vertex.size();
int size = 0;
ufs2::UnionFindSet ufs(n); // 使用并查集来判断选中的点是否形成了一个环路
while (!pq.empty())
{
Edge min = pq.top(); // 最顶部的就是最小的边
pq.pop();
if (!ufs.Inset(min._dsti, min._srci))
{
// 这两个点不在一个集合,说明这两个点可以添加,连接起来
cout << _vertex[min._dsti] << "-" << _vertex[min._srci] << "->" << min._w << endl;
mintree.AddEdge(_vertex[min._srci], _vertex[min._dsti], min._w);
ufs.Union(min._dsti, min._srci);
++size;
total += min._w;
}
}
if (size == n - 1)
{
// 成功选出了n-1条边
//
return total;
}
else
// 可能出现走完没有选出的情况
return W();
}
Prim
局部贪心的方法,通过已经进入最小生成树的顶点和未进入最小生成树的顶点中,查找最小的边
通过优先级队列来记录所有已经进入树中延伸出去的所有边,每次查找里面最小的边,找到了判断是否已经在树中,如果已经在了,说明成环了,就继续,没有成环就添加入树中,同时把该顶点未添加到树中的所有边添加入队列中,进行下一次遍历
// Prim算法计算最小生成树算法
// 在已经连接点的集合和未连接点的集合中选出最小的边顶点,
// 局部贪心
W Prim(Self &mintree, const V &src)
{
int n = _vertex.size();
int srci = GetVertexIndex(src);
mintree._vertex = _vertex;
mintree._indexmap = _indexmap;
mintree._matrix.resize(_vertex.size());
for (size_t i = 0; i < _vertex.size(); i++)
{
mintree._matrix[i].resize(_vertex.size(), MAX_W);
}
//
// set<int> X; // 两个集合
// set<int> Y;
// X.insert(srci); // 先存进去一个起点
// for (size_t i = 0; i < n; i++)
// {
// if (i != srci)
// {
// Y.insert(i); // Y集合不存起点
// }
// }
vector<bool> X(n, false);
vector<bool> Y(n, true);
X[srci] = true;
Y[srci] = false;
// 从X到Y集合中,连接的边选出最小的边
priority_queue<Edge, vector<Edge>, greater<Edge>> minq; // 选出最小边
// 先把srci连接的边添加到队列中
for (size_t i = 0; i < n; i++)
{
if (_matrix[srci][i] != MAX_W)
{
// 合法的边
minq.push(Edge(srci, i, _matrix[srci][i]));
}
}
int size = 0;
W total = W();
while (!minq.empty())
{
Edge min = minq.top(); // 选出最小的边
minq.pop();
if (X[min._dsti]) // 如果选出的边都在X集合,或者都在Y集合就成环了
{
// 都为true,说明就成环了,起点一定是在X集合中的
// 成环了
continue;
}
mintree.AddEdge(_vertex[min._srci], _vertex[min._dsti], min._w);
// X.insert(min._dsti); // X集合添加一个元素
// Y.erase(min._dsti); // Y集合减少这个元素
X[min._dsti] = true;
Y[min._dsti] = false;
size++;
total += min._w;
if (size == n - 1)
{
break;
}
// 把新添加进来的所有边都过一遍,
for (size_t i = 0; i < n; i++)
{
if (_matrix[min._dsti][i] != MAX_W && Y[i]) // 新添加到队列里面,要保证添加的点并不已经在集合中了
{
// 目标点要在Y集合
// 合法的边
minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));
}
}
}
if (size == n - 1)
{
// 成功选出了n-1条边
//
return total;
}
else
// 可能出现走完没有选出的情况
return W();
}
最短路径
在带权有相图G中的某个顶点出发,找到通往另一个顶点的最短路径,最短也就是路径的权值总和最短
Djkstra
单源最短路径:一个源顶点到每个顶点之间的最短路径
如源顶点为S,图中的顶点有A,B,C,D
计算S-D,S-B,S-A,S-C这些路径的最短路径
使用一个dist数组来记录最小路径,ppath来记录自己的父亲是谁
从一个已经确定最小路径进行查找他延伸出去的边,进行更性这些顶点的路径最小值
// 打印最短路径的算法
void Dijkstra(const V &src, vector<W> &dist, vector<int> &pPath)
{
size_t srci = GetVertexIndex(src);
size_t n = _vertex.size();
dist.resize(n, MAX_W); // 一开始这个距离就初始化给一个最大值
pPath.resize(n, -1); // 父路径
// 自己到自己的距离就设置为0即可
dist[srci] = 0;
// 自己的父亲路径就是自己
pPath[srci] = srci;
vector<bool> s(n, false); // 已经确定最短路径的顶点集合
// 如果所有的点都被更新一遍了,就结束了,需要更新n次
for (int j = 0; j < n; j++)
{
// 去选最短路径的顶点来进行更新
int u = 0;
W min = MAX_W; // 最小的权值
for (size_t i = 0; i < n; i++)
{
if (s[i] == false && dist[i] < min) // dist[i]已经被操作了,已经小于min了,但是他还不是已经确定的了的点
{
u = i; // u保存哪一个需要接下来进行被操作
min = dist[i]; // 保存此时的最小值
}
}
s[u] = true;
// 进行松弛操作
// 更新u链接的顶点v,就可以更新
for (size_t v = 0; v < n; v++)
{
//保证v这个点没有更新过
if (s[v]==false&&_matrix[u][v] != MAX_W && dist[u] + _matrix[u][v] < dist[v]) // 记录u链接除去的所有边
{
// 如果此时链接出去的点小于原来记录 的值,那么我们就需要进行更新
dist[v] = dist[u] + _matrix[u][v]; // 更新路径中的值
pPath[v] = u; // 记录我们的父亲为u
}
}
}
}