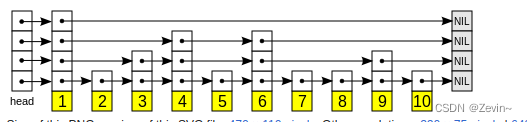
跳表概念

跳表（Skip List）是一种基于链表实现的数据结构，它允许快速地查找、插入和删除元素，时间复杂度为 O(log n)。
跳表通过在链表中建立多级索引来实现快速查找。每一级索引中的元素都是前一级索引中元素的子集，最高级索引包含所有元素。通过跳过一些元素，跳表可以快速地定位到需要查找的元素，从而提高了查找的效率。
跳表的实现相对简单，而且可以支持并发操作，因此在实际应用中被广泛使用，比如 Redis 中就使用了跳表来实现有序集合。

在这里插入图片描述

跳表的优点

相比数组，跳表有以下优点：

插入和删除操作更高效：在跳表中，插入和删除操作的时间复杂度是O(log n)，而在数组中，这些操作的时间复杂度是O(n)。
支持快速查找：跳表中的元素是有序的，可以使用二分查找的方式快速定位元素，时间复杂度是O(log n)。而在数组中，查找元素的时间复杂度是O(n)。
支持高效的区间操作：跳表中的元素是有序的，因此支持高效的区间操作，比如查找某个区间内的元素，时间复杂度是O(log n+k)，其中k是区间内的元素个数。而在数组中，这些操作的时间复杂度是O(n)。
跳表支持高效的区间操作，可以使用以下方式实现：
1. 定位到区间的起始元素：从最高级索引开始，逐级向下遍历跳表，找到第一个大于或等于区间起始值的元素。
  2.顺序遍历区间内的元素：从起始元素开始，顺序遍历跳表中的元素，直到找到大于区间终止值的元素为止，或者遍历到跳表的末尾。
2. 将遍历到的元素加入结果集：在遍历区间内的元素时，将遍历到的元素加入结果集中。
支持并发操作：跳表的结构可以支持并发操作，多个线程可以同时对跳表进行读操作，而不需要加锁。而在数组中，多个线程同时对数组进行读写操作可能会导致数据不一致的问题，需要加锁保证线程安全。

模拟实现

#pragma once
#include <iostream>
using namespace std;
#include <vector>
#include <ctime>
#include <cstdlib>
#include <cmath>
#include <unordered_set>
class skipList
{
   
private:
    struct Node
    {
   
        int key;
        vector<Node *> next; //每一层对应的next数组
        Node(int _key, size_t level_)
            : key(_key), next(level_, nullptr) // level层，每一层都是nullptr
        {
   
        }
    };

private:
    size_t _level; //当前的层数这个是我们规定的最大层数
    Node *_head;   //跳表的头节点，每一层都需要有一个这个头节点

public:
    skipList(size_t level = 4)
        : _level(level)
    {
   
        _head = new Node(-1, level); //每个都设置为-1,有level层,头节点，先初始化成-1,我们再进行添加
    }

    size_t randomLevel() //获得一个随机的层数
    {
   
        size_t level = 1; //这里规定第1层就是最底下的那一层索引层
        while (rand() % 2)
        {
   
            level++;
        }
        //如果获得的level比最大层还大的话，就返回最大层，否则就返回这个单前层数
        return level > _level ? _level : level; //在插入的时候判断最高应该在哪一个层
    }

    bool search(int key)
    {
   
        Node *cur = _head;
        for (int i = _level - 1; i >= 0; i--) //从最上层，下层到最下层

        {
   
            while (cur->next[i] != nullptr && cur->next[i]->key < key)
            {
   
                cur = cur->next[i];
            }
            if (cur->next[i] != nullptr && cur->next[i]->key == key) //这个地方找到了
            {
   
                return true; //在里面找到了对应的节点就成功
            }
        }
        return false; //都没找到，就返回失败
    }
    void insert(int key) //添加一层
    {
   
        size_t level = randomLevel();      //随机获得一个层数
        Node *node = new Node(key, level); //这个就是根据获得的随机层来进行操作
        Node *cur = _head;
        for (int i = _level - 1; i >= 0; i--) //从最高层开始找
        {
   
            while (cur->next[i] != nullptr && cur->next[i]->key < key)
            {
   
                // cur当前层的下一个节点存在，且小于需要的key，我们就需要继续往后
                cur = cur->next[i];
            }
            //这个地方就要么等于k，要么大于k
            if (level > i) //这个地方的level是我们自己随机获得的一个层数，我们要求是level以下都要建立索引
            {
   
                //插入节点
                node->next[i] = cur->next[i];
                cur->next[i] = node;
            }
        }
    }
    bool earse(int key)
    {
   
        //这个如果key有多个层，每个层都要进行删除
        Node *cur = _head;
        Node *node = nullptr;
        for (int i = _level - 1; i >= 0; i--)
        {
   
            while (cur->next[i] != nullptr && cur->next[i]->key < key) //在同一层往后迭代
            {
   
                cur = cur->next[i];
            }
            if (cur->next[i] != nullptr && cur->next[i]->key == key) //现在操作的都是范围节点的前一个节点
            {
   
                //这个就是找到了对应节点
                //要把从这一层开始的所有的该节点都要断开连接
                node = cur->next[i];          //这个地方的node就是我们需要删除的节点
                cur->next[i] = node->next[i]; //这样就删除这一层,继续下层
            }
        }
        if (node == nullptr)
        {
   
            return false;
        }
        else
        {
   
            delete node;
            node = nullptr;
            return true;
        }
    }
    vector<int> rangeSearch(int key1, int key2)
    {
   
        vector<int> result; //返回的结果
        Node *cur = _head;
        for (int i = _level - 1; i >= 0; i--)//这个先往后找，并下层到对应的大于key1的位置
        {
   
            while (cur->next[i] != nullptr && cur->next[i]->key < key1) //先一直往后找，找到比当前还要大的位置
            {
   
                cur = cur->next[i];
            }
            //直接下层到最后一层
        }
        //下层到了对应的位置，我们就进行在底层的一个顺序遍历即可
        
        if (cur->next[0] != nullptr && cur->next[0]->key >= key1) //如果当前节点比这个key还要大，我们就需要在这个节点后面进行遍历
        {
   
            Node *node = cur->next[0];                   //获得对应的node
            while (node != nullptr && node->key <= key2) //如果这个node小于key2说明范围查找成功
            {
   
                result.push_back(node->key);
                node = node->next[0];
            }
        }
        return result;
    }

    void printSkipList() //打印链表
    {
   
        for (int i = _level - 1; i >= 0; i--)
        {
   
            Node *cur = _head;
            while (cur->next[0] != nullptr)
            {
   
                if (cur->next.size() > i) //如果他的next的层数比i大
                {
   
                    cout << cur->next[0]->key << "\t";
                }
                else
                {
   
                    cout << "\t";
                }
                cur = cur->next[0];
            }
            cout << endl;
        }
    }
};