图论（BFS）

原 作者 张敏睿 | 发表于 | 分类于 2022级

目录

BFS

适用场景

  • 解决两个点之间的最短路径问题：迷宫问题
  • 和DFS都能解决的问题：岛屿问题

迷宫问题模板

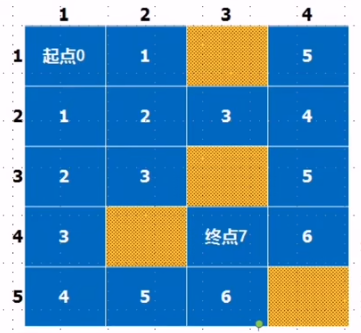
在这里插入图片描述


算法：
1. 将起点入队
2. 队首结点可拓展的点入队，如果没有可拓展的点，将队首结点出队
3. 重复步骤，直到达到目标位置或者队列为空

  • 注意点：当一个点加入队列了，就代表该点已被访问，需要进行标记（而非从队列里拿出来时再进行标记）
#include <iostream>
#include <queue>
using namespace std;

int a[100][100];  // 各位置信息（是否有路径）
int v[100][100];  // 标记某个位置是否被访问过（1有0无）
struct point {
   
    int x;
    int y;
    int step;
};                          // 队列里每个元素
queue<point> r;             // 申请队列
int dx[4] = {
   1, 0, -1, 0};  // 向四个方向延伸，顺序为：右 下 左 上
int dy[4] = {
   0, -1, 0, 1};
int flag = 0;  // 是否到达终点

int main() {
   
    // 数据输入
    int n, m, startx, starty, endx, endy;
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i++) {
    
        for (int j = 1; j <= m; j++) {
   
            scanf("%d", &a[i][j]);//1为路径，2为墙
        }
    }
    scanf("%d %d %d %d", &startx, &starty, &endx,
          &endy);  // 输入起点坐标和终点坐标

    // BFS
    point start;
    start.x = startx;
    start.y = starty;
    start.step = 0;
    r.push(start);          // 将起点坐标入队
    v[startx][starty] = 1;  // 将该点标记为已访问

    while (!r.empty()) {
   
        int x = r.front().x;  // 取队首元素的x坐标
        int y = r.front().y;  // 取队首元素的y坐标
        int step = r.front().step;
        printf("%d %d %d\n",x,y,step);

        if (x == endx && y == endy) {
     // 到达终点了
            flag = 1;
            printf("%d\n", step);
            break;
        }

        for (int k = 0; k <= 3; k++) {
     // 向四个方向拓展
            int newx, newy;
            newx = x + dx[k];
            newy = y + dy[k];
            if (a[newx][newy] == 1 &&
                v[newx][newy] == 0)  // 该拓展点可以被访问且未被访问过
            {
   
                point newpoint;
                newpoint.x = newx;
                newpoint.y = newy;
                newpoint.step = step+1;
                r.push(newpoint);  // 新拓展点入队
                v[newx][newy] = 1;
            }
        }
        r.pop();  // 拓展完后将队首元素出队
    }

    if (flag == 1) {
   
        printf("找到路径");
    } else {
   
        printf("未找到路径");
    }

    return 0;
}

岛屿数量模板

class Solution {
   
private:
int dir[4][2] = {
   0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
   
    queue<pair<int, int>> que;
    que.push({
   x, y});
    visited[x][y] = true; // 只要加入队列，立刻标记
    while(!que.empty()) {
   
        pair<int ,int> cur = que.front(); que.pop();
        int curx = cur.first;
        int cury = cur.second;
        for (int i = 0; i < 4; i++) {
   
            int nextx = curx + dir[i][0];
            int nexty = cury + dir[i][1];
            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 越界了，直接跳过
            if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
   
                que.push({
   nextx, nexty});
                visited[nextx][nexty] = true; // 只要加入队列立刻标记
            }
        }
    }
}
public:
    int numIslands(vector<vector<char>>& grid) {
   
        int n = grid.size(), m = grid[0].size();
        vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));

        int result = 0;
        for (int i = 0; i < n; i++) {
   
            for (int j = 0; j < m; j++) {
   
                if (!visited[i][j] && grid[i][j] == '1') {
   
                    result++; // 遇到没访问过的陆地，+1
                    bfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
                }
            }
        }
        return result;
    }
};

例题

腐烂的橘子

特点：多个起点，且起点已告知，同时开始
解决：把起点都push到队列里面去
题：
在这里插入图片描述

struct point {
   
    int x;
    int y;
    int step;
};                          // 队列里每个元素
queue<point> r;             // 申请队列
int dx[4] = {
   1, 0, -1, 0};  // 向四个方向延伸，顺序为：右 下 左 上
int dy[4] = {
   0, -1, 0, 1};
int v[10][10]; 
int INF = 10000;

class Solution {
   
   public:
    int orangesRotting(vector<vector<int>>& grid) {
   
        // 找腐烂的橘子
        int startx, starty;
        for (int i = 0; i < grid.size(); i++) {
   
            for (int j = 0; j < grid[i].size(); j++) {
   
                if (grid[i][j] == 2) {
   
                    v[i][j] = 0;  // 腐烂橘子腐烂的时间为0
                    point t;
                    t.x = i;
                    t.y = j;
                    t.step = 0;
                    r.push(t);  // 把烂橘子全部放到队列里去
                } else if (grid[i][j] == 1) {
   
                    v[i][j] = INF;  // 新鲜橘子腐烂时间要开始为无穷大
                } else {
   
                    v[i][j] = -1;  // 空位不会腐烂
                }
            }
        }

        // BFS
        while (!r.empty()) {
   
            int x = r.front().x;  // 取队首元素的x坐标
            int y = r.front().y;  // 取队首元素的y坐标
            int step = r.front().step;

            for (int k = 0; k <= 3; k++) {
     // 向四个方向拓展
                int newx, newy;
                newx = x + dx[k];
                newy = y + dy[k];
                
                if(newx<0||newx>=grid.size()||newy<0||newy>=grid[0].size()){
    // 新拓展点越界了
                    continue;
                }
                
                if (v[newx][newy] != -1 && v[newx][newy] != 0) {
     // 该拓展点有橘子且未被访问过
                    point newpoint;
                    newpoint.x = newx;
                    newpoint.y = newy;
                    newpoint.step = step + 1;

                    if (newpoint.step <= v[newx][newy]) {
   
                        v[newx][newy] = newpoint.step;
                        r.push(newpoint);  // 新拓展点入队
                    }
                }
            }
            r.pop();  // 拓展完后将队首元素出队
        }

        //寻找是否存在未腐烂的橘子 
        int max=0;
        for (int i = 0; i < grid.size(); i++) {
   
            for (int j = 0; j < grid[i].size(); j++) {
   
                if (v[i][j]>max) {
   
                    max = v[i][j];
                }
            }
        }
        if(max==INF){
   
            return -1;
        }else{
   
            return max;
        }
    }
};

岛屿数量

特点：多个起点，且起点未告知
解决：把一个起点遍历完后，再找其他起点进行遍历
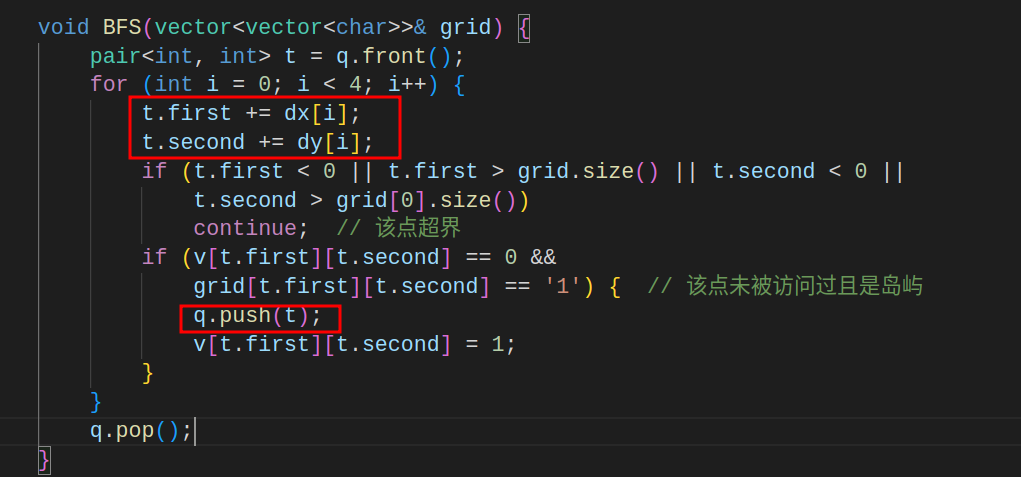
题：在这里插入图片描述

遇到的问题一：在这里插入图片描述

  • 由于在找出队点的附近点时，t的两个成员会随着for循环的进行而不断变大，这样新得到的点就离t点越来越远
  • 解决：每次用一个新的变量来存新的点的位置

遇到的问题二：
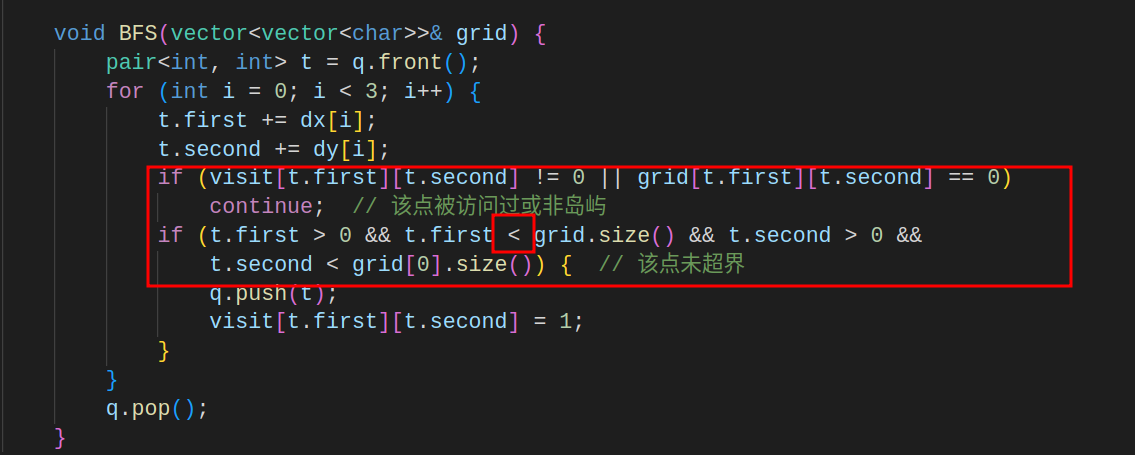
在这里插入图片描述

  • 如果t的两个成员的值已经超过grid的范围，此时再访问grid，将会造成堆缓冲区溢出
  • t.first < grid.size() ，当 t.first = grid.size() 时，也会造成访问越界
  • 解决：先判断t的两个成员值是否合法，t.first < grid.size() 改为t.first <= grid.size()
class Solution {
   
public:
    int numIslands(vector<vector<char>>& grid) {
   
        int num = 0; // 记录岛屿数量
        memset(v, 0, sizeof(v));
        pair<int, int> start = find(grid);
        if (start.first == -1)
            return 0;
        do {
   
            q.push(start);
            num++;
            v[start.first][start.second] = 1;

            while (!q.empty()) {
   
                BFS(grid);
            }

            start = find(grid);
        } while (start.first != -1);
        return num;
    }

private:
// 找起点（找岛屿位置）
    pair<int, int> find(vector<vector<char>>& grid) {
   
        for (int i = 0; i < grid.size(); i++) {
   
            for (int j = 0; j < grid[i].size(); j++) {
   
                if (grid[i][j] == '1' && v[i][j] == 0) {
    // 是陆地且未被访问过
                    return make_pair(i, j);
                }
            }
        }
        return make_pair(-1, -1); // 没找到
    }

// 对每个岛屿进行BFS
    void BFS(vector<vector<char>>& grid) {
   
        pair<int, int> newt, t = q.front();
        for (int i = 0; i < 4; i++) {
   
            newt.first = t.first + dx[i];
            newt.second = t.second + dy[i];
            if (newt.first < 0 || newt.first >= grid.size() ||
                newt.second < 0 || newt.second >= grid[0].size())
                continue; // 该点超界
            if (v[newt.first][newt.second] == 0 &&
                grid[newt.first][newt.second] ==
                    '1') {
    // 该点未被访问过且是岛屿
                q.push(newt);
                v[newt.first][newt.second] = 1;
            }
        }
        q.pop();
    }

    int v[300][300]; // 是否被访问过
    int dx[4] = {
   1, 0, -1, 0};
    int dy[4] = {
   0, 1, 0, -1};
    queue<pair<int, int>> q;
};

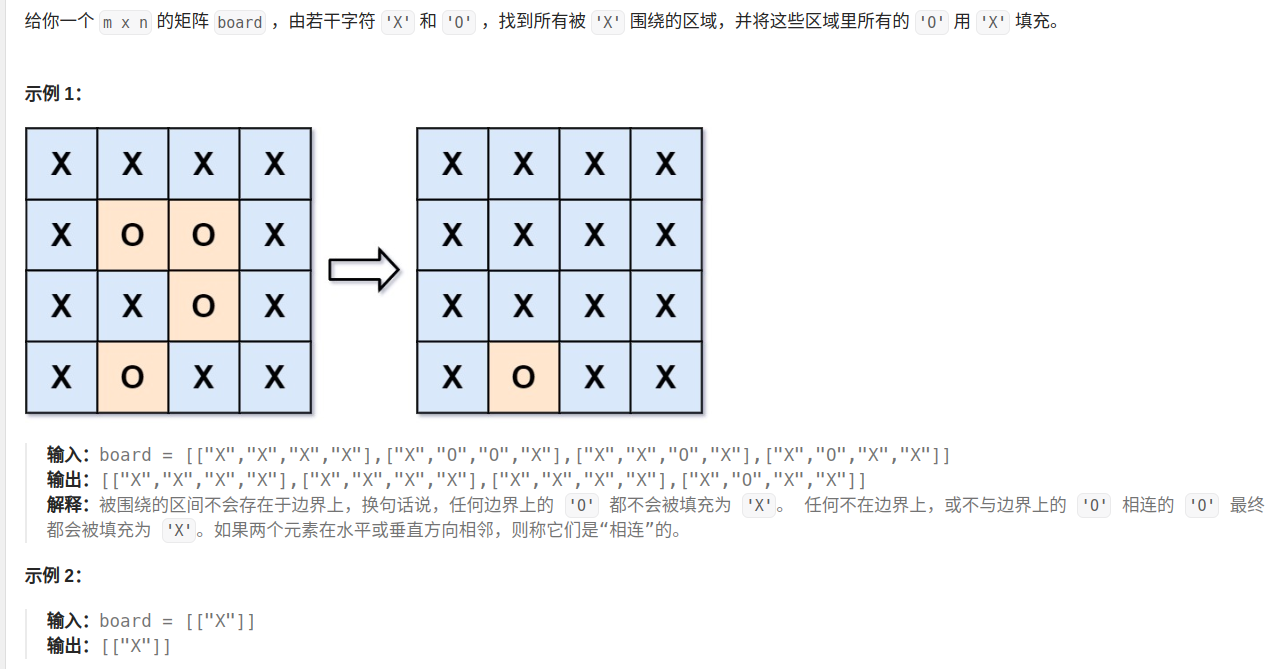
被围绕的区域

特点：多个起点，起点未知，理解为起点在边界，同时开始
解决：把起点（边界点）都push到队列里面去，BFS时把与边界两连的区域全部设为被访问，v[i][j]=1
最后没被访问过的就是被围绕的区域
题：在这里插入图片描述

class Solution {
   
   public:
    void solve(vector<vector<char>>& board) {
   
        memset(v, 0, sizeof(v));
        find(board);

        while (!q.empty()) {
   
            BFS(board);
        }

		//最后没被访问过的就是被围绕的区域
        for (int i = 0; i < board.size(); i++) {
   
            for (int j = 0; j < board[i].size(); j++) {
   
                if (board[i][j] == 'O' && v[i][j] == 0) {
   
                    board[i][j] = 'X';
                }
            }
        }
    }

   private:
   // 把起点（边界点）都push到队列里面去
    void find(vector<vector<char>>& board) {
   
        pair<int, int> point = make_pair(-1,-1);
        for (int i = 0; i < board.size(); i++) {
   
            for (int j = 0; j < board[i].size(); j++) {
   
                if (board[i][j] == 'O' && v[i][j] == 0)  // 是O且未被访问过
                    if (i == 0 || i == board.size() - 1 || j == 0 ||
                        j == board[0].size() - 1) {
     // 是边界
                        v[i][j] = 1;
                        point = make_pair(i, j);
                        q.push(point);
                    }
            }
        }
    }

	// BFS时把与边界两连的区域全部设为被访问，v[i][j]=1
    void BFS(vector<vector<char>>& board) {
   
        pair<int, int> newt, t = q.front();
        for (int i = 0; i < 4; i++) {
   
            newt.first = t.first + dx[i];
            newt.second = t.second + dy[i];
            if (newt.first < 0 || newt.first >= board.size() ||
                newt.second < 0 || newt.second >= board[0].size())
                continue;  // 该点超界
            if (v[newt.first][newt.second] == 0 &&
                board[newt.first][newt.second] ==
                    'O') {
     // 该点未被访问过且有O
                q.push(newt);
                v[newt.first][newt.second] = 1;
            }
        }
        q.pop();
    }

    int v[300][300];  // 是否被访问过
    int dx[4] = {
   1, 0, -1, 0};
    int dy[4] = {
   0, 1, 0, -1};
    queue<pair<int, int>> q;
};

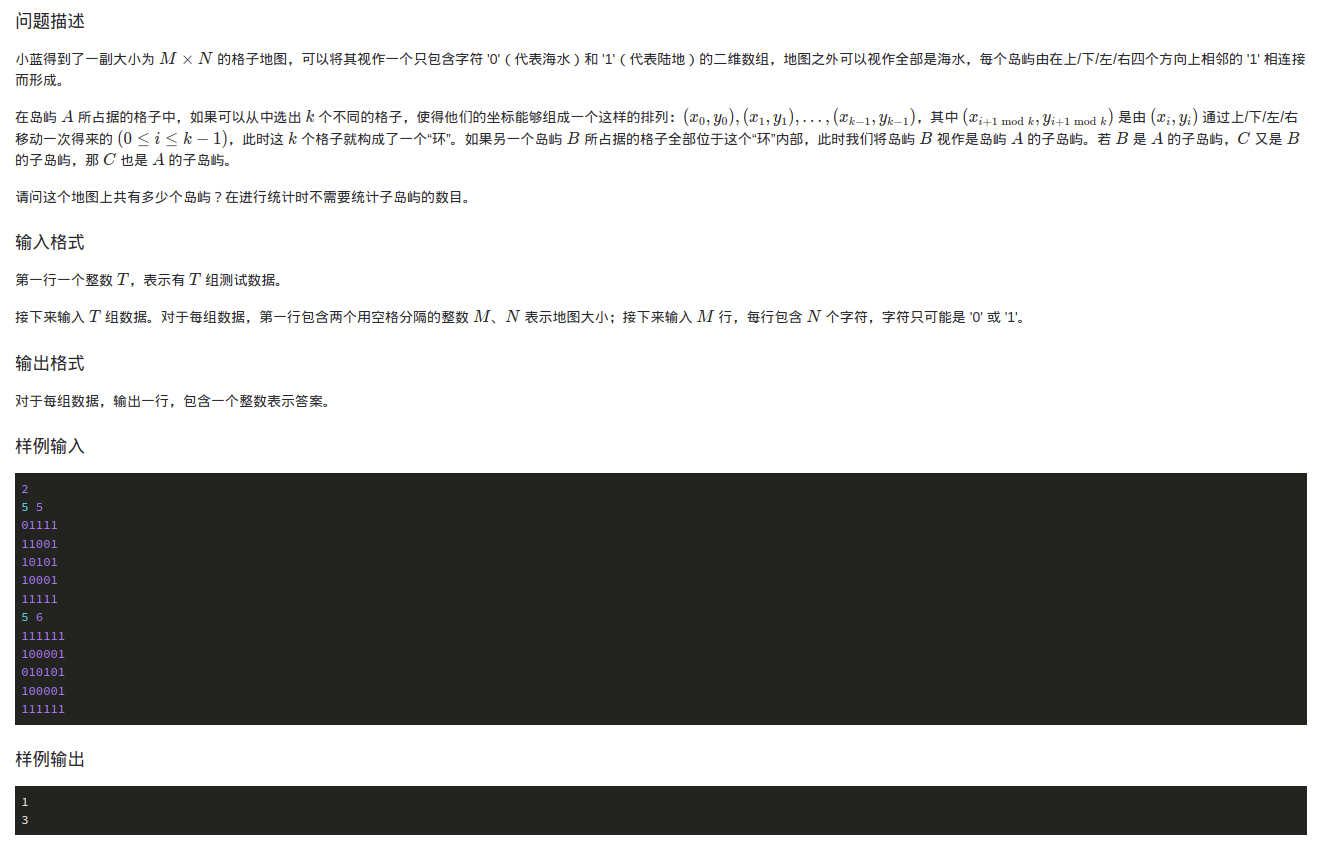
蓝桥_岛屿的个数—>当模板

特点：有的岛屿内部有子岛屿,子岛屿不算数
解决：

  • 首先我们用一个比地图大一圈的矩阵来存储这个地图（只需要大一圈就行，方便对地图的操作）
    由于地图外都是海水，所以所有点都初始化为字符 ‘0’
  • 从 (0,0)开始把所有相连的海水都标记为2（第一次DFS，搜索时考虑八连通），图中所有剩下没有被更改的 ‘0’ 一定在岛屿内部
  • 遍历一遍地图，把所有 ‘0’ 都变成 ‘1’，这样岛屿和其内部的子岛屿就 “合为一体” 了
  • 剩下的就是第一步对应的问题（第二次DFS，搜索时考虑四连通）

题：
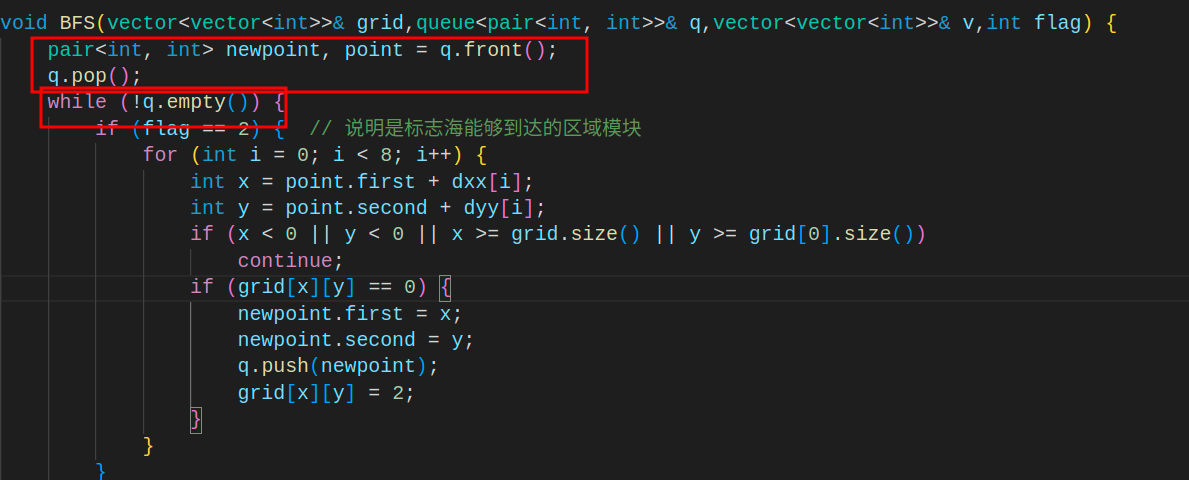
在这里插入图片描述

遇到的问题:
在这里插入图片描述

  • 本身函数参数的队列q就只有一个元素,结果BFS一开始就把唯一的元素给pop了,导致队列为空,进而无法进入while循环
  • 解决: 把取元素和出队放到while循环里面的最开始的地方

对于要自己关注输入的题来说:
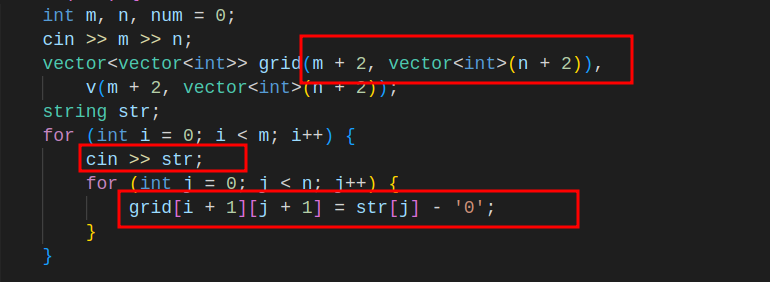
在这里插入图片描述

  • grid初始化时要给大小
    • 如:vector<vector<int>> grid(m, vector<int>(n))
  • 由于给的数据是一整行,所以用string类型的进行整行读入,再一个一个放入grid中
    • 注意:grid[i][j] = str[j] - '0' 要进行减去一个'0'
#include <bits/stdc++.h>
using namespace std;

int dx[4] = {
   1, 0, -1, 0};
int dy[4] = {
   0, 1, 0, -1};
int dxx[8] = {
   1, 1, 0, -1, -1, -1, 0, 1};
int dyy[8] = {
   0, 1, 1, 1, 0, -1, -1, -1};

void BFS(vector<vector<int>>& grid,queue<pair<int, int>>& q,vector<vector<int>>& v,int flag) {
   
    while (!q.empty()) {
   
        pair<int, int> newpoint, point = q.front();
        q.pop();
        if (flag == 2) {
     // 说明是标志海能够到达的区域模块
            for (int i = 0; i < 8; i++) {
   
                int x = point.first + dxx[i];
                int y = point.second + dyy[i];
                if (x < 0 || y < 0 || x >= grid.size() || y >= grid[0].size())
                    continue;
                if (grid[x][y] == 0) {
   
                    newpoint.first = x;
                    newpoint.second = y;
                    q.push(newpoint);
                    grid[x][y] = 2;
                }
            }
        }
        if (flag == 1) {
     // 说明是统计岛屿个数模块
            for (int i = 0; i < 4; i++) {
   
                int x = point.first + dx[i];
                int y = point.second + dy[i];
                if (x < 0 || y < 0 || x >= grid.size() || y >= grid[0].size())
                    continue;
                if (grid[x][y] == 1 && v[x][y] == 0) {
   
                    newpoint.first = x;
                    newpoint.second = y;
                    q.push(newpoint);
                    v[x][y] = 1;
                }
            }
        }
    }
}

int main() {
   
    int t;
    cin >> t;
    while (t--) {
   
        int m, n, num = 0;
        cin >> m >> n;
        vector<vector<int>> grid(m + 2, vector<int>(n + 2)),v(m + 2, vector<int>(n + 2));
        string str;
        for (int i = 0; i < m; i++) {
   
            cin >> str;
            for (int j = 0; j < n; j++) {
   
                grid[i + 1][j + 1] = str[j] - '0';
            }
        }

        // 从00开始,通过八个方向遍历地图,把是0的地方全部设置为2,表示外部海水能到达的区域
        queue<pair<int, int>> q;
        pair<int, int> point(0, 0);
        q.push(point);
        BFS(grid, q, v, 2);

        // 遍历一次地图,把所有0变为1.这样内部的子岛屿就和外部的岛屿连到一起了
        for (int i = 0; i < m + 2; i++) {
   
            for (int j = 0; j < n + 2; j++) {
   
                if (grid[i][j] == 0)
                    grid[i][j] = 1;
            }
        }

        // 正常BFS,找岛屿的个数即可
        for (int i = 1; i <= n; i++) {
   
            for (int j = 1; j <= m; j++) {
   
                if (v[i][j] == 0 && grid[i][j] == 1) {
   
                    pair<int, int> point = make_pair(i, j);
                    q.push(point);
                    v[i][j] = 1;
                    num++;
                    BFS(grid, q, v, 1);
                }
            }
        }

        // 打印岛屿个数
        cout << num << endl;
    }
}

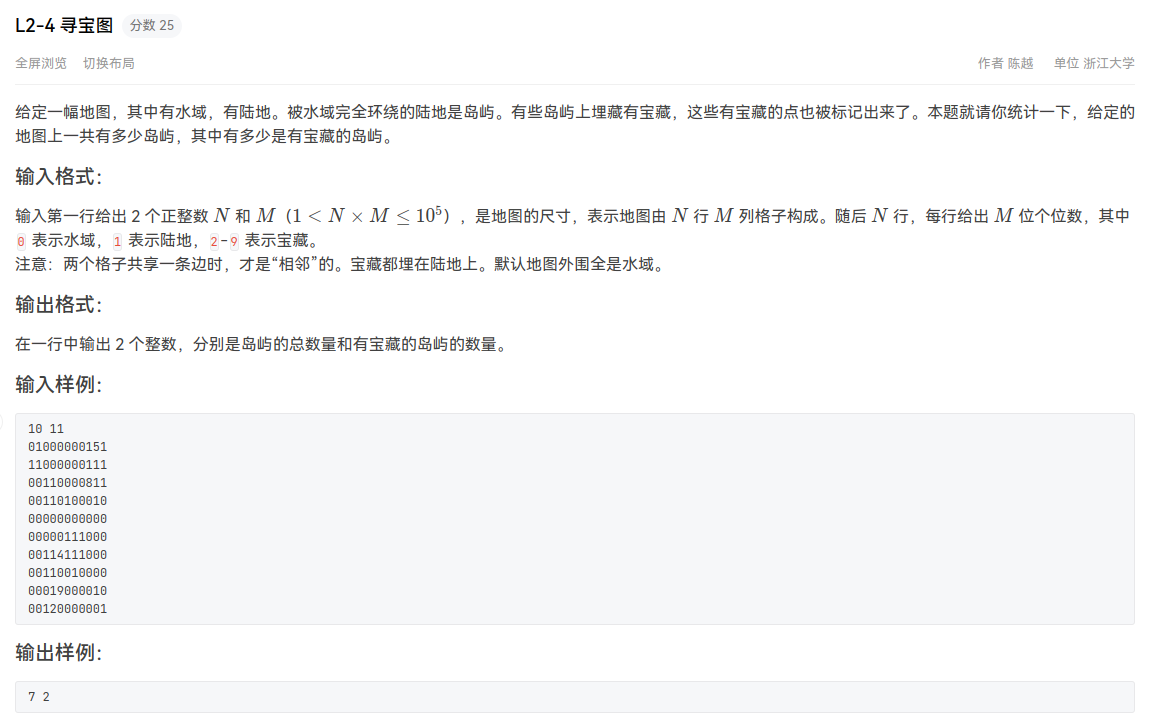
PTA_寻宝图—>上题模板的做法

特点：统计岛屿和宝藏岛屿的个数
解决：遇到有宝藏的岛屿时,标注一下
题：在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;

int dx[4] = {
   1,0,-1,0};
int dy[4] = {
   0,1,0,-1};

int BFS(vector<vector<int>> &grid,queue<pair<int,pair<int,int>>> &q,vector<vector<int>> &v)
{
   
    int flag = 0;
    while(!q.empty()){
   
        pair<int,pair<int,int>> newpoint,point = q.front();
        q.pop();
        if(point.second.second>1)
            flag = 1;//说明确实有宝藏

        for(int i=0;i<4;i++){
   
            int x = point.first + dx[i];
            int y = point.second.first + dy[i];
            if(x<0||y<0||x>=grid.size()||y>=grid[0].size())continue;
            if(v[x][y]==0&&grid[x][y]!=0){
   
                v[x][y] = 1;
                newpoint = make_pair(x,make_pair(y,grid[x][y]));
                q.push(newpoint);
            }
        }
    }
    return flag;
}

int main()
{
   
    int n,m,num = 0,velnum = 0;
    cin >> n >> m;
    vector<vector<int>> grid(n,vector<int>(m)),v(n,vector<int>(m));
    queue<pair<int,pair<int,int>>> q;
    for(int i=0;i<n;i++){
   
        string str;
        cin >> str;
        for(int j=0;j<m;j++){
   
            grid[i][j] = str[j]-'0';
        }
    }

    for(int i =0;i<n;i++)
    {
   
        for(int j=0;j<m;j++){
   
            if(v[i][j]==0&&grid[i][j]!=0){
   
                v[i][j]=1;
                pair<int,pair<int,int>> point = make_pair(i,make_pair(j,grid[i][j]));
                q.push(point);
                num ++ ;
                int flag = BFS(grid,q,v);
                if(flag == 1)velnum++;
            }
        }
    }

    cout << num << " " << velnum;
}

非规整图模板

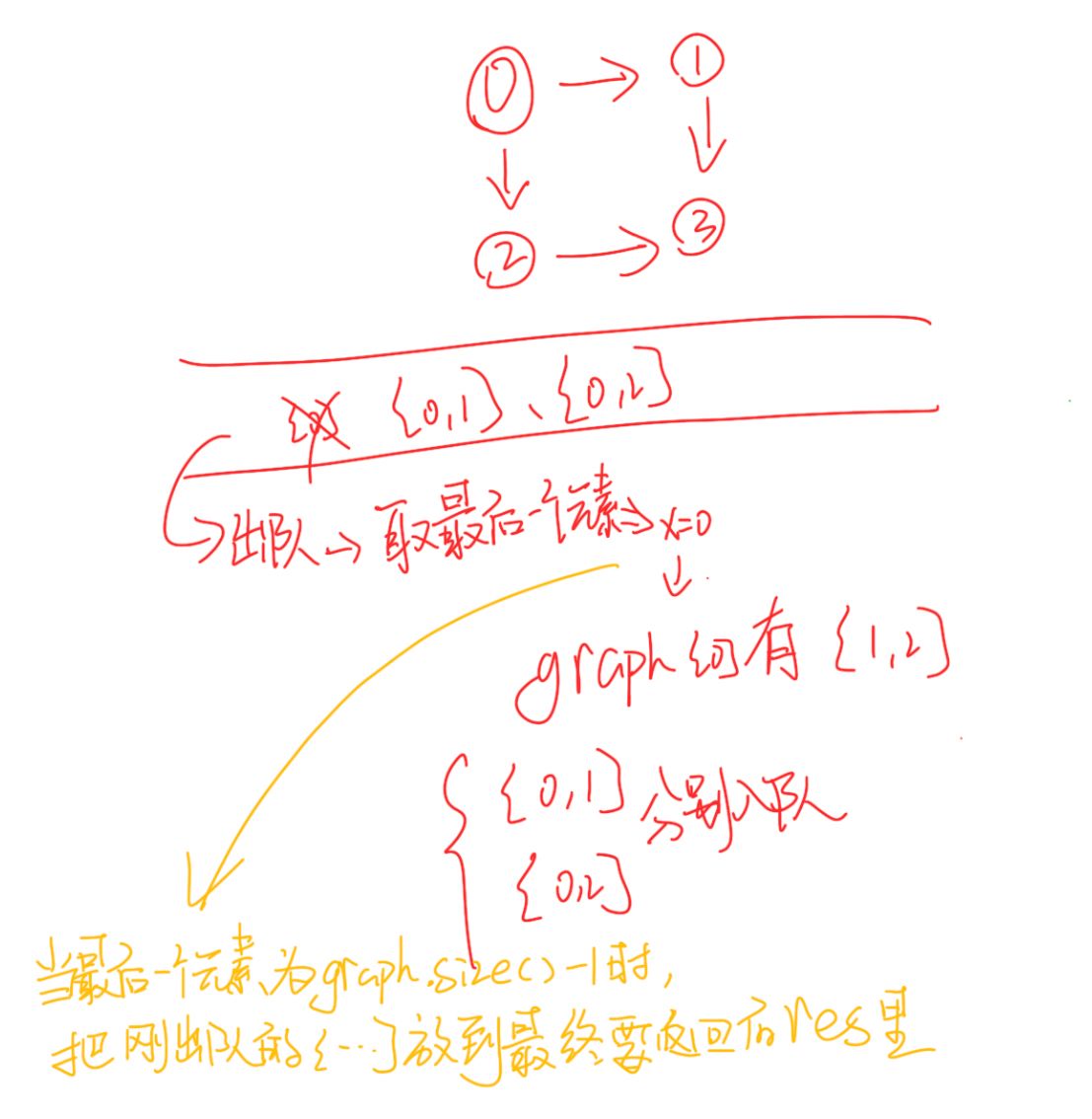
在这里插入图片描述在这里插入图片描述

class Solution {
   
   public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
   
        // BFS
        queue<vector<int>> q;
        vector<vector<int>> res;//存储ok的路径
        vector<int> road;
        road.push_back(0);
        q.push(road);
        while (!q.empty()) {
   
            vector<int> road = q.front();
            q.pop();
            int x = road.back();
            if(x == graph.size()-1){
   //这个路径的最后一个元素为终点，说明该路径ok
                res.push_back(road);
                continue;
            }
            for(int i=0;i<graph[x].size();i++){
   
                vector<int> newroad = road;
                newroad.push_back(graph[x][i]);
                q.push(newroad);
            }
        }
        return res;
    }
};